On Synergies of Schema Theory and Theory of Levels

Both Schenkerian analysis and schema theory focus on the music of the ‘long 18^th century’ and the melodic-contrapuntal aspects of compositional technique, including figured bass, linear and cadential patterns, and the art of diminution. Furthermore, they share the focus on the outer voices, the representation of notes by numbered scale degrees and the approach to reduce (or trace back) complex figures to simpler and more general ones.[1] On the other hand, their underlying theoretical concepts are quite different.[2] Schenkerian analysis accentuates the construction of functional relationships within an entire composition, while, in contrast, schema theory constructs very few relationships, but instead presents small-scale patterns and typical sequences of them as cognitively-anchored, historically-rooted, and socially-situated conventions.

Synergies and possible interactions of both approaches seem to me to be less in their partial similarities, but rather in the complementarity of the questions and issues they deal with. In some respects an informative Schenkerian graph represents its author’s tacit knowledge of schemata and style conventions.[3] On the other hand, the communicative strategies that schema theory deals with are based on implicit systematic and functional preconditions that have not yet been sufficiently reflected in this context.

I want to examine the extent to which the schema concept and the Schenkerian concept of hierarchical organized tonal structures may interlock or, at least, illuminate each other. Using specific examples, I will address this question in two parts.

Firstly, I compare three 16- to 30-bar pieces by Mozart and Haydn with significant similarities in terms of the small-scale schemata and of the Schenkerian middleground plans. With regard to the larger context, this comparison shows both functional equivalence of different small-scale schemata as well as functional difference of identical schemata. In this context I suggest that tonal structure (and formal function) be understood in terms of schema networks consisting of short local patterns and overarching large-scale patterns.

Secondly, I will discuss a piano piece by Robert Schumann in which a strongly deformed reminiscence of the galant Monte schema helps to establish a coherent context that is very different from common tonal strategies. The analysis could be a starting point to discuss the function and aesthetic significance of 18^th century schemata in the ‘musical poetics’ of the 19^th century.

1. Galant Style: Mozart and Haydn

Wolfgang Amadeus Mozart, Allegro in B flat (K. 3)

Consider the young Mozart’s Allegro in B flat major. Gjerdingen’s analysis from Music in the Galant Style shows a simple juxtaposition of schemata (example 1). In contrast, in my synoptic analysis I show the schemata at different levels and with very different expansion (example 2).[4]

Example 1: Gjerdingen 2007, p. 340; Analysis of Wolfgang Amadeus Mozart, Allegro in B flat (K. 3) from the Music Book for Maria Anna Mozart (1762)

For example, successive schemata may overlap with respect to the different structural levels to which they belong. Just consider the beginning of the piece. At the moment when the Prinner in mm. 6f. is identified as such, the initial schema complex may be heard as a composing out of the Prinner’s first stage. The Prinner, for its part, modulates to the dominant and in this way contributes to articulating the penultima of the global cadence.

Example 2.1: Synopsis of a Schenkerian and a multi-scale schema analysis of Wolfgang Amadeus Mozart, Allegro in B flat (K. 3), mm. 1–12

The Schenkerian middleground plan of the piece is very typical for small binary forms in 18^th century. The 5^th degree is prolonged into the second section by a reaching over fifth progression, with the resolution of the dominant in a structural sense occurring only at the conclusion of the movement. From this point of view the thematic recapitulation in mm. 21–26 appears as a parenthesis, so that one may observe a tension between thematic design and tonal structure.[5]

Example 2.2: Synopsis of a Schenkerian and a multi-scale schema analysis of Wolfgang Amadeus Mozart, Allegro in B flat (K. 3), mm. 12/13–30

It seems to me undeniable that such “common tonal patterns”[6] or “large-scale tonal plans”[7], which ultimately may include what Schenkerians call the ‘fundamental structure’ or ‘Ursatz’, represent hierarchically super-ordinated schemata.[8] Although they are more general in respect of a piece’s detailed design than small-scale schemata in common sense, they aren’t necessarily less concrete in terms of their characteristic events and relationships, which are articulated (and made perceivable) by small-scale schemata. However, the question to what extent functional hierarchies in music are (at least in terms of pitch relations) ‘uniform’, i.e., based on the self-similarity of elements, patterns or structures in different scales and on different levels, is the subject of an ongoing debate.[9]

All three 18^th century pieces in question here follow variants of the same schematic middleground plan, which gives us a strong point of comparison. Furthermore, in all of them the reaching over progression of the second section is articulated by a Fonte schema.

Wolfgang Amadeus Mozart, Menuet in G (K. 1e)

Let’s now have a look at Mozart’s Menuet K. 1e (example 3). The comparison of the pieces will show that some schemata can be substituted for others with respect to certain functions they fulfill within the tonal context.

Example 3: Wolfgang Amadeus Mozart, Menuet in G (K. 1e)

While in Mozart’s Allegro it was the initial Mi-Re-Do schema that marked the primary note of the fundamental line and composed out the tonic, in the Menuet it is a neighbor note schema (➂-➃ / ➁-➂) that I named it my graph “Pastorella’s little sister” because it shares essential features with Gjerdingen’s Pastorella schema (➂-➁ / ➃-➂).[10] Furthermore, the linear progression, which ends with the tonicization of the dominant harmony in both pieces, is instantiated by different schemata. In place of the modulating Prinner there is a schema that one may call ‘galant Cadenza doppia’, because it starts with a Comma to a metrical weak tonic that initializes a complete cadence to a strong tonic (mm. 6ff.).

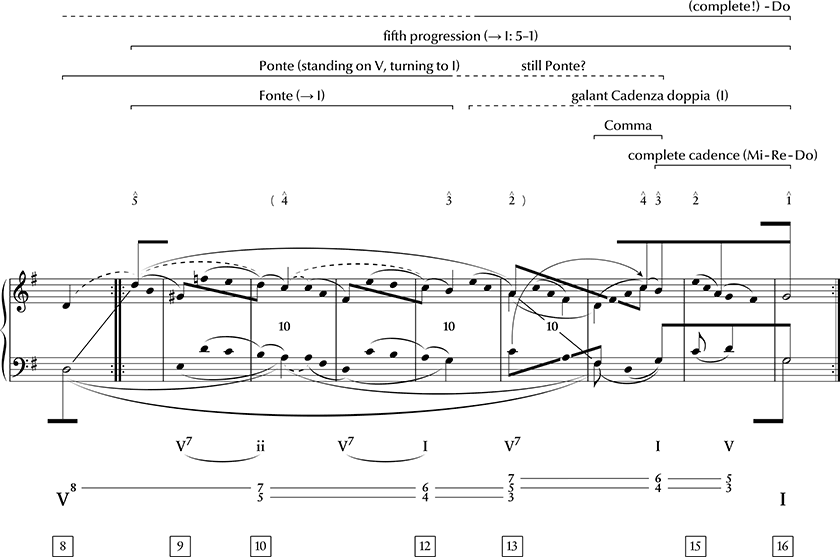
Example 4.1: Synopsis of a Schenkerian and a multi-scale schema analysis of Wolfgang Amadeus Mozart, Menuet in G (K. 1e), mm. 1–8

As in Mozart’s Allegro K. 3, after the double bar we see a Fonte schema (example 4.2). Although the same schema in the same formal position starts on the same degree, there is a significant increase in complexity. In the wider context, the Fonte’s upper voice proves to be a motion from the 5^th scale degree downwards into an inner voice, and only the unfolding back to the 4^th scale degree (m. 14f.) continues the reaching over fifth progression that completes the movement with a galant Cadenza doppia. Furthermore, the Fonte’s linear progression glosses over the imperfect tonic cadence (‘Grundabsatz’), while at the same time the unfolded 4^th scale degree in the upper voice is the starting signal of the final Cadenza doppia. Such overlappings and changes in function of events bring out aesthetic effects which may not be spectacular, but go beyond the intrinsic features or implications of the schemata that were used.

Example 4.2: Synopsis of a Schenkerian and a multi-scale schema analysis of Wolfgang Amadeus Mozart, Menuet in G (K. 1e), mm. 8/9–16

Joseph Haydn, Piano Sonata No. 27 in G, mvt. 3

Let us now consider the third movement of Haydn’s Piano Sonata No. 27 in G major. This piece is discussed also in Gjerdingen’s Music in the Galant Style.

Example 5: Gjerdingen 2007, p. 133; Analysis of Joseph Haydn, Sonata in G (Hob. XVI, no. 27), mvt. 3, Presto (1774–76)

Besides the Mi-Re-Do (➂-➁-➀) schema in K. 3 and the Pastorella-like schema (➂-➃ / ➁-➂) in K. 1e, the Meyer schema (➀-➆ / ➃-➂) that opens the variation theme of the Haydn sonata is a further opportunity to prolong (or bring out) the initial tonic with the third in the upper voice.

The continuation phrase (mm. 5ff.) again uses the Prinner for modulating to the dominant. But in contrast to the overall linear progression in Mozart’s Allegro K. 3, the Prinner seems incomplete, which—to quote Gjerdingen—means, that the composer recognized the possibility for an “alternate path”. (The local 4^th scale degree of the Prinner is reinterpreted as an unfolded middle voice while the third scale degree is omitted completely.) Interestingly enough, the option to leave the ‘path’ of the modulating Prinner already at its second stage (➅-➄) converges with a Schenkerian interpretation of its regular continuation (➄-➃-➂) as a subordinated progression into an inner voice.[11]

Example 6: Synopsis of a Schenkerian and a multi-scale schema analysis of Joseph Haydn, Sonata in G (Hob. XVI, no. 27), mvt. 3, Presto (1774–76), mm. 1–16

The phrase after the double bar works more or less like the one in Mozart’s Allegro, but with a clearly articulated interruption of the fundamental structure. Gjerdingen shows a juxtaposition of Fonte, Monte maggiore and half cadence. In contrast, the analysis of schema levels as well as the Schenkerian graph shows that both schemata—Fonte and Monte—operate at very different structural levels. The mere fact that the subdominant neighbor note C appears in the lower octave (m. 13) makes one hear the Monte (mm. 13ff.) as a subordinated motion into a middle voice, while the actual outer voices articulate what Gjerdingen calls (in other, less convoluted contexts) a Converging cadence.[12]

Example 7: Gjerdingen 2007, p. 160, “A simplified Converging cadence”

At least the Prinner fragment in the recapitulation phrase offers a motivic parallelism to the neighbor note motive of the Meyer schema and provides the basis for an unfolding to the primary note in its obligatory register (example 8, mm. 21f.). As in the modulating phrase before the double bar, the 4^th scale degree is presented as an unfolded middle voice note in the final cadence (➁-➀ is substituted by ➃-➆-➀).

Example 8: Synopsis of a Schenkerian and a multi-scale schema analysis of Joseph Haydn, Sonata in G (Hob. XVI, no. 27), mvt. 3, Presto (1774–76), mm. 17–24

A brief summary:

1. The mere identification of paratactically juxtaposed schemata says little about the function of schemata in a specific context. However, certain schemata imply typical formal and/or tonal contexts, and a typical context for its part may represent an overarching schema (or ‘plan’).

2. The supposition of ‘schema-levels’ assumes that a) schemata on separate levels are characterized by similar (i.e., primarily melodic, contrapuntal and harmonic) parameters and relations, b) that one and the same schema may be used at very different levels, and c) that Gjerdingen’s timid concept of a ‘diminution of schemata by schemata’[13] is transferable to a larger context. In this regard, a multi-scale schema analysis may engage with a Schenkerian analysis of structural levels.

3. Signal-like schema events imply a network of expectations that is continually being adjusted and differentiated in the course of further choices. However, these choices are governed by a network of interrelated large scale schemata. Slight variants in the schema configuration of the foreground may result in an exchange or realignment of schemata on deeper levels.

4. Compositional individuality may result from the variety of possible functional relationships between schemata on different structural levels. The way a schema is functionalized in a certain context may be uncommon or even singular, although the schemata used are themselves absolutely run-of-the-mill.

2. Musical Poetics: Robert Schumann, Album for the Youth, No. 21

In the light of the above, have a look at Schumann’s No. 21 of the Album for the youth. This piece exemplifies how conventions, in particular schemata and style figures of the galant style, can be revived in the idiom of early romantic compositions.

First, consider my recomposition with an (almost) regular succession of cadences (‘Kadenzordnung’) and a conventionalized Monte phrase after the double bar. Apart from the open, instable beginning and the surprising Cadenza sfuggita in m. 4, things are as they ought to be in a rounded binary.

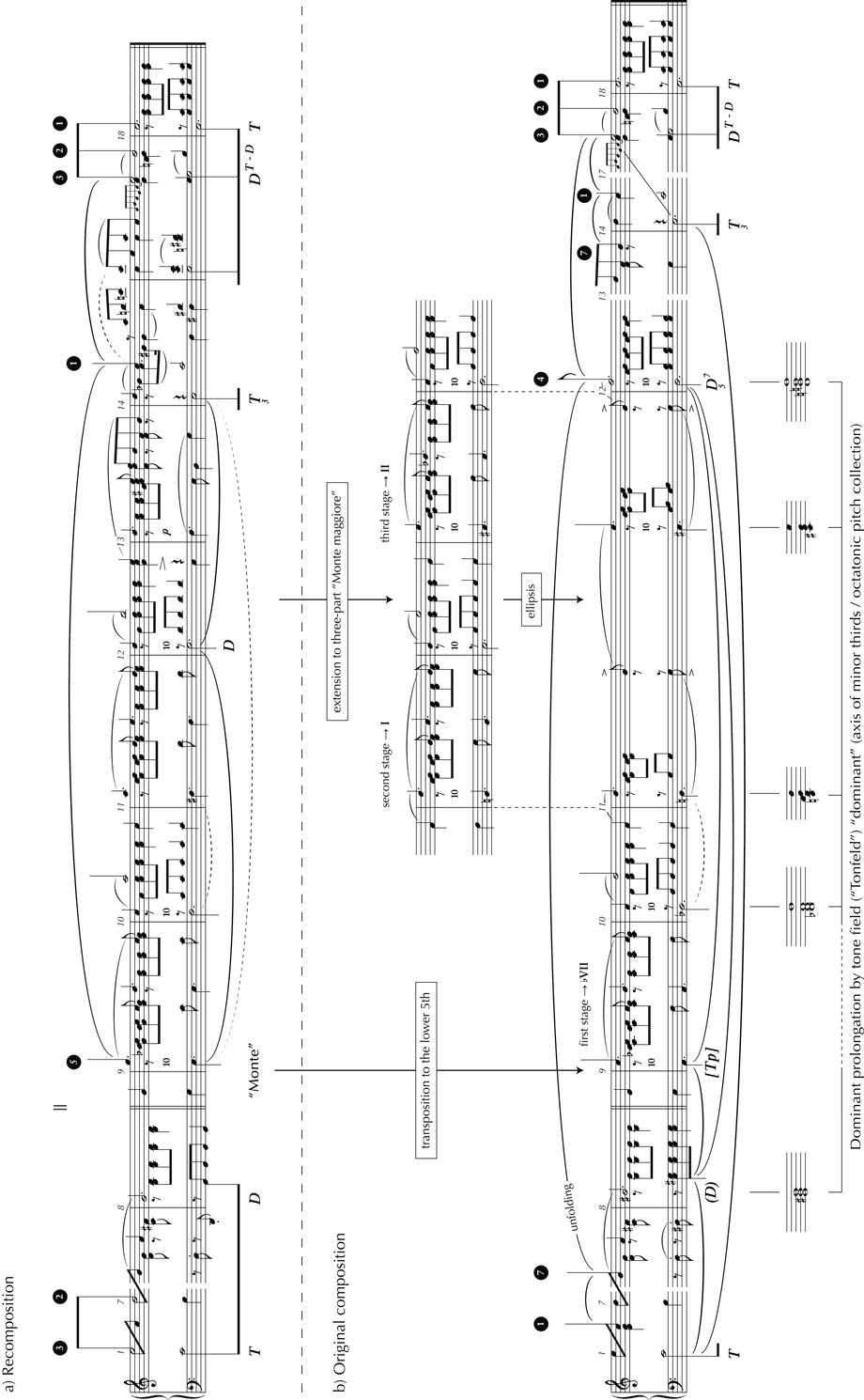
Example 9: Recomposition of Robert Schumann, Album für die Jugend, No. 21 (1848), with (almost) regular succession of cadences and a Monte phrase after the double bar

Now consult the analytical sketch in example 11 (further down). For sections of binary forms that begin with a Monte phrase, it is not untypical that the ‘point of interruption’ coincides with the formal division in m. 8 produced by the tonicization of the 5^th degree.[14] Tracing the voice leading after the double bar, one discover the line G-A-B-C, whose melodic goal, C in the second measure of the recapitulation (m. 14) marks the beginning of the final cadence. It appears one measure later in the register of the Monte’s upper voice and is then unfolded to the primary note E, which coincides with the cadential Mi-Re-Do schema.

Let’s now compare my conventional recomposition (example 9) with Schumann’s original composition (example 10). Three events stand out: the irregular deceptive cadence to E major before the double bar, a phrase that begins like a Monte schema with an irregular continuation, and the climax on the four-three chord of G major in m. 12.

Example 10: Robert Schumann, Album für die Jugend, No. 21 (1848)

The E major chord before the double bar may be understood as an applied dominant in A minor that is immediately chromatized to a dominant six-five chord in B flat major. This six-five chord and its resolution in this formal position acts as a strong schema event that suggests a rising sequence in the following measures.

As example 11 shows, one can engage in an intellectual exercise by reconstructing a series of operations (transposition, extension, ellipsis) through which Schumann’s composition can be regarded as the transformational result of the ideal-typical recomposition. Admittedly, it makes no sense to argue about whether the actual phrase after the double bar ‘is’ a Monte or not. However, in the act of communication, in the experience and the expectation of a ‘well socialized’ listener, the Monte idea is evoked by an aggregate of signals, which in this case depend in particular on aspects of shape and formal function.

Example 11: Analytical sketches about Robert Schumann, Album für die Jugend, No. 21 (1848); a) recomposition (compare ex. 9), b) original (compare ex. 10)

The question arises as to why the piece, and particularly the deformed Monte phrase, may be perceived not only as surprising, but also as very clear, coherent and focused. From a Schenkerian perspective one may hear the upper voice of the pseudo Monte as a linear progression that leads from B to F (mm. 7/8–12). It thereby articulates a tritone unfolding to the seventh of the dominant seventh chord. The presentation of F as the upper neighbor note of the belated primary note E seems to be a key event of the tonal process.

Admittedly, the function of the E major chord for the entire piece remains more or less enigmatic from a Schenkerian point of view. In my perception, it creates a very special aural effect. The three closely spaced chords E major, B flat major and G major7 appear to me as different illuminations or colors of a single Klang rather than different harmonic degrees in the usual sense. This effect may also be due to the fact that these chords lie on an axis of minor thirds and include the notes of an octatonic pitch collection. In the aural effect of this dominant ‘Tonfeld’ (tone field), the difference between the ‘parallel’ chords E major, B flat major and G major7 is essentially levelled. In this sense one may hear a ‘dominant prolongation’ in the middle of a piece, but transferred to a historically later mode of tonality (see below example 11b).[15]

Schumann plays a game of make-believe. Numerous signals suggest a piece that is still bound to traditional tonal and formal schemata which are partially distorted. But what seems to be a distortion (or alienation) observes new rules. Indeed, certain effects in musical poetics of the 19^th century seem due to the fact that the ‘Ursatz-tonality’ and its common patterns and procedures are no longer self-evident, allowing for the reemergence of other modes of musical coherence.

The Monte idea acquires an atypical realization in a historically late mode of tonality. It would be an unacceptable reduction to equate the schema with its ideal-typical formulation (not only in this case). On the other hand, the schema remains recognizable since similarity in shape and functional determination are interlocked: because of the moments that can be related to the shape of the ideal type, expectations are raised and functional attributions evoked. These act as signals that guide our perception of even those sections that are only partially similar to the ideal type.

To understand what happens when small-scale schemata are used in new ways, that is, in contexts that are not ruled by those tonal Metaschemata (or plans) by which they originally (that is in galant style) were functionalized, let me cite an aphorism of Novalis from the Fragments on poetry (1798): “Die Kunst, auf eine angenehme Art zu befremden, einen Gegenstand fremd zu machen und doch bekannt und anziehend, das ist die romantische Poetik.” (“The art of disconcerting in a pleasant manner, of rendering an object alien and yet familiar and appealing, that is romantic poetics.”)[16]

Conclusion

In terms of schema theory, Schenker’s motto—“always the same, but not always in the same way”[17]—may be used bottom up instead of top down: Although the small scale schemata of traditional music are always the same, the functional relationships they assume within one entire piece may be unique. On the other hand, in some 19^th century music it is precisely an individualizing and atypical instantiation of older schemata that creates new effects and contributes to new tonal strategies.

Most tonal compositions have aesthetic features and effects which go far beyond the intrinsic features of the schemata used. If schema theory lays claim to be a theory of art in an emphatic sense, it will have to consider the function of schemata in the context of entire pieces. For this reason, a central task of further research will be—in my opinion—to examine the extent to which the schema concept itself allows emphasizing functional hierarchies or at least connecting with theories that do so.