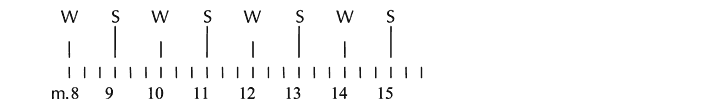Breaking the Frame: Arabesque and Metric Complexity in the Sunrise Scene from Ravel’s Daphnis et Chloé (1912)[1]

Polyrhythm in Ravel is nothing more than the scrupulous fidelity to nature, the versatility of an expression which varies with the slightest emotional change…this detailed and juxtalinear realism…helps to stop any habits from setting in; it forces us continually to readjust ourselves and breaks any rhythmic constellations which might have become encrusted; it prevents the music from drifting into the conventional purring of one rhythm selected once and for all, in fact it keeps us supple by the exercise it imposes on us, it keeps the mind turned towards truth and life.[2]

I could not begin to explore Maurice Ravel’s conception of rhythm and meter without taking a moment to recall Vladimir Jankélévitch’s insightful remarks from his monograph on Ravel. In a section called “Rhythms,” Jankélévitch distills the most idiosyncratic features of Ravel’s compositional aesthetic into these few, evocative phrases. Although subsequent scholars have struggled to conceptualize the sense of fluidity, ambiguity, and irregularity inherent to Ravel’s rhythmic/metric language, Jankélévitch’s intuitions seem to have led him in a fruitful direction. He acknowledges a range of techniques that characterize Ravel’s metric style including frequent changes of time signature, asymmetric meters, syncopation, and weak metric articulation. At the same time, Jankélévitch confers a special status to Ravel’s alignment of polyrhythm—by which I assume he means superimposed/juxtaposed distinct rhythmic patterns—with musical expression. Jankélévitch views the resulting “polyrhythm of expression” as being a constitutive aspect of Ravel’s technique, and subsequently invests the contrapuntal complexity of such layers with narrative meaning.[3] In Noctuelles, polyrhythm connotes the “frenzied zig-zag flights of the big moths;” in Petit Poucet, it reflects “the wanderings of the children lost in the forest.”[4] His sensitive analyses open our ears to Ravel’s high regard for the expressive potential of rhythm and meter, while suggesting ways in which we might allow these parameters to assume a more active and evocative role within the musical process.

This philosopher’s musings are of particular significance at the present time for it is only in the last thirty years or so that music theorists have begun to re-examine rhythm and meter with a renewed sense of rigor and creativity. A range of scholarly voices has shaped this discourse through the proposal of theories and methodologies that have brought the most basic tenets of metric theory into question. These include the definition, conceptualization, and cognition of meter, as well as a consideration of how meter might participate to create expressive meaning within distinct musical contexts. While observing these lively debates along with their diverse theoretical claims, my attention in this paper will be limited to a select range of ideas that inform an exploration of Ravel’s techniques in particular, and debut-de-siècle French repertoire in general.[5]

Following Jankélévitch’s cue, I will engage primarily with the work of Harald Krebs and Richard Cohn, both of whom focus on the structural and expressive implications of congruent and non-congruent interaction between rhythmic layers. Krebs’s conceptualization of metrical dissonance is especially useful for capturing distinguishing traits of Ravel’s contrapuntal writing.[6] While his definitions permit considerable descriptive precision, they acquire even greater clarity when combined with Cohn’s notions of double and complex hemiola as visualized on his ski-hill graphs.[7] This is especially the case in contexts that explore simultaneous, multi-level dissonances. Other scholars whose work has helped me to articulate Ravel’s metric peculiarities include Jonathan Kramer, Gretchen Horlacher, and Justin London. Kramer’s thoughts on hypermeter and metric reinterpretation illuminate Ravel’s construction of “fragile” metric hierarchies.[8] Horlacher’s privileging of metric irregularity as characteristic of an evolving, dynamic process in Bartók offers several points of intersection with Ravel’s manipulation of metric fluidity.[9] Justin London’s latest cognitive evidence reinforces my claim that Ravel challenged his listeners by operating within an exceptionally wide metric hierarchy; one that gave prominence to lower levels, whose noticeable presence is especially important to this study.[10]

My paper will examine an episode that displays Ravel’s metric wizardry at its most refined, the Lever du jour (Sunrise Scene) from his 1912 ballet, Daphnis et Chloé. At the centre of our musical experience is a melodic figure that I shall call the arabesque motif. This label suggests how short rhythmic values are organized to trace the “S-curve” of contemporaneous visual arabesque through a periodic descending and ascending melodic contour.[11] The undulating motif’s initial characterization as an inconsequential decoration betrays its growing significance as a metric, formal, and narrative catalyst. Although this triplet 32^nd motif outlines a formal frame for this scene, we will see how its constant presence, yet fluctuating prominence, brings into central view shifting irregularities and conflicts on and between other levels of the metric hierarchy. By incessantly coming in and out of auditory focus, we never know whether this motif is a background accompaniment or something more substantial until the dramatic juncture of Daphnis’s awakening. At this moment, the motif bursts into the foreground to suggest the symbolic fusion of nature, divinity, and human emotion. The structural role of the arabesque motif on metric and narrative levels unsettles prevailing viewpoints of ornament as meaningless and non-essential. In so doing, this figure indicates Ravel’s vibrant conception of the metric hierarchy and its inter-relationships, while promoting a vital convergence of meter, musical form, and drama.

* * *

The libretto for Daphnis was created by Michel Fokine and is based on the ancient Greek pastoral romance by Longus. In Part One, we see the meeting of the main protagonists, Daphnis and Chloé, and witness how Daphnis woos Chloé in a dance competition. After obtaining his prize, Chloé’s kiss, Daphnis falls asleep, and suddenly awakens to the cries of invading pirates who abduct Chloé. Part Two opens in the Pirates’s camp where Chloé is forced to dance for them. Unexpectedly, Pan appears and is able to save Chloé in the ensuing chaos. The depiction of sunrise signals the climax of the narrative and opens Part Three of the ballet. Daybreak has an important dramatic function in Ravel’s setting: it signals a new beginning as facilitated by Pan, and marked by the reunion of Daphnis with Chloé.

My interest to examine this over any other episode of the ballet is due to the unusual overlaps that emerge between the different temporal frames of this scene. On one level, we have the rhythm of the drama, with Part Three corresponding to the moment of plot resolution. This is heard against the natural rhythm of the rising dawn, which is itself depicted by a variety of specific rhythmic and metric techniques in the music. Each of these “rhythms” proceeds in its own time, and it is a lack of synchronicity that lends this episode its ambiguous and fragile status as the ballet’s apotheosis.

As Ravel indicates in his score, it is nature’s rhythm that we are first aware of as symbolized by the murmuring arabesque motif: “Aucun bruit que le murmure des ruisselets amassés par la rosée qui coule des roches.” This association is extended to the sleeping Daphnis, who is seen lying in front of the Nymphs’s grotto: “Daphnis est toujours étendu devant la grotte des Nymphs.” Sitting on the lower level of this scene’s metric hierarchy, the 32^nd motif finds more support on higher rather than intermediate pulse levels; from the opening measures in 4/4 we hear whole-note, quarter, and triplet-eighth pulses rather than 16^ths. Even following the sudden metric contraction to 3/4 in measure 5, it is only as more of the stage is gradually revealed that other levels of the metric hierarchy are activated.[12] When dawn finally begins to break at measure 8 (“Peu à peu le jour se lève”), we hear a wider range of pulses including 32^nd, duple eighth, triplet eighth, quarter, and dotted half note. The correspondence between a gradual activation of the metric hierarchy and animation of the drama is significant: the 32^nd motif, prominent in the first few measures, gently recedes to become a background figure at sunrise. From this point onwards, the repetitive arabesque motif comes to stand in for nature’s murmuring streams, although its unruly tendency to constantly push towards the foreground also suggests a more turbulent force, one that we might associate with Daphnis’s troubled subconscious.

As many a commentator has noticed with regard to Ravel, he seems to thrive on manipulating his listener’s expectations of musical continuity. This is especially apparent in his treatment of the arabesque motif. When stage events are minimal, such as at the opening and closing of the scene, this figure is at the forefront of our auditory perception. Even as it occupies our attention, however, the motif is restricted to a musical “frame,” and therefore assumes an overarching subsidiary function. This subordinate role is reinforced by the fact that the motif is static in terms of its rhythmic and metric development, and subject only to mild motivic modifications. As we may deduce from Ravel’s exposure of this motif in high woodwind registers at the opening, shifting timbres are perhaps the only factors to control the intensity of its appearance within the musical texture. Because this motif remains largely unchanged, it suggests a relatively marginal participation in the advancement of the plot—which initiates forward momentum towards narrative resolution—or of the scene—which requires the progressive articulation of natural time. Its status is revised, however, when we analyze this episode in relation to the music’s suggestion of a bar-form structure; in this context, the mesmerizing motif begins to disclose its underlying agency. In now examining the rhythmic complexities embedded within this motif, we shall consider how it facilitates other rhythmic and metric conflicts that conspire to prepare the dramatic and musical climax of the scene: the lovers’ reunion.

* * *

Table 1. Bar form in the Sunrise Scene

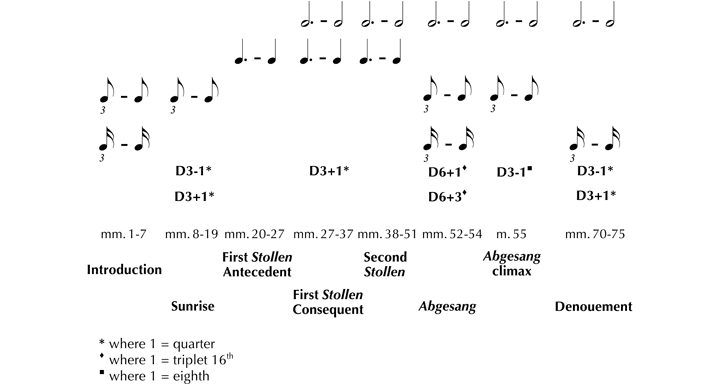
Table 1 outlines the formal structure of this scene. We should note that the sunrise music of mm. 8–19 is also heard at the end (mm. 62–75) to form a musical frame. This frame surrounds three large melodic phrases, which suggest the most basic type of bar-form construction: AAB. Each repeated Stollen (A) comprises two phrases joined in an antecedent-consequent pair. The Abgesang (B), though relatively short, also consists of a contrasting pair of phrases: the first half based on the theme associated with Chloé and first heard at Rehearsal 29⁺⁴; the second based on the theme associated with Daphnis and first heard at Rehearsal 1⁺⁶.

Given that the arabesque motif is heard throughout this scene, one would assume that it functions as an ostinato. While it certainly fulfils this role it does so in a particularly deceptive way, since unlike most ostinati this one is by no means a stable background event (as I have already hinted). Upon considering the motif’s rhythmic profile, we might initially be tempted to dismiss its significance, citing the twelve tripleted 32^nd values as falling beyond our auditory range of perception, and therefore unworthy of the hard work we would have to invest as listeners attending to this level. (See Example 1)

Example 1. Arabesque motif, m. 1

Justin London characterizes this tendency in his simulated listener response to Variation 5 from Bach’s Goldberg Variations, which has a similarly constructed endless stream of short rhythmic values, in this case, 16^ths: “the listener [might] not know if the rapid activity will continue and thus reward his or her continued attention at the smallest/most rapid levels of motion.”[13] At the same time that London describes such figurations as being “metrically overdetermined,” he also claims that the ongoing presence of short rhythmic values might encourage the listener to change his/her expectations of this pulse level.[14] In proposing a range of “upper and lower bounds [that] can be regarded as a kind of temporal envelope for meter,” London offers evidence to support our careful attention to the arabesque motif.[15] He claims that “the lower limit for meter, that is, the shortest interval that we can hear or perform as an element of rhythmic figure, is about 100 milliseconds (ms).”[16] Looking at the arabesque motif against the metronome marking for this scene (Lent, quarter=50), it appears to fall exactly within this range (100 ms). Even though this temporal level might not be the obvious one that we entrain to, London’s evidence suggests that we may entrain to groupings of the triplet 32^nds rather than their individual attacks within a metric layer. Keeping in mind the several grouping possibilities that are present let us now study the motif’s rhythmic ambiguities with a view to understanding its larger role within the metric and formal process.

Example 2. Dissonance in the arabesque motif, m. 1

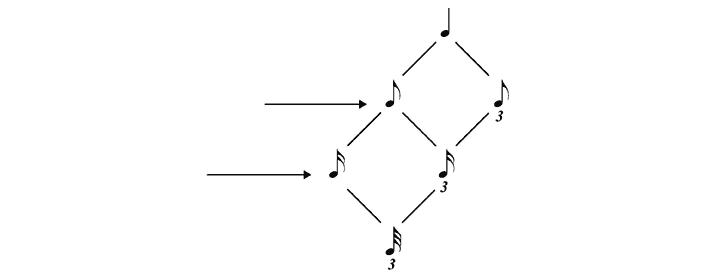
Example 2 shows how the E⁵, D⁵, and C⁵ descent within the motif suggests a triplet-16^th pulse, which yields a 200 ms layer that lies at the lower threshold of our metric perception. However, an attack on A⁴ on the 4^th, 7^th, and 10^th 32^nd pulses accentuates a duple-16^th pulse, which yields a 300 ms layer that lies more comfortably within the range of our metric perception. The ensuing conflict between triplet and duple-16^th pulses is also mirrored on an eighth level: the triplet eighths of the bass melody conflict with the implied duple eighths of the duple-16^th subdivision. Furthermore, both dissonances are embedded within the periodic quarter pulse that is sustained by the motif through accents of register and re-initiation.

Example 3. Double Hemiola as shown on Richard Cohn’s ski-hill graph

Example 3 captures the metric complexities of this motif on Richard Cohn’s ski-hill graph. This diagram indicates the various pathways that might govern our perception of the motif. Moving downwards on the graph from the quarter pulse we find two possible divisions: the rightward path divides the quarter pulse by three to the triplet eighth; the leftward path divides it by two to the duple eighth. The triple division corresponds with a 4+4+4 grouping of the motif; the duple division corresponds with a 6+6 grouping. Similarly, moving downwards from the duple eighth pulse there are two possible divisions: the rightward path extends to the triplet 16^th while the leftward path extends to the duple 16^th. The triple division explicates the E⁵-D⁵-C⁵ descent to give the following grouping: 6=2+2+2. The duple division follows the prolongation of the pitch A⁴ to give the following grouping: 6=3+3. We thus hear a hemiola at two levels (a “double hemiola”) as shown by arrows in this example. The graph shows an additional inner zig-zag pathway, which Cohn calls “slalom” in keeping with his ski analogy.[17] This combines duple and triple values (quarter, duple eighth, triplet 16^th), and suggests further complexity in the simultaneous perception of the motif as triple on one level and duple on an adjacent level.[18]

The arabesque motif is undoubtedly ambiguous and it is difficult to conceive of any one pathway as representing the primary metric consonance of this scene. While we might choose to focus on those pulse levels that fall into our innate preferred range of listening, Ravel’s treatment of this motif is exceptionally demanding and pulls the listener in more than one direction. For example, following the rhythmic ambiguities of the arabesque motif in the introduction (mm. 1–7), the quarter and duple-eighth pulses of the sunrise melody resonate with our hearing of similar pulses in the motif. By activating intermediate levels most likely to be felt as the tactus, Ravel thus establishes a stable, if somewhat delayed, articulation of the notated 3/4 meter in m. 8. However, this stability is short-lived since the immediate emergence of ‘bird song’ (in the form of triplet eighths, triplet and duplet 16^ths, and triplet 32^nds) seems to simultaneously direct our attention towards lower metric levels. Coupled with two displacement dissonances that begin at the apex/descent of the sunrise theme in m. 15 (D3-1 where 1=quarter in the basses, cellos, tubas, horns, and bassoons; and D3+1 where 1=quarter in the winds and violins, Example 4), this entire section seems to encapsulate a distinctive feature of Ravel’s metric style: the unstable articulation of metric stability, also perceived as the immediate destabilization of a shortly achieved stability.

Example 4. Displacement dissonances at the sunrise melody denouement, m. 15

The portrayal of sunrise is a key dramatic event that has taken place by the end of the introduction, and it is important to note Ravel’s subtle association of natural rhythm with metric instability (a link that I explore later in the paper). Even though he immediately retracts from the displacement dissonances established by the end of the introduction, the two Stollen that we will now examine pursue increasing levels of instability as the narrative moves towards acknowledging another natural phenomenon, this time tinged with a divine aura: Pan’s rescue of Chloé.[19]

Turning then to the first Stollen, we hear how the arabesque motif moves into the background while two melodic phrases play against the established meter through a number of grouping dissonances. We first hear direct dissonance (G3/2 where 1=eighth) between a quarter and dotted-quarter-pulse in m. 21, which appears to prepare a slightly longer occurrence of the same in mm. 23–25.[20] This allusion to 6/8 is suspended by the momentary intrusion of a distant shepherd in m. 26. The 64^th values of his non-metric flute melody seem to stretch the measure to 4/4, and thus emphasize the short values of the arabesque motif within the texture (incidentally, this is already fairly prominent at this moment given the absence of melodic material emanating from the Stollen). The shepherd does not seem to have been distracting enough, since the second phrase of this Stollen initiates grouping dissonances on additional metric levels in conjunction with displacement dissonance. As well as the quarter/dotted-quarter dissonance that we hear at the close of this phrase (m. 35), we also hear a G6/4 (where 1=eighth) between half-note and dotted-half-note pulses from mm. 29–30, followed by displaced downbeat emphasis in m. 32 and m. 34 as we witness another passing shepherd (D3+1 where 1=quarter).

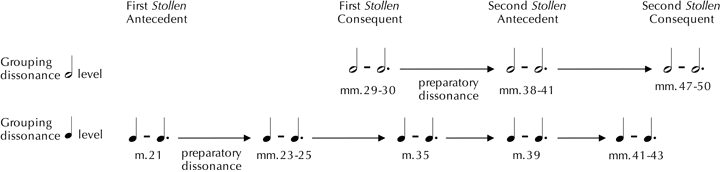
Figure 1. Dissonance preparation in the Stollen, mm. 21–50

Krebs’s notion of dissonance preparation is crucial to understanding the way in which Ravel develops the phrases of each Stollen (Figure 1). In the second Stollen, for instance, a repetition of the first phrase, including the quarter/dotted-quarter conflict, is now accompanied by the half-note/dotted-half-note dissonance of the second phrase (mm. 29–30) for a considerable duration in the wordless chorus (mm. 38–41). The same grouping dissonance occurs at the corresponding moment of the second phrase and is sustained for a longer period (mm. 47–50).

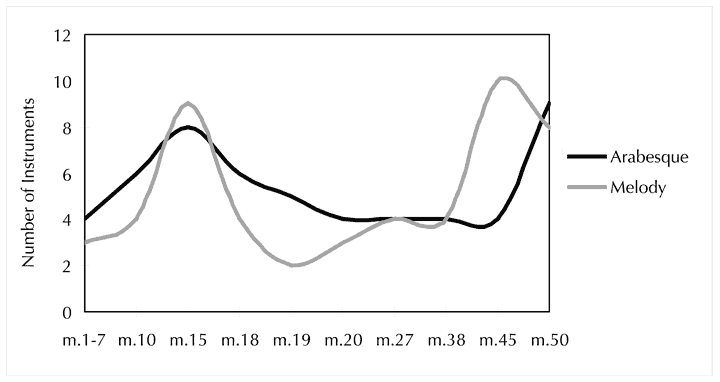
It is significant that the increasing intensity of grouping dissonance in the Stollen is accompanied by another progression: the rising textural prominence of the arabesque motif. While the 32^nd motif has been balanced by melodic material in the Stollen, its dominant emergence at m. 49 seems to have been anticipated at several moments: it is left suspended in the texture at m. 19 (before the start of the first Stollen), and pushes forward again at the entrances of the shepherds in m. 26 and m. 31, as well as the corresponding moment in the second Stollen, first phrase, m. 44. By the end of the second Stollen, the arabesque motif has saturated the entire woodwind section in preparation for the important textural inversion that is about to take place at the Abgesang. I have attempted to capture the shifting balance of the arabesque motif in Figure 2. This graph represents an approximate measure of amplitude—not a precise one—that takes into account instrument doublings.

Figure 2. A graph showing the shifting balance between the arabesque motif and melody, mm. 1–50

The surfacing of the arabesque motif is dramatically linked to a third appearance of shepherds who first look for Daphnis (“Entre un groupe de pâtres a la recherche de Daphnis et Chloé,” mm. 46–47), and then awaken him upon finding him (“Ils découvrent Daphnis et le réveillent,” mm. 50–51). It is the moment of Daphnis’s awakening that marks the beginning of the Abgesang and the arabesque motif’s conspicuous presence. While the motif’s previous intermingling with the shepherds’ flute melodies was purely evocative in its depiction of the scene, this occurrence is fraught with narrative tension as captured by Ravel’s commentary on Daphnis’s state of mind: “Angoissé, il cherche Chloé du regard,” (m. 52). Tellingly, it is the metric language that portrays Daphnis’s mental anguish as he frantically searches for Chloé.

Several factors highlight the connection between Daphnis’s anxiety and the arabesque motif in this section. First is the presentation of the primary melody in triplet 16^ths, which necessarily diverts our attention to short rhythmic values in the texture. This emphasis on the lowest metric level is dramatized through a significant rhythmic transformation of Chloé’s melody from Rehearsal 29⁺⁴ (Example 5). The transformation of each quarter of Chloé’s melody into a triplet 16^th in m. 52 facilitates several displacement dissonances that saturate the Abgesang. For example, the displaced downbeat stress of Chloé’s 3/4 melody is retained in the new viola melody as D6+1 (where 1=triplet 16^th) as opposed to the original, D6+1 (where 1=quarter). The displaced agogic and density accents of her original melody (D6+3 where 1=quarter) are also manifest in their transformation into displaced eighth pulses, D6+3 (where 1=triplet 16^th).

Example 5. A comparison of Chloé’s melody at Rehearsal 29 with its transformation in m. 52

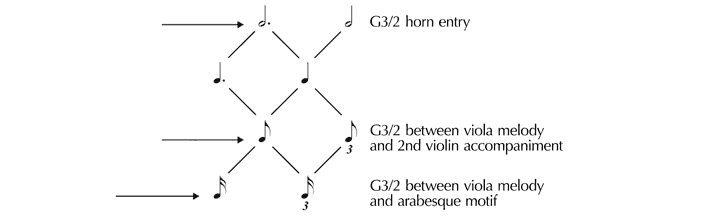
These displacements form an unstable background against which several additional grouping dissonances are projected. The combination of displacement and grouping dissonances here demonstrates Yonatan Malin’s concept of a “displaced hemiola.”[21] Because distinct dissonances are often heard simultaneously they also correspond to what Richard Cohn defines as a complex hemiola.[22] I show these relationships in the ski-hill graph of Example 6. The first of these conflicts is a G3/2 between the triplet-16^th pulse and the subliminal duple-16^th pulse that pervades this scene as implied by the arabesque motif. A second is the displaced hemiola, which combines a G3/2 between an implied duple-eighth pulse (projected by the triplet-16^th viola melody), and the triplet-eighth pulse of the displaced second violin accompaniment (D6+1 where 1=triplet 16^th); the duple-eighth pulse is sustained through the tremolo triplet 16^ths of m. 54, and thus suggests an indirect dissonance against the preceding displaced triplet-eighth pulse of the violin accompaniment (G3/2). We hear an additional G3/2 on a higher metric level between the half-note pulse of the horn entry (mm. 53–54), and the notated dotted-half-note pulse. This specific dissonance pays tribute to Chloé’s theme, which prolonged a similar dissonance for twelve measures between Rehearsal 29–31 in conjunction with a displaced half-note pulse (D2+1 where 1=quarter). Finally, the fragmentation of Chloé’s theme into tremolando 16^ths as it ascends several registers transforms Daphnis’s anxiety into elation as he witnesses her appearance: “Elle apparaît enfin, entourée de bergères.”

Example 6. A complex hemiola captured on Cohn’s ski-hill graph, mm. 52–54

Just as Chloé falls into Daphnis’s arms (“Ils se jettent dans les bras l’un de l’autre”), her melody leads seamlessly into a return of Daphnis’s theme to mark the narrative and formal climax of the Abgesang (m. 55). As with Chloé’s theme, Daphnis’s melody is also subject to rhythmic modifications, which are a consequence of his melody’s new metric placement in 9/8. The influx of 32^nds—as tremolando 16^ths—into the textural foreground at m. 54, and their concomitant unison possession of the melody, has an overwhelming effect on the notated meter: this now seems to expand from 3/4 to 9/8 in m. 55 as Ravel attempts to make the moment of their reunion last even longer. One significant consequence of this metric expansion is the eventual normalization of the triplet eighth pulse, which has been vying for attention since the opening measures. As a result, the arabesque motif, which had previously assumed an ambiguous metric identity, now emerges in a 4+4+4 pattern that marks the triplet eighth pulse as a primary metrical layer.

Like Chloé’s melody, the rhythmic and metric transformation of Daphnis’s theme is not without several instances of instability. Similar to Chloé’s transformed theme is the emphasis on displacement dissonance characterized here through syncopation: the second dotted-quarter pulse in m. 55 and m. 56 is an eighth too early (D3-1 where 1=eighth). Also related is the indirect dissonance (G3/2) created by the triplet eighths of Daphnis’s melody, which conflict with the previous eighth pulse of 3/4. This technique carries over into mm. 57–58 where the melodic grouping now articulates a half-note pulse that conflicts with the dotted-half-note pulse initiated by the return to 3/4. Unlike Chloé’s theme, however, we do not hear Daphnis’s melody from Rehearsal 1⁺⁶ in its entirety; Ravel chooses to focus only on the first two measures before he transforms the remainder of the phrase (mm. 57–59) to resemble the falling fourth-fifth interval from the denouement of the sunrise phrase (mm. 15–19).

This subtle melodic transformation has larger narrative and musical implications given that it offers a fleeting glance of the latent link between Daphnis, his reunion with Chloé, and natural power as personified by Pan.[23] Ravel emphasizes this trinity early on in the ballet; the first time we see Daphnis and Chloé (Rehearsal 16, “Emotion douce à la vue du couple”) they appear against the backdrop of a solo flute arabesque melody that opens the ballet and is emblematic of Pan ever since.[24] This nexus of associations is brought into focus again at mm. 60–61, the only time, other than the opening of this scene, where the arabesque motif is exposed. Here, it is supported by the angular melodic motif that announced Pan’s arrival at the moment of rescue (Rehearsal 147). Textural emphasis on the arabesque motif accentuates a central narrative turning point: Daphnis’s awareness of Pan’s divine intervention as signified by Chloé’s crown (“Daphnis apercoit la couronne de Chloé. Son rêve était une vision prophétique: L’intervention de Pân est manifeste.”) With the immediate return of the opening sunrise music at m. 62 the entire realm of nature appears to celebrate Pan. Unlike the portrayal of daybreak, however, what is interesting at this moment is the intensity of dissonance that marks this tribute beginning at the denouement.

As in the second Stollen, the addition of wordless voices from Rehearsal 168 introduces a G3/2 between the notated dotted-half-note pulse and their own half-note pulse. This is superimposed above two displacement dissonances as heard in the opening sunrise: D3-1 where 1=quarter (lower strings and brass), and D3+1 where 1=quarter (violas, violins, Cor Anglais, oboes, and flute). These dissonances form a displaced hemiola with the G3/2 between the triplet-16^th pulse of the Glockenspiel and implied duple-16^th pulse of the arabesque motif in 3/4. Grouping and displacement dissonances are prolonged until m. 76 where a triplet-eighth pulse creates indirect dissonance against the preceding eighth pulse in preparation for another move towards 9/8, this time associated with the lovers’ pantomime of Pan and Syrinx in homage to Pan.

* * *

Our overall experience of meter traces a gradual intensification of dissonance that peaks at the Abgesang and remains prolonged through the end of the scene as we approach the final celebration of Pan.

Figure 3. Increasing levels of dissonance accumulate at the Abgesang, mm. 1–75

Figure 3 outlines this metric trajectory by detailing the types of dissonances associated with the introduction and frame, and their infiltration of central phrases. Even as we infer a migration of dissonance from the frame to the Abgesang and final denouement, we should also consider Ravel’s hypermetric organization of the scene, which suggests an unusual parallel on higher metric levels. Unlike my earlier plea to consider the metric participation of lower levels, my interest to examine higher level metric activity is more speculative given that theorists remain divided on whether listeners can really attend to what Jonathan Kramer calls, “deep-level meter.”[25] My observations are thus restricted to a discussion of pulses no higher than the level of the measure, which are grouped further into larger units. I once again find support in London’s view and investigation of hypermeter as an extension of the metric hierarchy in the opposite direction to the levels we have been examining until now: “Having several levels of metric structure present above the perceived beat is no more extraordinary than having several levels of subdivision below it.”[26] In keeping with such theorists as Kramer and Horlacher who are willing to entertain the possibility of higher metric levels—particularly levels that do not necessarily have to be present at all times or in regular patterns to assume legitimacy—we will see that Ravel’s conception of meter as fluid and dynamic is just as dependent on oscillations between stability and instability at higher levels as it is on lower levels.[27] Moreover, Ravel’s careful attention to shifting hypermetric patterns suggests his interest to extend the expressive potential of meter beyond the confines of the measure.

Table 2. Summary of hypermetric units

Looking at Table 2, we notice that the scene opens with a 4-measure unit, the only time that we hear a regular phrase before the Abgesang. The transition to irregular phrase groupings coincides with the metric contraction to 3/4 at m. 5, the notated meter for the remainder of this scene. On the whole, this Table reflects Ravel’s privileging of irregular hypermetric units. Prime proportions of phrases up until the Abgesang indicate that hypermetric spans are most irregular during the opening and central pair of Stollen, only to become regular towards the end of the scene. Unlike the rising intensification of dissonance that we have seen on lower metric levels, the transition from irregular to regular hypermetric organization is an immediate occurrence rather than a gradual development. This observation becomes transparent once we place the two pillars of this scene’s musical frame side by side. Even as the opening and closing portions share a considerable number of rhythmic and melodic features—facilitated primarily through the repetition of the sunrise melody—their hypermetric units are entirely opposed: the introductory sunrise fluctuates between a shifting succession of irregular metric units, while the closing section is regular.

Example 7a. Regular alternation between strong (S) and weak accents is interrupted by the consecutive placement of strong accents

Example 7b. Metric re-interpretation of mm. 8–15

This contrast may be attributed to Ravel’s altered treatment of the sunrise material in the closing portion of this scene. Although we hear two-measure units in the first presentation of this phrase (m. 8), the structural emphasis of this passage—conveyed by accent of change and register at the melody’s apex/descent in the tonic—occurs one measure too early (m. 15). Example 7a shows that we hear this premature accent on the anticipated second beat of a two-bar hypermeasure rather than the downbeat of m. 16.[28] Depending on how high up the metric hierarchy we are prepared to listen, the weak placement of this accent might have repercussions for the four-measure unit (where it occurs on the weak fourth measure) and the—even higher—eight-measure unit (where it marks the weak eighth measure). Following cognitive evidence provided by Candace Brower, it is possible that the ‘misplacement’ of the accent shifts our perception of the entire phrase to motivate, in retrospect, a reinterpretation of the melodic entry at m. 8 as weak in order to interpret the accent as strong (Example 7b).[29]

In contrast to the irregular hypermetric patterns of the opening, Ravel creates regular units when he repeats the sunrise melody towards the end of this scene (mm. 62–75). At this point, the melodic ascent of mm. 62–69 is heard within an eight-bar span, which allows the upcoming structural accent to fall on the downbeat of a successive eight-measure phrase (mm. 70–77). The move towards regularity at this point might not seem so unusual given that we have progressed towards the end of this narrative episode; in Ravel’s effort to create closure such an arrival might be perceived as even more stabilizing given the irregularity of preceding hypermetric units. What is unexpected, however, is that the regular units of the final frame have been prepared not just in passing, but at the most dissonant formal juncture of the scene: the Abgesang.

It is particularly puzzling that the intense metric conflicts of the Abgesang mark the moment at which Ravel switches to a regular hypermeter. While the motivation to install hypermetric regularity at this point seems to respond to an expressive stimulus—one that takes into account the narrative resolution of this scene—it also reveals an intrinsic feature of Ravel’s metric style: the subsuming of lower level dissonances by higher-level metric stability. This observation also extends to the organization of the Abgesang at the level of the measure since it is an irregular 3+5 subdivision that constitutes the eight-measure unit: Daphnis’s conscious anxiety (2 measures) and Chloé’s emergence (1 measure) form a three-measure unit, while their embrace is sustained through 5 measures.

Ravel’s construction of a “stable-instability” is thus reflected in the move towards regularity on higher metric levels as accompanied by excessive instability on lower metric levels. As I have shown elsewhere, this fragile formulation need not always be nestled in this way; Ravel often creates metric structures where lower-level stability supports higher-level irregularity.[30] What we should extract from this observation is Ravel’s tendency to form deep hierarchies that are riddled with contradiction: stable relationships between some levels, and unstable relationships between others, just as we first encountered with the initial presentation of the sunrise melody. A lack of synchronization between metric accents across levels is partly responsible for the sense of fluidity often ascribed to Ravel’s music; because his metric formulations are never really “grounded,” musical events appear to be in a constant state of evolution, a process that Horlacher perceives as marking “a flow of time” in contrast to a periodic articulation of time.[31]

In general terms, this technique is not unique to Ravel. Kramer provides several musical examples from the western classical tradition to support his view that meter exists on multiple levels, “some of which are regular and some not.” He explains, “Because we perceive several levels simultaneously, we are quite capable of understanding irregularities that are subsumed into deeper-level regularities.”[32] Still, what sets Ravel apart from the common-practice era composers on which Kramer focuses is the fact that his metric irregularities are not heard in relation to a metrically regular surface level (as we have seen).[33] Akin to Horlacher’s remarks on Stravinsky, I would propose that Ravel’s creation of a fluctuating metric hierarchy cannot be viewed as deviant in relation to established periodicity; rather, this metric condition is inherent to Ravel’s compositional aesthetic just as metric irregularity gains a “normative status independent of a fixed point of reference” in Stravinsky.[34]

The absence of metric anchoring is not the only feature that contributes to a fluid, temporal flow in Daphnis. Ravel’s conception of meter as supple certainly seems to have impacted his musical setting of the lovers’ reunion, the narrative highlight and focal point of dramatic resolution. Despite the fact that much of the preceding drama has revolved around Daphnis’s painful separation from Chloé, it is intriguing that Ravel chooses to make light of this moment by dwelling on the lovers’ ecstasy for a mere five measures before proceeding to other aspects of the narrative. Even though Ravel changes the meter from 3/4 to 9/8 to “prolong” the musical duration of their embrace in m. 55, we might not expect this long-awaited resolution to be treated as a transitory phenomenon, let alone one characterized by metric instability (although by now, the listener might well be able to anticipate Ravel’s preferred metric state).

In the larger scheme of things, it is neither sunrise, nor Chloé’s return, but the acknowledgement of Pan (m. 70) that receives the strongest structural accent as conveyed by hypermetric regularity, which coincides with a return to the tonic. Structural emphasis on Pan’s role as deus ex machina rather than Chloé’s return supports the previously observed hierarchical trinity between Pan and the lovers, while reinforcing the point that Daphnis and Chloé are a couple blessed and protected by Pan. The distinct pace of each temporal progression and its inter-weaving—natural, narrative, metric—illuminates Jankélévitch’s observation of how Ravel’s listener is constantly challenged to adjust his/her expectations of musical continuity. In this respect, the Sunrise Scene provides strong musical resonance for Jankélévitch’s insights given Pan’s association with a higher-level state of metric stability, and nature’s explicit depiction through instability; nature’s final tribute to Pan emphasizes an enduring, primordial divinity in contrast to its own fluctuating identity.

* * *

Even as we perceive a lack of synchronicity between the three temporal frames, the one gesture that permeates each is the arabesque motif. By aligning itself with various events—daybreak, birdsong, passing shepherds—this intricate figure unites the multitude of sensations enmeshed within this tableau vivante. The motif’s evocation of rippling streams and (through stasis) the enduring sun provides an obvious aural counterpart to the dramatic setting. At the same time, its signification of water invites an association with Daphnis’s subconscious through Freudian extension, and thus serves to fuse the realms of nature and human emotion. We experience the expressive intensity of this elision at a critical dramatic juncture, a moment so overpowering that it ruptures the formal frame established at the opening. This frame initially served to segregate natural and human realms with sunrise having taken place at the end of the introduction before shepherds entered the scene to find and awaken Daphnis. The closing frame is also reserved for nature and its homage to Pan. But in the central phrases, Daphnis’s subconscious anxiety only remains dormant for so long: at the moment of his awakening, his conscious awareness of Chloé’s absence breaks the frame. The motif now surpasses all barriers—formal, textural, subconscious—to unleash his overwhelming distress as echoed by nature.

Like Pan, Daphnis has strong associations with nature, especially in Longus’s original novel where he is discovered abandoned as a baby in the woods. Even as we can well understand Ravel’s interest to emphasize this link, a question that still lingers concerns his decision to explore Daphnis’s inextricable relationship to nature and divinity through a motif, which at first glance appears to be little more than a fleeting ornament. Why would Ravel choose to narrate this episode—including its pastoral setting and the drama’s climax—through a complicated decoration that maintains an ambiguous metric identity and a volatile textural presence? While an in-depth answer to this question takes us far beyond the reach of this paper, I would like to mention in closing that Ravel’s decision to use the arabesque motif as a structural element gives us several unique insights into his compositional and aesthetic ideals.

For instance, a recurring feature of Ravel’s metric style is the construction of a metric state that we characterized as a “stable-instability.” We saw how various pulses embedded within the arabesque motif came to form simultaneous dissonant and consonant relationships with other pulses on distinct metric levels. In a different manifestation of the same metric condition, we studied how regularity on higher metric levels subsumed the irregular activity of the arabesque motif and other pulses on low levels. The supple and dynamic qualities of meter promoted through such an ambiguous construction compel us to participate in a different mode of listening; one that does not take periodicity as a norm, and moreover, one that does not perceive meter as a “top-down” experience. In the Sunrise Scene, at least, we have seen how much of this episode’s metric complexity may be attributed to rhythmic activity at the lowest level, a feature that finds resonance in London’s belief that, “meters do not exist apart from rhythmic surfaces that initiate and sustain them.”[35] On this note, I believe that Mark Butler’s comments on electronic dance music create an unusual yet accurate analogue to Ravel’s achievements in this scene: “rhythm begins to seem not so much like a foreground phenomenon embellishing some deep background structure, but rather as a structurally significant element in its own right.”[36]

Finally, it is culturally and historically significant that Ravel chose to narrate this episode through a musical feature that approximates visual arabesque. I have shown elsewhere how fin/debut-de-siècle Paris was preoccupied with exploring arabesque’s physical and expressive attributes across a range of artistic media.[37] As a type of decoration, arabesque had long participated in an historical debate that contested the structural and semantic significance of ornament in western thought: is ornament independent of structure? Can it mean anything in and of itself? Is it merely a superficial manifestation of beauty? Following the Parisian Rococo revival of the mid-nineteenth century, Ravel, and many of his contemporaries, created a response to these questions that clearly celebrated ornament.[38] Certainly, his treatment of the arabesque motif in this scene indicates his position on the matter. Ravel’s careful monitoring of the motif in the frame, and his deliberate transgression of this boundary at a crucial expressive moment, reveals his interest to subvert the conceptually hardened distinction between structure and ornament. His playful manipulation of this boundary suggests a willingness to re-conceptualize musical structure, particularly the distinction between background and foreground. Most importantly, Ravel’s notion of fluidity allowed him to re-define our engagement with those parameters that mark music’s passage through time.