Harmonische Mehrdeutigkeit und ihre Gründe
Andreas Moraitis
Wenn von harmonischer Mehrdeutigkeit und den daraus resultierenden Schwierigkeiten für die Analyse die Rede ist, dürfte der Gedanke an Musik der Spätromantik – mit Richard Wagners Tristan als Paradigma –kaum zu unterdrücken sein. Indessen stellte schon die Harmonielehre des frühen 18. Jahrhunderts ihren Begründer Jean-Philippe Rameau vor Probleme, die nicht als Folge eines noch ungenügenden Entwicklungsstands der Theorie mißverstanden werden dürfen, sondern als Ausdruck prinzipieller, die Wahrnehmung, Auffassung und Interpretation musikalischer Zusammenhänge betreffender Gegebenheiten anzusehen sind. Anhand einiger Beispiele harmonisch ambivalenter Konstellationen unterschiedlichen Typs wird gezeigt, daß Mehrdeutigkeit in ihrer manifesten Form auf dem Konflikt von Bedeutungsebenen (historischer, perzeptueller oder sprachlicher Art) beruht, die sich nicht notwendig erst in problematischen Situationen konstituieren, sondern wenigstens zum Teil permanent vorhanden sind. Dementsprechend kann der Eindruck von Eindeutigkeit auf die Kohärenz der für die Rezeption maßgeblichen Kontexte zurückgeführt werden: Musiktheoretische Begriffe, die aus solchen ›eindeutigen‹ Sachverhalten abgeleitet sind, verlieren an Relevanz oder werden unbrauchbar, sobald das konstitutionelle Gefüge in Bewegung gerät.
Daß Begriffe wie ›Harmonie‹, ›Akkord‹, ›Stufe‹ oder ›Funktion‹ sich kaum verbindlich explizieren lassen, hängt nicht nur mit der Vielfalt harmonisch gebundener Stile und der Existenz unterschiedlicher theoretischer Traditionen zusammen, sondern auch mit der Struktur der zu beschreibenden Realität: kompositioneller Kontext, Tonsystem und Notenschrift, akustisches und physiologisches Substrat, das Hörbewußtsein und schließlich die musiktheoretische Sprache selbst sind Bereiche, mit denen jene Begrifflichkeiten direkt oder mittelbar in Verbindung stehen, ohne daß das Netz der Beziehungen durch ein einfaches und unmißverständliches Schema zu beschreiben wäre. Die daraus resultierende Vagheit des Bezeichnens kann als harmlos gelten, solange die Verständigung im Rahmen eines musiktheoretischen »Sprachspiels« (Ludwig Wittgenstein) gewährleistet bleibt.[1]
Versagt dieses Sprachspiel (was nicht ausschließlich, aber häufig dann geschieht, wenn Vertreter unterschiedlicher Fachrichtungen oder Schulen aufeinander treffen), so sind die Gründe oft auf der begrifflichen Ebene zu suchen: Wer etwa einen ›Akkord‹ vor allem mit Hinblick auf seine satztechnische Verwendung bewerten möchte, wird bei der Analyse bestimmter musikalischer Stile und Situationen wahrscheinlich zu anderen Einschätzungen gelangen als derjenige, der seinen Akkordbegriff hauptsächlich unter akustischen oder psychologischen Gesichtspunkten entwickelt hat. Die Verschiedenheit der Deutungen wäre in solchen Fällen Folge der semantischen Differenzen und sollte, sobald diese aufgezeigt sind, nicht mehr als Widerspruch erscheinen.
Allerdings wird die Möglichkeit unterschiedlicher Auffassungen darüber, was für die Analyse eines harmonischen Sachverhalts maßgeblich sei, durch die erwähnte Vielschichtigkeit der musikalischen Realität nicht nur begünstigt, sondern auch unterminiert: Je genauer wir nämlich unsere Begriffe auf den zu untersuchenden Gegenstand fokussieren, desto kleiner gerät der erfaßte Ausschnitt, desto unvollständiger das Bild.
Die Koexistenz einander ergänzender theoretischer Ansätze scheint somit fast unvermeidlich. Den durch sie manifestierten, strukturell bedingten Formen von ›Mehrdeutigkeit‹ stehen Fälle perzeptueller Ambiguität als vermeintlich autonome Instanzen gegenüber. Jedoch erlaubt es das spezifische Verhältnis von Begriff und Theorie auf der einen und dem musikalischen ›Hören‹ auf der anderen Seite nicht immer, Wahrnehmung und intellektuelle Deutung zuverlässig auseinanderzuhalten. Im folgenden soll zunächst ein allgemeiner theoretischer Zugang zu der Problematik skizziert werden, dessen Anwendung anschließend an einigen paradigmatischen Fällen zu erproben sein wird.
* * *
Vereinfachend könnte man den Begriff einer musikalischen ›Harmonie‹ als Katalog von Variablen auffassen, deren Werte sich im individuellen Fall mehr oder weniger erfolgreich konkretisieren lassen. Solche Variablen wären je nach Art der angewendeten Theorie etwa ›Grundton‹, ›Klanggeschlecht‹, ›Stufe‹, ›Funktion‹ usw. Darüber hinaus können einzelne Töne als ›Leitton‹, ›Dominantseptime‹, ›neapolitanische Sexte‹ u. dgl. charakterisiert werden. Schon diese wenigen Beispiele zeigen, daß sich die ›Bedeutung‹ der zu bewertenden Sachverhalte relativ zu einer Reihe von Bezugssystemen konstituiert: Ein einfaches Bezugssystem wäre bereits der ›Akkord‹, in dessen Kontext wesentliche Eigenschaften der Einzeltöne entstehen, der aber seinerseits beispielsweise in die Klasse der leitereigenen Akkorde eingestuft, aber auch als Glied einer Kadenz oder eines Sequenzmodells identifiziert werden kann. Die Harmonienfolgen wiederum lassen sich hinsichtlich ihrer Beziehung zum Fundus der stilistischen Topoi bewerten usw. Jeder zu analysierende Sachverhalt ist also schon insofern mehrdeutig, als er verschiedenen Bezugssystemen oder Kontexten zugleich angehört. Diese Systeme können hierarchisch aufeinander aufgebaut sein, aber auch – wie sich an der Relation von ›vertikalen‹ und ›horizontalen‹ Ereignissen besonders gut ablesen läßt – ›quer‹ zueinander stehen. Schlägt die Einordnung des zu analysierenden Sachverhalts in einen der Kontexte fehl, kann sich ein solcher nicht konstituieren oder treten mehrere Kontexte miteinander in Konflikt, so vermag daraus – so jedenfalls die hier favorisierte These – Unbestimmtheit bzw. Mehrdeutigkeit im engeren Sinn zu resultieren.
Die verminderten Septakkorde zu Beginn des vierten Satzes von Edward Elgars Violoncellokonzert gehören in der Terminologie Arnold Schönbergs zu den »vagierenden Akkorden«, da sie in einer Vielzahl von Tonarten und Situationen einsetzbar sind: Schönberg führt in seiner Harmonielehre allein für die dominantische Verwendung eines solchen Akkords 44 Möglichkeiten an.[2] Daß das Auftreten des verminderten Septakkords am Satzanfang temporär nicht nur die Identifikation, sondern bereits die Konstitution einer Tonart verhindert, mag also plausibel erscheinen.[3]
Beispiel 1: Edward Elgar, Cello Concerto op. 85, IV. Satz, T. 1-8, Auszug
Indessen kann auch ein gewöhnlicher Dreiklang einer ganzen Reihe von Tonarten angehören, ohne daß sein Erscheinen zu Beginn des Stücks Unbestimmtheit auslösen müßte. Hier kommt zweifelsohne die Erfahrung – und damit das System der stilistischen Konventionen – ins Spiel, denn in den meisten dur-moll-tonalen Kompositionen nicht-rezitativischen Charakters, die mit einem Dreiklang ohne beigefügte Dissonanz beginnen, ist dieser Dreiklang mit der Tonika identisch.
Um aber ein tonales Zentrum bilden zu können, muß der Akkord selbst ›zentriert‹ sein (Rameau sprach vom centre harmonique[4]), also einen Grundton besitzen. Eine empirische Methode, mit deren Hilfe sich Grundton, Terz und Quinte von Dur- oder Molldreiklängen in beliebiger Stellung und Lage zuverlässig identifizieren lassen, hat Roland Mackamul im ersten Band seines Lehrbuchs der Gehörbildung beschrieben. Die Bestimmung der Intervallqualität erfolgt dabei durch Singen oder Vorstellen charakteristischer Motive; Beispiel 2 skizziert eine modifizierte Version des Verfahrens.[5]
Beispiel 2: ›Operationalisierung‹ von Dreiklangsintervallen (* = nach Mackamul)
Der auf diese Weise zu ermittelnde Grundton sei im folgenden ›operationaler Grundton‹ bzw., sofern er sich auf Akkorde bezieht, auch ›primärer Grundton‹ genannt.[6] Er ist noch kein harmonischer Grundton; anscheinend kann der primäre Grundton initialer Dreiklänge aber in einem Modus der Transferenz auf den nächsthöheren Kontext übertragen werden.
Verminderte Septakkorde verfügen dank ihrer symmetrischen akustischen Struktur sowie des Fehlens der reinen Quinte über einen derartigen Grundton nicht; sie wären also auch dann, wenn sie normativ an Satzanfängen erschienen, zur Festlegung der Tonart ungeeignet. Der aus der Notation zu erschließende ›Grundton‹ eines verminderten Septakkords (z. B. fis bei dem Akkord fis-a-c'-es') ist bloß ein ›nomineller Grundton‹, der sich nicht auf die Wahrnehmung des Akkords, sondern auf seine logische[7] und akustische Struktur bezieht.
Beispiel 3: Deutungen des kadenzierenden Quartsextakkords
Beispiel 3 zeigt verschiedene Interpretationen des sogenannten kadenzierenden Quartsextakkords. Die ›klassische‹ Stufentheorie leitete diesen Akkord trotz seines Vorhaltscharakters und der in der Regel deutlich wahrnehmbaren dominantischen Wirkung von der I. Stufe ab, während die funktionstheoretische Schreibweise 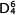
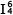
Daß die musikalische Realität noch andere Optionen bereithält, mag das folgende Beispiel illustrieren. Am Schluß des Bach-Chorals Wenn wir in höchsten Nöten seien erscheint unter der Antepaenultima ein Akkord, der – wäre nicht H, sondern d der Baßton – dem eben behandelten Vorhaltsquartsextakkord entspräche. Seine musikalische Wirkung ist diesem sehr ähnlich, obwohl es sich formell um einen tonikalen Sextakkord handelt. Wenn wir diesen Akkord unwillkürlich mit dem kadenzierenden Quartsextakkord in Verbindung bringen, so scheint dies auf der Assoziation des Gehörten mit einem internalisierten Schema zu beruhen, wäre also in moderner Terminologie als ›top-down‹-Prozeß zu interpretieren. Zugleich aber könnte man von einer Dissoziation des Akkords und der Installation eines Subkontextes zwischen den drei oberen Stimmen sprechen.[9]
Beispiel 4: Johann Sebastian Bach, Choral Wenn wir in höchsten Nöten seien (BWV 432), Schluß
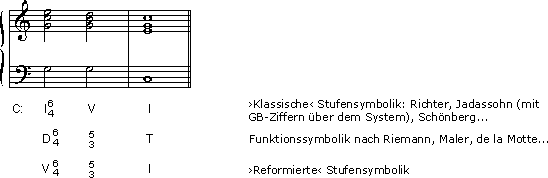
Die Deutung des auf der vierten Stufe der Skala konstruierbaren, in heutiger Terminologie als ›Subdominante mit sixte ajoutée‹ bezeichneten Quintsextakkords hat bekanntlich schon Jean-Philippe Rameau erhebliche Probleme bereitet. Rameau betrachtete den Akkord seit 1726 als sous-dominante, sofern er der ersten Stufe vorausging, hingegen als dominante, falls ihm die V. Stufe folgte.[10] Damit wurde im zweiten Fall das Oktaväquivalent der Sexte zur basse fondamentale, also zum harmonischen Grundton im Sinne Rameaus. Dem kommt die stufentheoretische Schreibweise 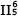
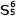
Beispiel 5: ›Rameaus‹ Quintsextakkord
Dabei würde es sich nach der hier verwendeten Terminologie um einen sekundären Grundton handeln. Die Anwendung des oben beschriebenen Tests auf den Durquintsextakkord liefert kein eindeutiges Ergebnis. Je nach Stimmaufteilung bzw. -lage und dem gewählten Modus der Operationalisierung können sowohl die Sexte als auch der Baß mehr oder weniger deutlich als primäre Grundtöne gehört werden: Der Akkord ist intrinsisch ambivalent.[11] Bei der Mollform läßt sich eine deutliche Tendenz zum Baß beobachten, die aber infolge der Dissonanzspannungen ebenfalls zu keiner sehr stabilen Strukturierung führt.
Die Beziehung des leitereigenen Quintsextakkords der IV. Stufe zu demjenigen der Doppeldominante ist also nicht mit dem Hinweis auf die Korrespondenz primärer Grundtöne zu erklären;[12] statt dessen scheinen eine Reihe weiterer Faktoren – insbesondere das Vorhandensein gemeinsamer Töne, aber auch die identische Intervallstruktur und das analoge Stimmführungsmodell (s. u.) – von Belang zu sein. Doch kann wiederum eingewendet werden, daß dies gleichermaßen das Verhältnis des doppeldominantischen zu dem subdominantischen Akkord betrifft, ohne daß wir geneigt wären, den ersteren als Präzedenzfall einer mehrdeutigen Harmonie zu betrachten. Den Ausschlag gibt in diesem Zusammenhang wohl der Umstand, daß sich die 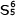
Das Prinzip der gemeinsamen Töne vermag trotz der eben genannten Einschränkung den an der Einheit des ›Akkords‹ orientierten Funktionsbegriff ad absurdum zu führen. Die Frage etwa, ob ein Undezimenakkord wie G-f'-a'-c'' (in C-Dur) eher als Dominante oder doch als Subdominante über einem Orgelpunkt aufgefaßt werden soll, dürfte kaum definitiv zu entscheiden sein, da sowohl die ›authentische‹ als auch die ›plagale‹ Komponente seiner tonikalen Auflösung musikalisch real sind. Unscheinbarer als solche ›bifunktionalen‹ Akkorde wirken ›homonyme‹ Klänge, wie etwa die VI. Stufe in Molltonarten: Funktionstheoretisch ist diese bekanntlich bei vorausgehender Subdominante als deren Parallele zu klassifizieren, im Rahmen eines Trugschlusses aber als Tonikagegenklang. ›Mehrdeutig‹ sind hier weniger die Klänge in ihrer spezifischen Umgebung als ihr abstraktes akustisches, notenschriftliches oder (je nach verwendeter Theorie) auch sprachliches Pendant (»die VI. Stufe«) – betrachtet mit Bezug auf die Gesamtheit der untersuchten Situationen.
Die durch Rameau vorgenommene Beschränkung der harmonischen Relationen auf die Quintverwandtschaft[13] hatte bekanntlich zur Folge, daß Sekundfortschreitungen wie die Wendung IV-V umständlich mit Hilfe des double emploi begründet werden mußten; dem entspricht die Interpolation »scheinbarer Fundamentschritte«[14] in der späteren Stufentheorie. Die Annahme solcher neben den manifesten Klangverwandtschaften wirksamer indirekter Quintenbeziehungen ist auch aus heutiger Sicht nicht ganz von der Hand zu weisen. Doch sollte zusätzlich die räumliche Nachbarschaft von Tönen (gemäß dem gestaltpsychologischen ›Prinzip der Nähe‹) als ein die Plausibilität der Fortschreitungen förderndes Moment in Betracht gezogen werden. Daraus ergeben sich freilich wiederum Doppeldeutigkeiten unterschiedlicher Art; so läßt sich der Klang e-g-h in bezug auf eine C-Dur-Tonika sowohl als leitereigene Obermediante wie auch als »»Leittonwechselklang«« beschreiben.[15] Die Alternative ist vermutlich nicht bloß eine Frage der Auffassung oder der gewählten Theorienkonstruktion: Vielmehr könnte sie bereits auf elementaren (›bottom-up‹-)Mechanismen der auditiven Verarbeitung beruhen.
Wie am Beispiel des Vorhaltsquartsextakkords deutlich geworden ist, setzt die Klassifikation von Harmonien die Unterscheidbarkeit ›harmoniefremder‹ und ›harmonieeigener‹ Töne voraus. Daß die Auffassungen bezüglich der Frage, welche Töne als Akkordbestandteile und welche als Zutat zu betrachten seien, historisch variabel ausfielen, läßt sich an den komponierten Werken wie auch an Theoretikeraussagen ablesen. Doch während sich viele Akkordbestandteile ursprünglich aus regulierten Dissonanzformen entwickelten, ging ihre ›akzidentelle‹ Komponente doch nicht ganz verloren: So konnte die Dominantseptime, welche noch im frühen 18. Jahrhundert als anticipatio transitus definiert worden ist, auch nach ihrer Emanzipation zum harmonieeigenen Ton in Gestalt einer nachschlagenden Septime verwendet werden; analog waren Nonen oder Undezimen noch im 20. Jh. als Vorhalte bzw. Vorausnahmen komponierbar. Die in Werken der Spätromantik zu beobachtende Häufung solcher ›hybrider‹ Töne bedingt eine weitere Schwierigkeit der harmonischen Analyse.
Der satztechnische Begriff der kontrapunktischen Struktur läßt sich nicht nur zur logischen Kategorie der Konstruktion, sondern auch zur psychologischen des Bewegungsmusters in Beziehung setzen.
Beispiel 6: ›Phrygischer‹ Halbschluß
Die in Beispiel 6 dargestellten, mit der eben besprochenen Harmonienfolge verwandten Kadenzen wären unter diesem Gesichtspunkt als gleichartig zu klassifizieren, obwohl sie funktionstheoretisch unterschiedlich zu deuten sind; in dieser Hinsicht ist die Stufensignatur (wenn auch wohl zufälligerweise) der Funktionssymbolik überlegen. Historisch betrachtet ist die erste Folge Vorgängerin der zweiten, welche sich erst in der Frühklassik als Standardform etablierte; in dur-moll-tonaler Musik sind die beiden Kadenzformeln von durchaus kongruenter Bedeutung.[16] Andererseits kann dem übermäßigen Sextakkord ein dominantischer Charakter nicht abgesprochen werden; dieser dürfte allerdings weniger durch die kontrapunktische Form als durch die Präsenz von Leitton und Septime determiniert sein. Ob die Annahme eines ›verschwiegenen‹ Grundtons, wie sie das Funktionssymbol zum Ausdruck bringt, auf eine Option der Wahrnehmung verweist, einen latenten Kausalzusammenhang widerspiegelt oder bloß musiktheoretischem Systemzwang folgt, bleibt eine der Klärung bedürftige Frage.[17]
Daß Tondistanzen im Vergleich zu Intervallen im herkömmlichen Sinn weit unempfindlicher gegenüber Veränderungen sind, läßt sich besonders gut am Beispiel von Sequenzmodellen verdeutlichen. So beeinträchtigt die bei Quintfallsequenzen wie der in Beispiel 7 wiedergegebenen zwangsläufig auftretende verminderte Quinte die Kohärenz des musikalischen Verlaufs keineswegs, obwohl sie in akustischer und klanglicher Hinsicht mit einer reinen Quinte wenig gemeinsam hat: Offenbar spielt das Konsonanzempfinden hier eine untergeordnete Rolle. Die aus der Konfrontation des nicht-äquidistanten diatonischen Systems mit dem äquidistanten Zwölftonsystem resultierende Halbtondifferenz könnte – in Analogie zu den entsprechenden akustischen Phänomenen – als ein ›logisches Komma‹ bezeichnet werden.[18]
Beispiel 7: Arcangelo Corelli, Sonata da Chiesa op. 3, Nr. XI, I. Grave, T. 104-123
Eine in diesem Zusammenhang bemerkenswerte Stelle findet sich im zweiten Teil des Sanctus aus Wolfgang Amadeus Mozarts Krönungsmesse. Nach dem in T. 23 erscheinenden g-Moll-Akkord beginnt eine Quintfallsequenz abzulaufen, deren Komponenten ab T. 24 durch die Harmonien A-Dur, d-Moll, G-Dur und C-Dur markiert sind. Überraschenderweise scheint der Ausgangspunkt der Sequenz aber nicht im 24., sondern bereits im 23. Takt, also bei dem erwähnten g-Moll-Akkord, zu liegen, obwohl die Grundtöne g und a nicht im Quint-, sondern im Sekundabstand stehen. Dabei mag die charakteristische Konsonanz-Dissonanz-Verkettung im Sopran eine Rolle spielen; auffällig ist jedoch der Umstand, daß der Baß zwischen den Takten 23 und 24 mit den Tönen g und cis tatsächlich eine – wenn auch verminderte – Quinte ausführt, die (obwohl sie bloß die Terz der A-Dur-Harmonie anzielt) in den Verlauf der nachfolgenden Sequenz integriert wird.[19]
Beispiel 8: Wolfgang Amadeus Mozart, Krönungsmesse (KV 317), Sanctus, T. 18-29, Ausschnitt
Als ein weiterer Grund für die Mehrdeutigkeit von Harmonien kann die Existenz unterschiedlicher hierarchischer Ebenen genannt werden. So wird die Analyse des erwähnten Modells der Quintfallsequenz mittels der herkömmlichen Chiffrensysteme dem Umstand nicht gerecht, daß die Beziehungen zwischen den aufeinanderfolgenden Harmonien dabei ebenso wichtig sind wie ihre Subordination unter ein tonales Zentrum oder ihr Bezug zu einer diatonischen Skala. Dem würde wiederum durch die Theorie Rameaus, welche sich ja auf zweigliedrige Kadenzen beschränkte, Rechnung getragen. Schließlich müßte eine umfassende Deutung auch die lineare Beziehung jeder Harmonie zur jeweils übernächsten berücksichtigen usw.
Die damit indirekt angesprochene Möglichkeit, bestimmte Elemente einer harmonischen Progression als Interpolationen aufzufassen, verweist auf Simon Sechters Konzept der Prolongation, das durch dessen Enkelschüler Heinrich Schenker weiterentwickelt und in den Rang eines universalen, die Struktur ganzer Sätze bestimmenden Prinzips erhoben worden ist. Zu den im Zusammenhang mit der Theorie und Methode Schenkers noch zu lösenden Problemen gehört sicherlich dasjenige der Übertragbarkeit lokaler Determinanten auf eine globale Ebene.[20] Sieht man von dem für Schenkers spätere Lehre allerdings wesentlichen Aspekt der Stimmführung ab, so ist die Möglichkeit derartiger Übertragungen auch von der konventionellen Musiktheorie anerkannt worden: So dürfte die Bedeutung des ›Halbschlusses‹ am Ende des ersten Teils eines Suitensatzes für die Formbildung unumstritten sein, obwohl die betreffende Dominante auch durch eine authentische Kadenz erreicht werden kann, die sie als lokale Tonika qualifiziert.
Normalerweise ›unverdächtige‹ Akkorde können demnach mehrdeutig bzw. vage werden, sobald sie in den Kontext von Ausweichungen oder Modulationen geraten. Ob eine bestimmte Harmonie schon zur neuen Tonart gehört oder noch zur alten, läßt sich aufgrund der Prozessualität musikalischen Hörens nicht immer klären; trotzdem besitzt die ›unbekannte Zone‹ einer Modulation in der Regel keinen ›atonalen‹ Charakter.
Beispiel 9: Enharmonische Modulation
Im Unterschied zu solchen ›Sowohl-als-auch-Fällen‹ könnte man mit Hinblick auf enharmonische Modulationen wie die in Beispiel 9 skizzierte von ›Entweder-oder-Fällen‹ sprechen. Die bei der Umdeutung des Dominantseptakkords in den übermäßigen Quintsextakkord vollzogene, mit einer Transformation sämtlicher Konsonanzen und Dissonanzen in ihr Komplement verbundene Metamorphose des tonalen Bezugssystems ist so radikal, daß ein Vergleich mit Formen perzeptuellen Gestaltwandels naheliegt, wie sie im visuellen Bereich bei der Betrachtung sogenannter Kippfiguren auftreten.[21] Allerdings lassen sich auch Unterschiede benennen: So erfolgt das Umschlagen der Bedeutung bei der Harmonienfolge nicht spontan, es wird vielmehr durch den musikalischen Verlauf evoziert; darüber hinaus trägt die nicht eingelöste Dominantsept-Implikation zu einem trugschlußartigen Charakter der Wendung bei.
Beziehungen zwischen der Kategorie des Klangs und derjenigen der Harmonie sind in der Geschichte der Musiktheorie immer wieder postuliert worden. Auf die zahlreichen Versuche, die harmonische Tonalität mit dem Naturklang in Verbindung zu bringen, soll an dieser Stelle nicht eingegangen werden. Statt dessen sei an den Umstand erinnert, daß sich die von Akkorden oder Intervallen ausgelöste Klangempfindung im Unterschied zur harmonischen Funktion durchaus unabhängig von der Existenz einer bestimmten Umgebung konstituieren kann: Ein Dreiklang ist auch dann ein Dreiklang, wenn er exemplarisch am Klavier angeschlagen wird – hingegen bedarf der gleiche Dreiklang, um ›Subdominante‹ zu werden, eines geeigneten harmonischen Milieus. Umgekehrt vermögen die in den musikalischen Verlauf integrierten Klänge einen Teil ihrer Souveränität zu bewahren: Wir erkennen den ›Dreiklang‹ in der Regel auch dann, wenn er als Subdominante exponiert ist. Selbst in einem so kritischen Fall wie demjenigen des Tristanakkords erweist sich die Klanggestalt als eigenständige und per se durchaus eindeutige Erscheinung.[22]
Beispiel 10: Richard Wagner, Tristan und Isolde, Einleitung zum I. Akt, T. 1-3, Auszug
An der einzigartigen Wirkung der ersten Takte des Tristan-Vorspiels scheinen nahezu alle bislang genannten Faktoren beteiligt zu sein: die klangliche Vagheit des ersten Akkords, der Vorhaltscharakter des ›primären Grundtons‹ gis, das Vorhandensein gemeinsamer Töne mit mehreren, funktional disparaten Harmonien, die Strebetendenz der Linien, der Verzicht auf eine mögliche Auflösung in die Dominante von es-Moll, dafür die Umdeutung des potentiellen Grundtons b' zum Vorhalt ais', dessen interpolierende Funktion und anderes mehr. Die Harmonienfolge läßt nicht glaubhaft auf ein elementares Modell reduzieren. Insbesondere betrifft dies den für die Plausibilität der Auflösung unerläßlichen Ton ais'. Bei umgekehrter Bewegungsrichtung ergibt sich bemerkenswerterweise eine ähnliche Situation.
Beispiel 11: Richard Wagner, Tristan und Isolde, Einleitung zum I. Akt, T. 2-3, Irreduzibilität der Auflösung. Oben: Original, unten ›Umkehrung‹ mit Reduktion
Dies könnte auf einer Deformation der perzeptuellen Koordinatensysteme beruhen, wie sie möglicherweise auch für die im Zusammenhang mit der sogenannten ›scala enigmatica‹ auftretende ›akustische Täuschung‹ verantwortlich ist.[23]
Beispiel 12: Die scala enigmatica
Abbildung 1: Optische Täuschung (die Strukturen sind deckungsgleich)[24]
Auch wenn die solchen Effekten zugrundeliegenden Mechanismen bis heute weitgehend ungeklärt sind, müßte die Irreduzibilität des Tristan-Anfangs unter der Prämisse, daß das supponierte Modell durch ein anderes Raster wahrgenommen wird als das Original, zumindest nicht mehr verwundern.
* * *
Als Fazit dieser fragmentarischen Ausführungen ließe sich festhalten: Musikalische Harmonik kann, wie Musik überhaupt, als ein multikontextuelles Phänomen beschrieben werden; schon der einfachste zu analysierende Sachverhalt ist in gewissem Sinne mehrdeutig und mit präzise abgegrenzten Begriffen nur unzulänglich zu beschreiben.[25] Die unterschiedlichen Kontexte können einander verstärken oder hemmen, ihre Strukturen und Inhalte modifizieren, zu übergeordneten Zusammenhängen verschmelzen oder in Subkontexte zerfallen. Das musikalische Hören und die Theorienbildung im ganzen erweisen sich in dieser Hinsicht als durchaus verwandte Aktivitäten – wenn auch das Medium der musiktheoretischen Sprache über sich hinauswachsen müßte, um der Mannigfaltigkeit ästhetischer Prozesse zu genügen.
Anmerkungen
Wittgenstein 1969, passim. Auch die Netzmetapher, welche die Struktur der Wirklichkeit in vielerlei Hinsicht angemessener zu beschreiben scheint als die klassischen generativen Konzepte, geht auf Wittgenstein zurück (vgl. ebd., 324). | |
Vgl. Schönberg 1922, 237ff. | |
Strenggenommen hat die zitierte Einleitung eine modulierende Funktion: Der III. Satz steht in B-Dur und endet auf der Dominante F. Es wäre daher möglich, den ersten Akkord des IV. Satzes als Doppeldominante von B-Dur zu chiffrieren – was allerdings am Habitus der Passage nichts ändert. | |
Rameau 1722, 127. | |
Vgl. Mackamul 1993, 75. Mackamul empfiehlt zur Bestimmung des Grundtons das Singen eines Quartpendels; da mit diesem jedoch leicht ein Funktionswechsel assoziiert wird, sei hier den Dreiklangsbrechungen der Vorzug gegeben. Die Methode funktioniert auch bei Dominantseptakkorden (von der Septime aus wäre dann eine Akkordbrechung abwärts zu singen), allerdings scheint die Vorstellung der plausibelsten Auflösung zu einer nachfolgenden tonikalen Harmonie das effizientere Verfahren darzustellen. Der Verfasser bezieht sich hier und im folgenden auf Erfahrungen aus dem Gehörbildungsunterricht, die durch eine systematische musikpsychologische Studie zu ergänzen wären. Die Operationalisierung ist im übrigen kein zirkuläres Verfahren, da sie nicht bloß auf dem Strukturvergleich, sondern auch auf der Wahrnehmung spezifischer Qualitäten beruht. Sie läßt sich auf Melodietöne ebensogut anwenden wie auf Akkordtöne. | |
Die ›primären Grundtöne‹ sind nicht mit den sogenannten Residualtönen zu verwechseln, da die letzteren zwar bei Dur-, nicht jedoch bei Molldreiklängen (bzw. diesen entsprechenden Sinuskomplexen) mit dem Dreiklangsgrundton zusammenfallen. Die Operationalisierung ist hingegen unabhängig vom Klanggeschlecht möglich, ein Mollproblem tritt also nicht auf. | |
Der hier verwendete Begriff der ›logischen Struktur‹ bezeichnet die Konstruktion des Akkords, wie sie mit Hilfe des Zeichensystems der Notenschrift oder auch anderer formaler Repräsentationssysteme (z. B. einer Programmiersprache) ausgedrückt werden kann; er nimmt weder auf akustische Sachverhalte noch auf den Hörvorgang Bezug. Vgl. dazu Moraitis 1994, 147–158. | |
Gottfried Weber, der auf die Mehrdeutigkeit dieses Akkords bereits ausdrücklich hingewiesen hat, verwendete zwei übereinander stehende Zeilen von Stufensymbolen (teils mit arabischer Ziffer für die »I«), um die Alternative zu verdeutlichen (1821, 160); eine analoge Darstellung findet sich bei Simon Sechter (1854, 370). Sowohl Weber als auch Sechter verzichteten auf den Zusatz » | |
Das Prinzip der Oktavidentität wird hier anscheinend in Frage gestellt: Ist das h' des Soprans Vorhalt zu a', so kann es kein harmonieeigener Ton sein; umgekehrt wäre es abwegig, dem H des Basses einen Vorhaltscharakter zuzuschreiben. Daß dem Akkord eine tonikale Komponente zugesprochen werden kann, wie es ja auch bei dem ›echten‹ Vorhaltsakkord in manchen Fällen möglich ist, sei unbestritten (dies liefe dem hier vertretenen Ansatz im übrigen nicht zuwider). | |
Vgl. Rameau (1726), 38-66. Im Traité de l’harmonie (1722) wird der Begriff der sous-dominante noch nicht verwendet, jedoch findet sich im Anhang zum Kapitel über die cadence irrégulière eine Bemerkung, wonach der im Haupttext als Umkehrung charakterisierte Akkord (1722, 64) doch als Grundakkord interpretiert werden müsse (1722, 465 f. – dem entspricht schon die Abb. auf S. 65; vgl. dazu Hamburger 1955, 28-29). Dies wird allerdings nur für die cadence irrégulière reklamiert, während in allen anderen Fällen die Ableitung aus dem Septakkord maßgeblich sei: Die Idee eines double emploi zeichnet sich damit bereits deutlich ab. | |
Man vergleiche z. B. die auf dem Klavier angeschlagenen Formen f-a'-c''-d'' und f-c'-d'-a' unter Anwendung aller in Beispiel 2 dargestellten Möglichkeiten. Die Ambivalenz dürfte in erster Linie auf das Vorhandensein zweier reiner, miteinander ›konkurrierender‹ Quinten zurückzuführen sein, deren Wahrnehmung in Abhängigkeit von der jeweiligen Situation variabel ausfällt. Außer der Akkordstruktur und -lage sind wahrscheinlich auch die Dynamik, die Instrumentation und der Rhythmus für die Gewichtung der Akkordbestandteile von Bedeutung: Dies könnte (neben dem Einfluß stilistischer Normen) erklären, warum ein großer Durquintsextakkord im Jazz ohne weiteres als initiale Tonika fungieren kann, während er z. B. am Anfang des ersten Satzes von Ludwig van Beethovens Klaviersonate op. 31, Nr. 3 vage und ›unentschlossen‹ wirkt (vgl. zum letzten Fall Hamburger, a. a. O., 11ff.). | |
Dies gilt analog für den subdominantischen Status des Akkords mit ›substituierender‹ Sexte, bei dessen Durform die 6 als primärer Grundton dominiert (hier läge die Klassifikation als Subdominantparallele näher als die doppeldominantische Deutung). Sowohl die Mollform mit großer Sexte als auch der durch Verselbständigung eines Vorhalts entstandene ›Neapolitaner‹ lassen in dieser Hinsicht keine Affinität zur leitereigenen IV oder II erkennen – ein deutliches Indiz für die Relevanz des jenseits der ›primären‹ Ebene angesiedelten Geschehens. | |
Terzverwandtschaften hat Rameau ab 1737 zwar anerkannt, doch spielen sie in seinem System insgesamt eine untergeordnete Rolle. | |
Vgl. Sechter 1854, 18ff. | |
Vgl. Riemann 1929, 93ff. | |
Wird die Sexte diatonisch eingeführt und erst anschließend chromatisiert, tritt diese Verwandtschaft noch deutlicher zutage. Daß die ›Geschichte‹ des Akkords im Verlauf des Tonsatzes in diesem Fall die Kompositionsgeschichte zu rekapitulieren scheint, ist indes von geringerer Bedeutung als die Existenz solcher ›genetischer‹ Beziehungen im allgemeinen | |
Die Klassifikation des übermäßigen Sextakkords als ›italienischer Sextakkord‹ bietet nur scheinbar einen Ausweg, da sie lediglich die Nomenklatur, nicht jedoch die Theorie im Sinne einer den zu untersuchenden Gegenstand nicht nur benennenden, sondern auch interpretierenden und erklärenden Instanz betrifft. | |
Vgl. Anm. 7. | |
Wahrnehmungspsychologische Begriffe wie ›streaming‹ oder ›grouping‹ greifen hier zu kurz, da sich die Einheit der Quintenprogression auf einer abstrakteren als der linearen oder ›punktuellen‹ Ebene konstituiert. | |
Vor allem betrifft dies Schenkers Verfahren, die in kleinerem Maßstab oft gut wahrnehmbaren ›Züge‹ als sogenannte ›Urlinien‹ der Analyse ausgedehnter Kompositionen zugrunde zu legen (vgl. bes. Schenker 1956). | |
Im Gegensatz zur diatonischen Notierung, die keine Rücksicht auf funktionale Differenzen nimmt, bringt die enharmonische Schreibweise den Unterschied zutage: Paradoxerweise wird jedoch gerade sie oft als schwer verständlich angesehen, während die sich aus der Vielfalt möglicher Bedeutungsvarianten eines C-Dur-Akkords ergebenden Probleme nur selten Anlaß zu Besorgnis geben. | |
Vgl. Vogel (1962), 70–81, wo insbesondere auf die Takte 81–83 des Tristan-Vorspiels Bezug genommen wird: »Der Tristan-Akkord ist […] ein in sich gesättigter Klang, eine ›Klanggestalt‹. Daß er in einem bestimmten harmonischen Zusammenhang einer bestimmten Art der Weiterführung und Auflösung unterworfen ist, hat mit seiner ›Klanggestalt‹ zunächst nichts zu tun.« (80f.) Schon Ernst Kurth spricht von der »absoluten Klangwirkung« bzw. dem »Eigeneffekt des einzelnen Akkords« (1923, 297), der allerdings »immer zumindest durch sein Verhältnis zum vorhergehenden mit beeinflusst« werde (ebd.). Der Nebensatz impliziert nur scheinbar einen Widerspruch: Zwar kann der Klangcharakter durch das musikalische Geschehen beeinflußt, verfremdet oder sogar völlig überdeckt werden. Dies ändert aber nichts daran, daß bestimmte Klänge unverwechselbare Qualitäten besitzen, die in geeigneten musikalischen Situationen zweifelsohne auch zur Geltung kommen. Diese Individualität, und nicht die Unempfindlichkeit gegenüber Störungen, scheint Kurth zu meinen, wenn er vom »Eigeneffekt des einzelnen Akkords« spricht. | |
Die von Adolfo Crescentini erfundene scala enigmatica (relevant ist im vorliegenden Zusammenhang nur der aszendente Teil) wurde 1888 in der Gazzetta Musicale di Milano dem fachkundigen Publikum mit der Aufforderung vorgestellt, Vorschläge für eine Harmonisierung einzureichen. Giuseppe Verdi legte sie später dem Ave Maria aus seinen Quattro pezzi sacri zugrunde, wo sie als ›cantus firmus‹ sukzessiv durch alle vier Stimmen geführt wird. Vgl. dazu ausf. Conati 1978. | |
Links nach: Wikipedia, Artikel »Optische Täuschung« (http://www.wikipedia.org, [Stand: 04.09.2006]). | |
Der hier behandelte Begriff von Mehrdeutigkeit ist demzufolge weiter gefaßt als das Konzept der Ambiguität, wie es etwa von Leonard Meyer vertreten worden ist (vgl. Meyer 1956, 51ff.). Als Paradigma eines multikontextuellen Ansatzes mit umfassendem Anspruch kann die Analytik Jan LaRues gelten (LaRue 1992; zur Harmonik vgl. 39–68), auf die an dieser Stelle ausdrücklich verwiesen sei. |
Literatur
Beach, David (1967), »The Functions of the Six-Four-Chord in Tonal Music«, Journal of Music Theory 11/1, 2–31.
Conati, Marcello (1978), »Le Ave Maria su scala enigmatica di Verdi dalla prima alla seconda stesura«, Rivista italiana di musicologia 311, Vol. XIII, 280–311.
Mackamul, Roland (71993), Lehrbuch der Gehörbildung. »Bd. 1: Elementare Gehörbildung«, Kassel: Bärenreiter.
Moraitis, Andreas (1994), Zur Theorie der musikalischen Analyse, Frankfurt a. M.: Peter Lang.
De la Motte, Diether (31980), Harmonielehre, Kassel: Bärenreiter.
Hamburger, Paul (1955), Subdominante und Wechseldominante, Wiesbaden: Breitkopf & Härtel.
Jadassohn, Salomon (1895), Lehrbuch der Harmonie, Leipzig: Breitkopf & Härtel.
Kurth, Ernst (31923), Romantische Harmonik und ihre Krise in Wagners »Tristan«, Reprograf. Nachdr. der Ausg. Berlin: Hesse.
La Rue, Jan (21992), Guidelines for Style Analysis, Michigan: Harmony Park Press.
Maler, Wilhelm (41957), Beitrag zur durmolltonalen Harmonielehre, München: F. E.-C. Leuckart.
Meyer, Leonard B. (1956), Emotion and Meaning in Music, Chicago: University of Chicago Press.
Rameau, Jean-Philippe (1722), Traité de l’harmonie réduite à ses principes naturels, Paris 1722. Fotomech. Repr. in: Ders., »Complete theoretical writings«, ed. by Erwin R. Jacobi, Am. Inst. of Musicology, Vol I, 1967.
_____ (1726), Nouveau Système de musique théorique, Paris 1726. dto. Vol II, 1967.
Richter, Ernst Friedrich (171886), Lehrbuch der Harmonie, Leipzig: Breitkopf & Härtel.
Riemann, Hugo (101929), Handbuch der Harmonielehre, Leipzig: Breitkopf & Härtel.
Schönberg, Arnold (31922), Harmonielehre, Wien: Universal Edition.
Schenker, Heinrich (1956), Neue musikalische Theorien und Phantasien III: Der freie Satz, Neuausg. Wien: Universal Edition.
Sechter, Simon (1854), Die Grundsätze der musikalischen Komposition, Bd. 2, Leipzig: Breitkopf & Härtel.
Vogel, Martin (1962), Der Tristan-Akkord und die Krise der modernen Harmonielehre, Düsseldorf: Gesellschaft zur Förderung der systematischen Musikwissenschaft e. V.
Weber, Gottfried (1821), Versuch einer geordneten Theorie der Tonsetzkunst, Bd. 3, Mainz: Schott.
Wittgenstein, Ludwig (1969), »Philosophische Untersuchungen«, in: Ders., Schriften 1, Frankfurt a. M.: Suhrkamp, 279–544.
Dieser Text erscheint im Open Access und ist lizenziert unter einer Creative Commons Namensnennung 4.0 International Lizenz.
This is an open access article licensed under a Creative Commons Attribution 4.0 International License.




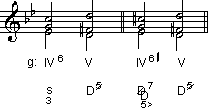






 «; dieser erscheint zuerst bei Ernst Friedrich Richter (1886, 42), später auch bei Salomon Jadassohn (1895, 54), jedoch zunächst nicht in Kombination mit dem Stufensymbol, sondern separat über dem Liniensystem des Basses. Zur Geschichte der musiktheoretischen Deutung des Quartsextakkords von Rameau bis Schenker vgl. Beach 1967.
«; dieser erscheint zuerst bei Ernst Friedrich Richter (1886, 42), später auch bei Salomon Jadassohn (1895, 54), jedoch zunächst nicht in Kombination mit dem Stufensymbol, sondern separat über dem Liniensystem des Basses. Zur Geschichte der musiktheoretischen Deutung des Quartsextakkords von Rameau bis Schenker vgl. Beach 1967.