Der Begriff der ›Überleitung‹ und die Musik Mozarts

Zum Begriff

Sowohl der deutschen als auch der nordamerikanischen Literatur lässt sich ein deutliches Unbehagen am Begriff der ›Überleitung‹ bzw. seines amerikanischen Pendants ›Transition‹ entnehmen:

Einerseits wächst darum aus dem Hauptthema eine Strecke heraus, die zum Seitenthema leitet; sie wird gewöhnlich (jedoch meist sachlich zu unrecht) als modulierende ›Überleitung‹ bezeichnet.[2]

The standard designation for this music, transition (or bridge), is problematic, at times misleading. It can be particularly deceptive within analytical contexts that assume as a first principle that tonal considerations trump all others, thus suggesting that the term means a transition or bridge from one key to another.[3]

Dieses Unbehagen dürfte Ausdruck eines Skrupels in der musikwissenschaftlichen Forschung sein, deren Bemühungen dahin gehen, ein Phänomen möglichst in der Gesamtheit der historischen Bezüge darzustellen und hierfür Begriffe zu wählen, welche die spezifischen Eigenheiten der Phänomene nicht verunklaren. Nur in diesem Sinne lassen sich die Ausdrücke »sachlich zu unrecht« und »at times misleading« rechtfertigen, weil die Gefahr besteht, dass eine historisch spätere Sicht auf ein zeitlich früheres Ereignis unkritisch übertragen bzw. der ›eigene Geist‹ für den ›Geist der Zeiten‹ ausgegeben wird. In der systematischen Forschung ergibt sich dagegen nicht selten das Problem der Benennung von Phänomenen, für die noch keine Bezeichnung existiert. In diesem Fall leisten unsinnige Bezeichner allerdings die gleiche Funktion wie semantisch passende, da auch diese grundsätzlich ein Identifizieren und Ansprechen von Gegenständen ermöglichen. In der vorliegenden systematischen Untersuchung wird der Terminus ›Überleitung‹ als Bezeichner für einen spezifischen Abschnitt in der Musik Mozarts verwendet, die folgenden Ausführungen erörtern die Beschaffenheit von Überleitungen.

Zum Vorhaben

In der Musiktheorie besteht ein grundsätzliches Dilemma zwischen Abstraktion und Konkretisierung. Sind Beschreibungen zu abstrakt, steht Musiktheorie in der Kritik, sie entferne sich zu sehr von der ›lebendigen Musik‹, und mit dem Zeigefinger auf der Diskrepanz zwischen musikalischem Gegenstand und seiner Beschreibung schlägt die Stunde des musikwissenschaftlichen Hermeneutikers, der musiktheoretische Systematik in eine ›theoretische Interpretationsgeschichte‹ aufzulösen gewohnt ist. Aufgelöst werden damit jedoch nicht nur die Unzulänglichkeiten, sondern auch die Möglichkeiten systematischer Erkenntnis. Sind musiktheoretische Beschreibungen hingegen zu konkret, lässt sich daran zwar die Hoffnung knüpfen, die Individualität des Gegenstandes eingefangen zu haben, doch bleibt man damit auch gefangen unter jenem Abstraktionsniveau, von dem aus intertextuelle und stilanalytische Forschungen sinnvoll möglich wären.

Niklas Luhmann hat unter dem Stichwort »Distanzierung der Vergleichsgesichtspunkte« ein Ziel wissenschaftlichen Arbeitens formuliert:

Theoriearbeit im Sinne einer Verwissenschaftlichung von Aussagen bemüht sich mithin auf einem Kontinuum des Vergleichsinteresses um zunehmend unwahrscheinliche Vergleiche, also um Feststellungen von Gleichheiten an etwas, was zunächst als ungleich erscheint. Es geht um Distanzierung der Vergleichsgesichtspunkte und damit nicht zuletzt um eine Erweiterung des Bereichs praktischer Substitutionsmöglichkeiten. Flugzeuge müssen nicht, wenn man einmal die Flugphysik beherrscht, als Copie von Vögeln gebaut werden.[4]

So unterschiedlich wie Vogel und Flugzeug wirken auch die beiden nachstehenden Überleitungen von Wolfgang Amadeus Mozart und Ludwig van Beethoven. Niemand wird ernsthaft in Zweifel ziehen wollen, dass hier äußerst Ungleiches erklingt:

Abb. 1: W.A. Mozart, Überleitung des 1. Satzes der Sonate in C-Dur KV 14, T. 11–14 (oben) und L. v. Beethoven, Klaviersonate in F-Dur op. 10, Nr. 2, 1. Satz, T. 13–37 (unten)

Im Sinne einer »Distanzierung der Vergleichsgesichtspunkte« wird in diesem Beitrag dargelegt, dass sich diese beiden Überleitungen als Instanzen des gleichen Idealtyps[5] bzw. Überleitungsmodells verstehen lassen. Der Nachweis ist dabei nicht Selbstzweck, er erfolgt vor dem Hintergrund zahlreicher Analysen, unter Berücksichtigung zeitgenössischer Quellen und im Hinblick auf ein spezifisches Forschungsinteresse. Ziel ist es, belastbare Überleitungsmodelle zu definieren sowie einen Theorieaufbau zum Thema ›Überleitung‹ in der Musik Mozarts zu initiieren.[6]

Ein Idealtyp

Als Überleitung wird vorerst eine Taktgruppe mit der Formfunktion bezeichnet, den Beginn einer Komposition – bzw. eine erste Taktgruppe in der Ausgangstonart – mit spezifischen Gestaltungen in der Nebentonart zu verbinden. Die Idee für einen satztechnischen Idealtyp gaben dabei Überleitungen, die Mozart anhand des Nannerl-Notenbuchs geübt und in seinen frühesten Kompositionsversuchen verwendet hat. Das erste Beispiel zeigt die Überleitung des Allegros in C-Dur aus dem Nannerl-Notenbuch (zum besseren Vergleich nach B-Dur transponiert), daneben die Überleitung aus dem am 4. März 1762 entstandenen Allegro in B-Dur KV 3, die sich wie eine unverzierte Fassung der Takte des Notenbuch-Allegros ausnimmt.

Abb. 2: a) Nannerl-Notenbuch Nr. 40, Allegro in C-Dur, T. 7–10, transponiert, b) KV 3, T. 7–8 und c) dreistimmiger Gerüstsatz

Der unter c) abgebildete Gerüstsatz entspricht einem Beispiel, das Wolfgang Amadeus Mozart selbst in ein Unterrichtsheft notiert hat (Abb. 3 oben rechts). Im Wesentlichen findet sich die Wendung auch in dreistimmigen Tonleiterharmonisierungen einer bei Lotter gedruckten Generalbassanleitung von Johann Xaver Nauß aus dem Jahre 1751 (Abb. 3 oben links). Leopold Mozart dürfte diese Anleitung gekannt haben, da er in Salzburg als Kommissionär des Verlagshauses fungierte. Ein weiteres Beispiel für diese Form der ›Regola dell’ottava‹ lässt sich einer Unterrichtsabschrift entnehmen, welche nach Bernd Kohlschütter »wohl unbedenklich, vor allem nach den in Salzburg vorhandenen Versetten und Kadenzen Johann Ernst Eberlin zugesprochen werden«[7] kann (Abb. 3 unten). Diese Anleitung darf somit als Zeugnis der Salzburger Musikausbildung um 1760 gelten:

Abb. 3: Oben links: Nauß, Johann Xaver (1751), Gründlicher Unterricht den General-Baß recht zu lernen […], Augsburg: Johann Jacob Lotters seel. Erben, S. 26.; oben rechts: W.A. Mozart, KV 453b (Ployer-Studien), Blatt 3b und unten: Handschrift Fundamentum del Eberlin Mbs Ms. Mus. 261 (1760)

Sowohl bei Nauß als auch bei Mozart sind oberes sowie unteres Tetrachord der jeweiligen Tonleitern auf gleiche Weise beziffert worden. Dem entspricht die motivische Gestaltung in der Unterrichtsabschrift »del Eberlin«, denn auch hier erklingen unabhängig von der übergeordneten Tonart immer wieder gleiche Oberstimmengestaltungen für gleiche Tetrachordharmonisierungen. Ohne bereits an dieser Stelle auf die harmonischen Besonderheiten der Handschrift einzugehen (Sekundakkord- und II-V-I-Harmonisierung), lassen sich die gezeigten Beispiele unter Vernachlässigung der Generalvorzeichnung wie folgt beschreiben: Im Bass erklingt zuerst ein Tetrachord 4-3-2-1 mit der Struktur Ht-Gt-Gt[8] (= fa-mi-re-ut)[9] sowie anschließend die Unterquinttransposition dieser Viertonfolge (also im Generalbassbeispiel links oben: g-fis-e-d und c-h-a-g, bei Mozart und im Diminutionsbeispiel: c-h-a-g und f-e-d-c).

Es wird behauptet:

1. Die Harmonik spezifischer Überleitungen in Dur-Kompositionen Mozarts wird reguliert durch die Möglichkeiten der im Hinblick auf die Musiksprache des 18. Jahrhunderts sinnvollen Harmonisierung der Töne eines Tetrachords (Ht-Gt-Gt bzw. fa-mi-re-ut).

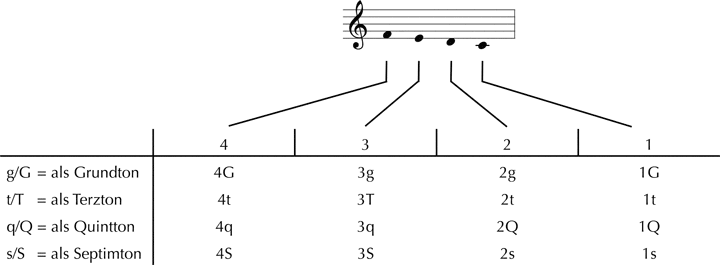
Die Beschränkung auf die Tetrachordstruktur fa-mi-re-ut ist vorläufig. Die Töne bilden metaphorisch gesprochen das Rückgrat einer Überleitungs-Harmonik, das einerseits die Anzahl möglicher Harmonieverbindungen einschränkt, zugleich aber ›harmonische und melodische Variation‹ (Portmann)[10] erlaubt. Im Sinne einer Harmonik des 18. Jahrhunderts können die Töne des Tetrachords vorerst als Grund-, Terz-, Quint- und Septimton harmonisiert werden. Welche Harmonisierung vorliegt, wird im Folgenden durch Buchstaben kenntlich gemacht, wobei ›G‹ für die Harmonisierung eines Tetrachordtons als Grundton, ›T‹ für eine Harmonisierung als Terzton, ›Q‹ als Quintton und ›S‹ als Septimton steht. Darüber hinaus sei vereinbart, dass große Buchstaben eine große Terz und kleine eine kleine Terz über dem Grundton kennzeichnen. Im Falle des in der Abb. 4 gezeigten Tetrachords stände ›4G‹ demnach für eine Harmonisierung des vierten Tons f als F-Dur (›f‹ als Grundton), ›4t‹ chiffriert dagegen einen d-Moll-Akkord (›f‹ als Terzton). ›2Q‹ kennzeichnet den zweiten Ton d des Tetrachords, der als Quinte eines G-Dur-Dreiklangs oder -Septakkords einen entsprechenden Klang in einer Komposition referenziert. Die folgende Abbildung zeigt die Kürzel in Tabellenform:

Abb. 4: Harmonisierungsmöglichkeiten

Für die Außenstimmensätze soll gelten, dass sie an den jeweiligen Harmoniefolgen partizipieren, darüber hinaus aber nicht festgelegt sind. Die vier häufig anzutreffenden Außenstimmensätze der Abb. 5 z.B. repräsentieren den gleichen Idealtyp 4G-3T-2Q-1G, die schwarzen Noten ohne Hals veranschaulichen den Tonleiterausschnitt 4–1 (fa-mi-re-ut):

Abb. 5: Mögliche Außenstimmensätze für 4G-3T-2Q-1G (Auswahl)

Der Außenstimmensatz (Terzparallelen) der Abb. 5a), bei dem Bassstimmenstruktur und Idealtyp kongruieren, charakterisiert die Überleitungen aus dem Allegro des Nannerl-Notenbuchs sowie aus KV 3 (s. Abb. 2b). Dieser Außenstimmensatz unterscheidet sich lediglich in der dritten Bassnote von der in der Abb. 5b) gezeigten Stimmführung. Die quantitativ kleine – für den jungen Mozart äußerst charakteristische – Veränderung muss qualitativ als bedeutsam bewertet werden, weil sie dem Grundton bzw. Abschluss der Harmoniefolge ein größeres Gewicht verleiht. In Abb. 5c) weist die strukturelle Oberstimme die gleiche Terzkoppelung zum idealtypischen Tetrachord auf wie in den vorangegangenen Beispielen, während der Bass selbständig agiert (Ausprägung ›grundstellige Akkorde‹). Und in Abb. 5d) schließlich haben sich sowohl Ober- als auch Unterstimme vom Verlauf des Idealtyps gelöst.

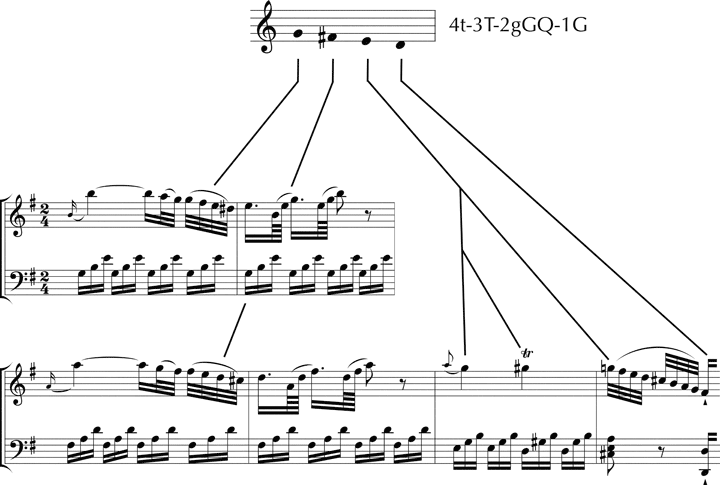
Des weiteren ist es möglich, dass ein Skalenton des Idealtyps durch zwei oder mehrere Harmonien ausgedrückt wird. Ein Beginn mit 4tS besagt, dass der vierte Ton eines Tetrachords zunächst als Terz- und in unmittelbarer Folge als Septimton erklingt, also für das Tetrachord f-e-d-c eine Harmonisierung des f als d-Moll- und G-Dur-Septakkord. In der Überleitung der Sonate in G-Dur KV 27 wird der zweite Ton e des Tetrachords sogar durch drei Harmonien (e-Moll, E-Dur- und A-Dur-Septakkord) repräsentiert:

Abb. 6: Tetrachord g-fis-e-d mit 4t-3T-2gGQ-1G im Kopfsatz der Violinsonate in G-Dur KV 27, T. 7–12 (o. Vl.)

Im frühen Werk Mozarts gibt es Überleitungen, die sich über die Möglichkeiten des Tetrachord-Idealtyps vollständig beschreiben lassen. Hierzu zählen zum Beispiel die Überleitungen aus KV 6/II, KV 6/IV, KV 7/II, KV 9/I, KV 9/II, KV 13/1, KV 27/I sowie KV 38/IV. In diesem Fall sind die Referenzen des Idealtyps mit dem Formteil Überleitung identisch.

Es wird behauptet:

2. Einige Überleitungen in Dur-Kompositionen Mozarts lassen sich vollständig mit Hilfe des Idealtyps ›Tetrachord‹ (fa-mi-re-ut) beschreiben.

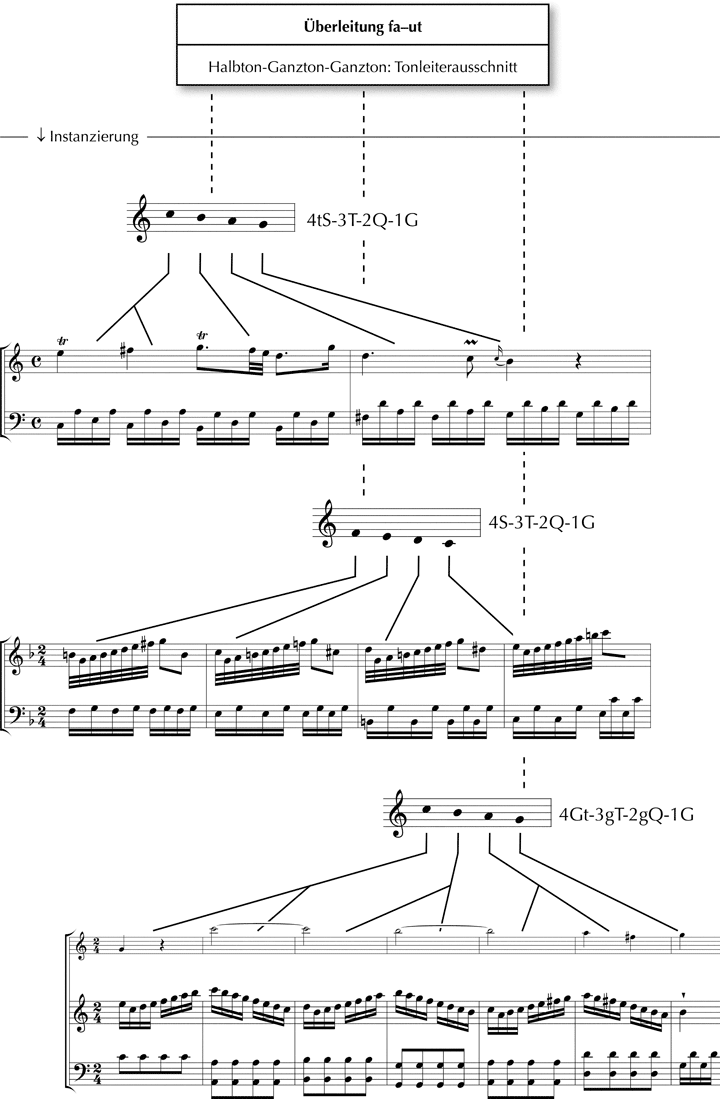
Referenzen dieses Idealtyps sollen ›Überleitung fa–ut‹ heißen. Das folgende Diagramm veranschaulicht exemplarisch die Überleitungen der Exposition des ersten und vierten Satzes der Sonate in C-Dur KV 6 (Instanzen C-G mit 4t-4S-3T-2Q-1G und 4G-4t-3g-3T-2g-2Q-1G) sowie die Überleitung aus der Exposition des ersten Satzes der Sonate in KV 13 (Instanz f–c mit 4S-3T-2Q-1G).

Abb. 7: Instanzen der ›Überleitung fa–ut‹ in verschiedenen Ausprägungen und tonalen Kontexten: KV 6/I (oben), KV 13/I (Mitte) und KV 6/IV (unten). Die ersten beiden Beispiele wurden aus pragmatischen Gründen ohne Violinstimme (= o. Vl.) abgebildet.

Wiederholung und ›bidirektionale‹ Fortschreitung

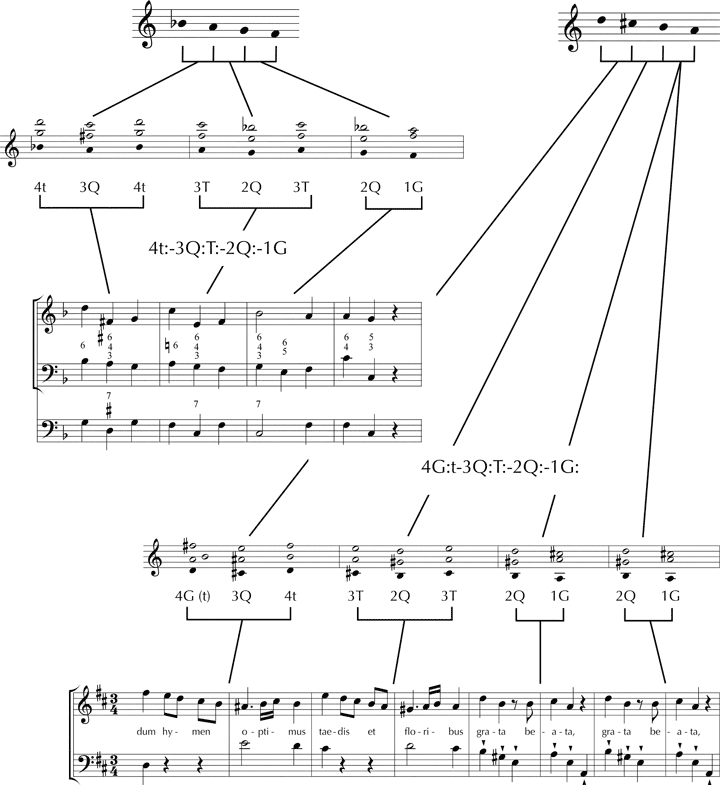
Es sei vereinbart, dass im Rahmen eines idealtypischen Tetrachords Aufwärtsbewegungen, denen eine erneute Abwärtsbewegung folgt, nicht zur Annahme eines neuen Überleitungsmodells führen. Die Möglichkeiten solcher Fortschreitungen, die im Folgenden als ›bidirektional‹ bezeichnet werden, hat Mozart unterrichtet und komponiert. Ein Generalbassbeispiel in Mozarts Handschrift aus dem Unterrichtsheft KV 453b sowie die Überleitung der Arie Nr. 4 aus dem lateinischen Intermedium Apollo und Hyacinth KV 38 lassen sich als Instanzen der ›Überleitung fa–ut‹ mit bidirektionaler Fortschreitung verstehen. Im Gegensatz zu Harmonien, die in unmittelbarer Folge erklingen und deren Symbole direkt hintereinander geschrieben werden (z.B. 4tS), kennzeichnet der Doppelpunkt (›:‹), wenn an einem Skalenton verschiedene Harmonien in Verbindung mit bidirektionaler Fortschreitung auftreten oder eine Harmonie im Zuge bidirektionaler Fortschreitung wiederholt vorkommt. Im Generalbassbeispiel der Abb. 8 zeigt beispielsweise der erste Doppelpunkt der Chiffre 3Q:T: an, dass die Harmonien D-Dur und F-Dur am dritten Ton a des Tetrachords b–f nicht unmittelbar hintereinander, sondern in getrennten Verbindungen erklingen: D-Dur (3Q) bildet einen Zusammenhang mit g-Moll (4t) und C-Dur (2Q) mit F-Dur (3T). Der zweite Doppelpunkt steht für das wiederholte Auftreten des dritten Skalentons mit einer Harmonisierung als Terz (3T):

Abb. 8: Instanzen der ›Überleitung fa–ut‹ mit bidirektionaler Fortschreitung im Unterrichtsheft KV 453b in der Handschrift Mozarts und in der Arie Nr. 4 des lateinischen Intermediums Apollo und Hyacinth KV 38 (nur Gesang und Bass)

Zu dem Beispiel aus der Arie sei noch erwähnt, dass der Beginn harmonisch ambivalent ist, da auch in der Orchesterbegleitung nur eine zweistimmige Terz d-fis erklingt, was sowohl D-Dur als auch h-Moll als Interpretation zulässt.

Ein Sonderfall bidirektionaler Fortschreitung sind Rücksprung und Wiederholung. Wie bereits erwähnt, werden im Kopfsatz der Überleitung aus KV 6 die in der Abb. 7 (oben) wiedergegebenen Takte als Ganzes wiederholt. Es entspricht analytischen Konventionen, eine solche Wiederholung nicht als neues Modell zu klassifizieren. Die Chiffrierung dieser Überleitung lautet daher 4tS:-3T:-2Q:-1G:

Auch die in der Abb. 7 (Mitte) wiedergegebene Überleitung aus KV 13 muss im Hinblick auf die Möglichkeit bidirektionaler Erklärung für unvollständig erklärt werden, da sich der dem abgebildeten Beispiel folgende Verlauf (T. 21–33) als mehrfache Wiederholung des Tetrachords (f–c) mit differenten harmonischen Ausarbeitungen verstehen lässt. Die Überleitung aus KV 13 (T. 11–33) wäre unter Berücksichtigung der bidirektionalen Fortschreitung als 4S:G:-3T:Q-2Q:gQ:-1G: (= 4S-3T-2Q-1G-4G-3T-2g-2Q-1G-4G-3T-2g-2Q-1G-2Q-1G-4G-3Q-2g-2Q-1G) zu chiffrieren. Diese überproportional lange Überleitung ist im Zusammenhang mit den kompositorischen Versuchen des jungen Mozart zu sehen, spezifische Formfunktionen (wie Überleitung und Schlussgruppe) durch Erweiterungen zu dehnen.[11]

Der Quintabsatz

Auch vor dem Hintergrund möglicher Wiederholungen und bidirektionaler Fortschreitungen lassen sich Überleitungen in der Regel nicht vollständig über den bisher erörterten Idealtyp beschreiben. Für Mozart z.B. sind Überleitungen ohne einen kadenziellen Abschluss nur in sehr frühen Kompositionen charakteristisch (viele solcher Überleitungen entstammen Werken aus der Zeit zwischen 1762–1764). Sehr viel häufiger begegnet die Kombination einer idealtypischen Harmoniefolge mit einem ›Quintabsatz‹.[12]

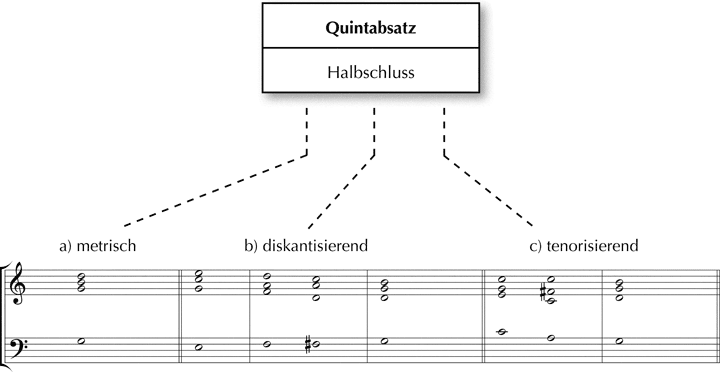
Quintabsätze lassen sich in der Regel als Halbschluss beschreiben, der a) über einen einzelnen dominantischen Akkord, b) eine diskantisierende oder c) eine tenorisierende Wendung im Bass realisiert werden kann:

Abb. 9: Der Quintabsatz als Halbschluss

Für Halbschlusswendungen werden im Folgenden die Kürzel Hs-m (= Halbschluss metrisch), Hs-d (= Halbschluss mit diskantisierender Bassstimme) und Hs-t (= Halbschluss mit tenorisierender Bassstimme) verwendet.[13] Das Generalbassbeispiel der Abb. 8 sowie das folgende Beispiel zeigen jeweils eine idealtypische Harmoniefolge, der sich unmittelbar eine metrisch schwer platzierte Dominante (Hs-m) anschließt. Beide Ereignisse zusammen bilden die Überleitung:

Abb. 10: Instanz der ›Überleitung fa–ut mit Halbschluss‹ im Kopfsatz der Sonate in C-Dur KV 14, T. 11–14

Es wird behauptet:

3. Ein Großteil der Überleitungen in Dur-Kompositionen Mozarts lässt sich als Kombination aus ›Tetrachord‹ (fa–ut) und Halbschluss verstehen.

Diese Überleitungen werden im Folgenden als ›Überleitung fa–ut mit Halbschluss‹ bezeichnet. Die nächste Abbildung zeigt zwei Instanzen dieser Überleitung mit gleicher harmonischer Prägung (4G-3T-2Q-1G) und gleicher Form des Halbschlusses (diskantisierend). Strukturell unterschieden sind die Beispiele dagegen in Hinblick auf den Fortschreitungsmodus (linear/bidirektional):

Abb. 11: Instanzen der ›Überleitung fa–ut mit Halbschluss‹ der Sonaten in B-Dur KV 10, 1. Satz, T. 9–14 (oben) und KV 189f (281) 1. Satz, T. 9–16 (unten)

Der linearen Fortschreitung in KV 10 zwischen den ersten beiden Positionen (B-Dur / F-Dur) steht ein bidirektionales Pendeln in KV 189f (281) gegenüber (Es-Dur / B-Dur / Es-Dur / B-Dur). In beiden Beispielen schließen sich den Tetrachord-Progressionen diskantisierende Halbschlusswendungen an, die sich im Sinne der paradigmatischen Gliederung Heinrich Christoph Kochs als dritter und zweiter Absatz klassifizieren lassen (Quintabsätze bzw. Halbschlüsse in der Quint- und Grundtonart). Für diese Untersuchung vernachlässigen wir jedoch die bei Koch artikulierte Ansicht, dass im Falle des dritten Absatzes »die Modulation nach der Tonart der Quinte hingeleitet«[14] wird, und betrachten vorerst beide Beispiele der Abbildung 11 als Instanzen des gleichen Überleitungsmodells auf verschiedenen Tonstufen.

›Variation‹

Im Folgenden werden die ›harmonische Variation‹ (Portman) bzw. die im 18. Jahrhundert gebräuchlichen Instanzen der ›Überleitung fa–ut mit Kadenz‹ erörtert. Die harmonischen Möglichkeiten der Skalentöne 4–1 werden hierzu im Einzelnen besprochen und durch Beispiele dokumentiert.

Der vierte Skalenton (4)

Der Beginn von Überleitungen mit einem Durdreiklang über dem vierten Skalenton 4G ist für Mozart ein Standard, Beispiele hierfür geben die Abbildungen 2, 7, 8, 10 und 11 bzw. die Überleitungen der Kompositionen KV 3, KV 6/IV, KV 10/I, KV 14/I, KV 38/IV und KV 189f/I (281).

Für eine mit einem Mollakkord beginnende Überleitung (4t) sind bereits exemplarisch KV 27/I und KV 6/I genannt worden (vgl. hierzu die Abbildungen 6 und 7), typisch für das Auftreten dieser Harmonisierungsvariante im Frühwerk Mozarts ist der Sextakkord, dem in der Regel ein weiterer Sextakkord an der Position des dritten Skalentons folgt.[15]

Im Februar 1778 komponierte Mozart in Mannheim in der Violinsonate KV 293b (302) eine entsprechende Überleitung noch mit konventionellem Beginn 4Gt-3Q-2gQ-1g (mit 4t als Sextakkord). Hier allerdings korrespondiert bereits ein chromatisierter tenorisierender Halbschluss (›phrygische Wendung‹) mit dem Molldreiklang beim ersten Skalenton (1g):

Abb. 12: ›Überleitung fa–ut mit Halbschluss‹ im Kopfsatz der Violinsonate in Es-Dur KV 293b (302), T. 33–40

Verminderte und halbverminderte Septklänge mit dominantischer Funktion im Sinne der Funktionstheorie, im Beispiel oben also z.B. die Klänge an den Positionen des dritten und zweiten Skalentons, werden im Sinne ›verkürzter Dominantseptnonakkorde‹ chiffriert. Halbverminderte Septakkorde oder verminderte Dreiklänge ohne dominantische Funktion im Sinne der Funktionstheorie, z.B. im Rahmen einer Quintfallsequenz, werden dagegen nicht auf substruierte Fundamente bezogen. Diese Entscheidung hat systematische und pragmatische Gründe: Zum einen ist nur auf diese Weise eine eindeutige Chiffrierung ohne Zuhilfenahme weiterer Buchstaben für Dur- und Mollklänge sowie für verminderte und übermäßige Akkorde gegeben, zum anderen ist eine einheitliche Kennzeichnung für dominantische Funktionen wünschenswert. Darüber hinaus steht diese Kennzeichnung im Einklang mit der Funktionstheorie in der Nachfolge Riemanns, die in Deutschland weit verbreitet ist. Die Fragen, ob eine solche Bezeichnung auch ›historisch korrekt‹ ist bzw. ob Mozart auf diese Weise gedacht hat, ob darüber hinaus Fundamente lediglich Denkhilfen darstellen oder ob sie für real erklingende Phänomene stehen etc., sind für diese Untersuchung nicht von Bedeutung.

Nach seiner zweiten Frankreichreise tendiert Mozart bei den mit einem Mollklang beginnenden Überleitungen zu manieristischen Ausarbeitungen, die in ihrem Charakter an ›Theaterdonner‹ erinnern. Als Drohung in d-Moll (Einstein), gespensterartig aus dem Dunkel hervorschießend (Abert) und als chromatisches Abenteuer (Kühn) hat z.B. die Ausarbeitung im Kopfsatz der Klaviersonate in F-Dur KV 300k (332) Musikwissenschaftler und Musiktheoretiker des 20. Jahrhunderts gleichermaßen verzückt.[16] Sie findet sich in verwandter Form neben anderen Werken auch im Kopfsatz der Violinsonate in Es-Dur KV 481:

Abb. 13: Emphatischer Moll-Beginn durch Instanzen der ›Überleitung fa–ut mit Halbschluss‹ in den Sonaten in F-Dur KV 300k (332), 1. Satz, T. 22–40 (oben) und KV 481, 1. Satz, T. 24–36 (unten)

Der vierte Skalenton als Quinte (4q) ist in der Regel Bestandteil eines verminderten Dreiklangs. Ohne dominatische Funktion im Sinne der Funktionstheorie wird er als eigenständiger Akkord (s. Abb. 14), andernfalls als Vertreter eines Dominantseptakkords bezeichnet. Instanzen einer dominantisch beginnenden Überleitung (4S) finden sich in den gegebenen Exempla im Kopfsatz der Sonate in F-Dur KV 13, T. 17–20 (Abb. 7 mittleres Beispiel) sowie im langsamen Satz der Sonate in C-Dur KV 6, T. 8–11.

Der dritte Skalenton (3)

Die Variante eines grundstelligen Dreiklangs (3g) über dem dritten Skalenton findet sich bei Mozart im Rahmen von Sequenzen. Sie ist hier zum einen Bestandteil eines stufenweise abwärts sequenzierten Terzfalls, eines älteren Sequenzmodells, für das sich im musikanalytischen Diskurs bisher kein griffiger Name durchgesetzt hat, zum anderen Teil einer Quintfallsequenz. Für den erstgenannten Fall wurde bereits mit dem letzten Satz der Sonate in C-Dur KV 6 ein Beispiel gegeben (Abb. 7 unten), als weitere Referenz wäre die Überleitung des Schlusssatzes der Violinsonate in B-Dur KV 454 (T. 47–48) zu nennen. Eine Quintfallsequenz findet sich in Verbindung mit einem tenorisierenden Halbschluss in dem ersten überlieferten Autograph Mozarts, dem Sonatensatz in C-Dur KV 5a (9a):[17]

Abb. 14: Instanz der ›Überleitung fa–ut mit Halbschluss‹ mit einem grundstelligen Dreiklang am dritten Skalenton (Quintfallsequenz) im Sonatensatz in C-Dur KV 5a (9a), T. 9–14

Im Schlusssatz der Violinsonate KV 274d (376) tritt der dritte Skalenton als Grundton eines halbverminderter Septakkords (3g) auf, dem ein Dominantseptakkord folgt:

Abb. 15: Instanz der ›Überleitung fa–ut mit Halbschluss‹ mit halbvermindertem Septakkord und Dominante am dritten Skalenton im Zuge einer kadenziellen Ausformulierung des zweiten Skalentons im Schlusssatz der Violinsonate in F-Dur KV 274d (376), T. 36–44

Interessant ist an diesem Beispiel die Inszenierungsweise, die in einer Reihe mit den ›Theaterdonner‹-Überleitungen aus KV 300k/I (332) sowie KV 481/I gesehen werden kann: Der grundstellige Mollbeginn mit dominantischer Hinführung, der motivische Parallelismus (ab-ab), das Dynamikmodell ›f-p-f-p‹[18], die Asymmetrie der Skalentondauern, die kadenzielle Festigung des zweiten Skalentons (3gQ-2g anstelle von 3gq-2g in der Quintfallsequenz des C-Dur-Allegro) und nicht zuletzt die Korrespondenz der kadenziellen Abschlüsse – also einer Syntax, die man mit ›Festgefügtem‹ (4+4) assoziieren möchte und die auf Beethovens Ausarbeitung in op. 10, Nr. 3 vorverweist – sind Merkmale einer kunstvollen Überformung traditioneller Gestaltungen.

Die Harmonisierung des dritten Skalentons als große Terz eines Dreiklangs (3T) gehört zum Standard mozartscher Überleitungen und ist in Verbindung mit allen besprochenen Möglichkeiten des vierten Skalentons (4G, 4t und 4S) üblich. Beispiele hierfür finden sich u.a. in den Abbildungen 1, 6 und 7 (mittleres Beispiel).

Die harmonische Prägung des dritten Skalentons als Quinte eines Dur-Dreiklangs (3Q) ist typisch im Kontext eines Moll-Beginns der Durchführung (4t-3Q, vgl. hierzu das Beispiel der Abb. 12). Die Weiterführung 3Q-2gQ-1G wie in den Kopfsätzen KV 293b (302), KV 300k (332), KV 481 oder auch im Schlusssatz von KV 274d (376) ergibt dabei jene VI#-II-V-I-Sequenz[19], die Joseph Riepel als ›Fonte‹ bezeichnet und zu deren Bedeutung für die Entwicklung der Sonatenform bei Mozart ich mich an anderer Stelle ausführlich geäußert habe.[20]

Die Harmonievariante des dritten Skalentons als Septime (3S) kann vorerst nur durch ein Beispiel belegt werden: Im ersten Satz der formal ungewöhnlichen Violinsonate in C-Dur KV 293c (303) wird nach der Darstellung des vierten Skalentons durch die Harmonien C-Dur, a-Moll und D-Dur (4GtS) der dritte Skalenton durch einen G-Dur- sowie großen C-Dur-Septakkord repräsentiert (3TS). Der Abschluss der Harmoniefolge entspricht dem Standard (2Q-1G), ihm schließt sich eine diskantisierende Halbschlusskadenz an:

Abb. 16: Dreiklang und Septakkord an der Position des dritten Skalentons im Kopfsatz der Violinsonate in C-Dur KV 293c (303), T. 10–18

Mit dieser Taktgruppe endet ein 18-taktiger Adagio-Abschnitt, der traditioneller Weise als langsame Einleitung zu dem sich anschließenden schnellen Satz (›Molto Allegro‹) verstanden werden könnte. Ein Erkennen der Instanz 4GtS-3TS-2Q-1G + Hs-d einer ›Überleitung fa–ut mit Halbschluss‹ ermöglicht jedoch ein anderes Formverständnis: Die dem Beispiel oben vorangehenden Takte 1–10 bilden den Hauptsatz, der mit einem Grundabsatz in der Ausgangstonart endet und dem sich die abgebildete Überleitung anschließt. Das nach der Generalpause einsetzende ›Molto Allegro‹ beginnt demnach an der Position des Seitensatzes. Hierfür spricht zum einen die nach der Generalpause einsetzende VI#-II-V-I-Harmonik (Fonte), die auch für diese formale Position als charakteristisch bezeichnet werden darf, vgl. hierzu z.B. das Duetto aus KV 35a (42) sowie die Seitensätze aus den Klaviersonaten in C-Dur KV 189d (279) und in B-Dur KV 315c (333) sowie den Violinsonaten in B-Dur KV 317d (378) und F-Dur KV 547. Zum anderen lässt sich der Formverlauf in den Folgetakten als Schlussmusik einer Exposition verstehen (T. 27–88). Die Finesse des Satzes liegt also darin, dass man weder den langsamen Beginn als Hauptsatz noch den Anfang des schnellen Teils als ›cantabeln Satz‹[21] erkennen kann, sondern ersteren als langsame Einleitung und letzteren als Hauptsatz zu interpretieren geneigt ist. Erst in der Stauchung des Molto Allegro erschließt sich im Nachhinein ein höchst kunstvoller Manierismus der Form.

Der zweite Skalenton (2)

Der zweite Skalenton als Grundton eines Molldreiklangs (2g) bildet in Verbindung mit der Quinttonharmonisierung (2Q) eine II-V-I-Wendung, die den ersten Skalenton als Grundton stabilisiert. Diese äußerst häufige Harmonisierung ist in verschiedenen Außenstimmensatzprägungen bei Mozart anzutreffen, Beispiele hierfür finden sich in den Abb. 6, 7, 12, 13, 14 und 15 bzw. in den Überleitungen der Sätze 6/IV, KV 5a (9a), KV 27/I, KV 293b/I (302), KV 300k/I (332), KV 274d/I (376) und KV 481/I.

Der zweite Skalenton als Terz (2t) ist in der Regel in der Diatonik der lokalen Tonart wiederum Bestandteil eines verminderten Dreiklangs und wird – wie bereits in Verbindung mit der Harmonievariante 4q – in den meisten Fällen als Vertreter eines dominantischen Septakkords (2Q) zu interpretieren sein. Eine Ausnahme findet sich im 4. Satz der Violinsonate in B-Dur KV 454 (T. 37–49), wo die Sequenzlogik (4Gt-3gt-2gt-1G) die Annahme eines verminderten Dreiklangs rechtfertigt.

Der zweite Skalenton als Quinte (2Q) darf als einfache Variante der bereits erwähnten II-V-I-Wendung 2gQ gelten, beide Möglichkeiten sind mit gleichem Außenstimmensatz anzutreffen:

Abb. 17: Harmonisierung des Eintritts des zweiten Skalentons als Terzquartakkord oder Molldreiklang

Obwohl man aus heutiger Sicht geneigt sein mag, den Bass der Abb. 17 als Träger einer II-V-I-Harmonieverbindung zu interpretieren, dürfte für Mozart a) ein dominantischer Terzquartakkord mindestens ebenso gebräuchlich gewesen sein wie b) die II-V-I-Variante mit verkürztem harmonischen Rhythmus.[22] Der Quintharmonisierung des zweiten Skalentons kommt in den hier erörterten Beispielen jedenfalls die Bedeutung einer ›conditio sine qua non‹ zu, sie findet sich als Vorschlussharmonie der Tonleiterstruktur in allen hier abgebildeten Kontexten.

Für den zweiten Skalenton als Septime eines Dominantseptakkords (2S) konnte im Rahmen von fa–ut-Überleitungen schneller Kopfsätze bisher kein Beispiel ermittelt werden.

Abschließend sei im Hinblick auf die Harmonisierung des zweiten Skalentons vereinbart, dass sich über 2g (zweiter Skalenton als Grundton eines Septakkords) auch phrygische Wendungen chiffrieren lassen. Im ersten Satz der Violinsonate KV 247f (380) z.B. werden die Harmonien c-Moll, es-Moll-Sextakkord und F-Dur-Dominantseptakkord als Repräsentation des zweiten Skalentons ›c‹ eines B-Dur Tetrachords (es-d-c-b) interpretiert:

Abb. 18: Violinsonate in Es-Dur KV 274f (380), erster Satz, T. 13–21

In Übereinstimmung mit der Generalbasspraxis der Zeit wird hierzu der es-Moll-Sextakkord als Fragment eines Terzquartakkordes aufgefasst bzw. die Wendung es-Moll/F-Dur als Ausprägung des Fundamentschritts c-f verstanden.

Exkurs: ›La petite Sixte‹

Äußerungen zur ›französischen Sexte‹ finden sich bei zahlreichen Autoren des 18. Jahrhunderts, z.B. schreibt Carl Philipp Emanuel Bach 1762 im Versuch über die wahre Art das Clavier zu spielen, dass es eine »Gelegenheit zur Verwirrung« gäbe, wenn statt der nötigen Terzquart-Bezifferung nur »eine blosse 6« über den Noten stände.[23] Unter den von Bach gegebenen Beispielen sind phrygische Halbschlusswendungen, die vergleichbar sind mit jener aus Mozarts Komposition KV 274f (380). Bachs Appell, eindeutige Generalbassziffern zu verwenden, bezieht sich auf eine ältere Praxis, den zweiten und sechsten Ton einer Tonleiter mit einer ›6‹ als Generalbassanweisung generell als Terzquartakkord zu spielen. Johann Mattheson schreibt in seiner kleinen Generalbassschule knapp drei Jahrzehnte früher:

Ferner, ist hier die Frage gar nicht, was ein geschickter und erfahrner Spieler im General-Baß für erlaubte Freiheiten zu nehmen, und damit seine Begleitung auszuschmücken wisse; da es freilich an dem ist, daß geübte Meister zwar bei dem gemeinsamen Accord der grossen Sext fast jederzeit, zum Zierrath, eine Quarte mitzugreiffen pflegen, wenn diese vorher schon in der Hand gewesen ist, und sich gleich hernach, bey dem folgenden Accord, in ein wohlklingendes Intervall verändert, welches die Franzosen, wie schon oben pag. 165 beyläuffig erwehnet worden, la petite Sixte nennen […].[24]

Ausführungen zur ›petite Sixte‹ finden sich auch in einer Augsburger Generalbassanleitung von Georg Joachim Joseph Hahn aus dem Jahre 1751:

Abb. 19: Auszug aus Hahn, 1751, 42

Im oberen Notenbeispiel aus Hahns Generabassanleitung ist eine phrygische Wendung auf den Ton h mit 7-6-Bezifferung über dem Ton c zu sehen, die ohne weitere Anweisung als Terzquartakkord ausgesetzt worden ist (›Sexta modi‹). In vergleichbarer Weise, wie auf dem vierten Viertel des drittletzten Taktes die ›6‹ (a-Moll-Sextakkord) als Terzquartakkord zu spielen ist, wird in der vorliegenden Untersuchung der es-Moll-Sextakkord als Terzquartakkord gelesen, wobei die hinzugedachte übermäßige Quarte c eine Zuordnung zum zweiten Skalenton des idealtypischen Tetrachords (es-d-c-b) gestattet.

Nach diesen kurzen Bemerkungen zur ›petite Sixte‹ wäre ein weiteres Problem hinsichtlich der Überleitung des ersten Satzes aus KV 274f (380) zu diskutieren: Die sich der Tetrachord-Harmoniefolge anschließende Bassstimme (es-e-f) beginnt zwar wie die eines diskantisierenden Halbschlusses, erweist sich jedoch als Beginn einer Aufwärtssequenz, die über eine Tonleiterbewegung in den Grundton der Nebentonart führt:[25]

Abb. 20: Violinsonate in Es-Dur KV 380, 1. Satz, T. 20–23 (oben) und Violinsonate in C-Dur KV 6, 1. Satz, T. 11–14

Die weitere Analyse des Satzes bereitet keine Probleme, wenn diese Sequenz als Teil der Überleitung gedeutet wird. Die Überleitung in KV 274f/I (380) wäre demnach nicht als Instanz der ›Überleitung fa–ut mit Halbschluss‹, sondern als Exemplar eines neuen Modells ›Überleitung fa–ut mit Sequenz‹ anzusehen. Auch im Kopfsatz der Sonate in C-Dur KV 6 folgt der Wiederholung der in der Abb. 7 gezeigten Taktgruppe eine Aufwärtssequenz (Abb. 20 unten), die sich weder als Seitensatz noch als Schlussgruppe auffassen lässt. Die Überleitungen beider Kopfsätze bilden somit Instanzen des Modells ›Überleitung fa–ut mit Sequenz‹.

Es wird behauptet:

4. Einige wenige Überleitungen in Dur-Kompositionen Mozarts erweisen sich als Kombination aus ›Tetrachord‹ (fa–ut) und Sequenz.

Diese Überleitungen werden im Folgenden ›Überleitung fa–ut mit Sequenz‹ genannt.

Der erste Skalenton (1)

Der Abschlusston des Tetrachords als Träger eines grundstelligen Dreiklangs (1G und 1g) findet sich in allen bisher genannten Beispielen, wobei der Mollabschluss häufig in Verbindung mit der Harmonisierung 4t-3Q-2gQ-1g – vgl. hierzu KV 300k/I (332) in der Abb. 13 oben – oder verwandten Ausarbeitungen anzutreffen ist. Die Technik des Einführens der globalen Nebentonart über die gleichnamige Molltonart wirkt dabei so charakteristisch, dass es naheliegend ist, von einem Ausdrucksmodell zu sprechen. Dessen Entwicklung in Überleitungen sowie Schlussmusiken von Expositionen zu untersuchen, ist hier nicht möglich und bleibt einer gesonderten Forschung vorbehalten.

Der erste Skalenton als Terz eines Molldreiklangs (1t) zeigt die Verzögerung der Auflösung in eine lokale Tonika durch einen Trugschluss, dem sich der Halbschluss vermittelt oder unvermittelt anschließen kann. Eine solche Überleitung hat Mozart z.B. im Schlusssatz der Klaviersonate KV 189d (279) gestaltet, die Verbindung der Glieder wird über einen Sextakkord bewerkstelligt:

Abb. 21: Der Eintritt des ersten Skalentons als Terz eines Trugschlusses (1t) in der Klaviersonate in C-Dur KV 189d (279), 1. Satz, T. 11–22

Es wurde bereits erwähnt, dass für den zweiten Skalenton als Septime eines Dominantseptakkords (2S) im Rahmen von fa–ut-Überleitungen schneller Kopfsätze bisher Referenzstellen fehlen. Nur im langsamen Satz der Sinfonie KV 319[26] ließ sich bisher eine solche Überleitung nachweisen, in der nach der Folge 2Q-1G die VI. Stufe der Nebentonart (1t) über eine Zwischendominante (2S) erreicht wird. Doch welche Gründe hätte Mozart in Fällen, die der abgebildeten Überleitung der Sonate KV 189d (279) strukturell ähnlich sind, haben können, den Schlussklang (1t bzw. im Beispiel oben e-Moll) nicht über die zugehörige Dominante zu erreichen (2S bzw. den e-Moll-Akkord über einen H-Dur-Septakkord)?[27] Eine weitergehende Erforschung des Korpus wird hier Klärung schaffen.

Die Quintharmonisierung des ersten Skalentons (1Q) im Rahmen einer Parallelismusharmonik findet sich in der interessanten Überleitung des Kopfsatzes in der Klaviersonate in B-Dur KV 570:

Abb. 22: Klaviersonate in B-Dur KV 570, 1. Satz, T. 20–40

Die Überleitung beginnt nach einer Kadenz in der Ausgangstonart mit zwei Akkordschlägen (g-Moll/D-Dur), wobei Dynamik (forte) und Harmonik (4t-3Q) an jene ›Theaterdonner‹-Inszenierung erinnern, die bereits die Kopfsätze der Klaviersonaten KV 300k (332) und KV 481 prägte (Abb. 13). Diesen Akkorden schließt sich unmittelbar eine Taktgruppe an (Pendelbewegung Es-Dur/B-Dur-Dominantseptakkord), die in ihrem lyrischen Ausdruck einen auffälligen Kontrast zum energischen Überleitungsbeginn bildet. Dabei verhindert die durch den Kontrast bewirkte Trennung die Wahrnehmung des stringenten harmonischen Zusammenhangs in den ersten vier Überleitungstakten (Parallelismus-Harmonik g-D-Es-B). Mit Hilfe des bidirektionalen Fortschreitungsmodus und unter der Vereinbarung, dass Chromatisierungen des idealtypischen Tonleiterausschnitts keine substantielle, sondern lediglich eine akzidentielle Veränderung bewirken[28], könnte die nun folgende Entwicklung als harmonische Variation bzw. Repräsentation der Skalentöne 3–2 in verschiedenen harmonischen Ausprägungen verstanden werden. In der Chiffrierung werden Chromatisierungen von Skalentönen durch ein ›b‹- oder ›#‹-Zeichen gekennzeichnet, das den entsprechenden Buchstaben (G|g|T|t|Q|q|S|s) voranzustellen ist. Die Chiffrierung 4t-3Q-2T-3bS-2T-3bS[…] ist dabei der Lesart 4t-3Q-2T-1Q-2T-1Q[…] ohne Chromatisierung vorgezogen worden, weil im erstgenannten Fall unter den dritten Skalenton jene Harmonien subsumiert werden können, welche die gleiche Position im Parallelismus repräsentieren (also ein D-Dur und B-Dur-Dominantseptakkord als Bindeglied zwischen g-Moll und Es-Dur bzw. als jeweils zweite Akkorde der Parallelismus-Sequenzen g/D/Es/B/c und g/B7/Es/G7/c).

Für die Bezeichnung der Überleitung aus KV 570 mussten zudem die Buchstaben ›N|n‹ neu hinzugenommen werden, die auf den ersten Blick befremdlich wirken könnten, weil sie ohne weitergehende historische Differenzierung die Existenz von eigenständigen Dominantseptnonakkorden in der Musik Mozarts suggerieren. Diese Bezeichnung ist Folge der Entscheidung, verminderte Septimenakkorde mit dominantischer Funktion im Sinne der Funktionstheorie als verkürzte Dominantseptnonenakkorde zu kennzeichnen. Der Zusatz ›N‹ ergibt sich somit zwangsläufig, wenn ein Skalenton als Septime eines verminderten oder halbverminderten Septakkords mit dominantischer Funktion auftritt. Die Tabelle zur Systematik (Abb. 4) wird daher um eine Zeile bzw. um die Kürzel 4n|3n|2N|1n erweitert. Für die Musik des 18. Jahrhunderts kann davon ausgegangen werden, dass Nonenakkorde nur mit großer Terz über dem Grundton bzw. mit dominantischer Funktion im Sinne der Funktionstheorie möglich sind. Um Missverständnissen vorzubeugen sei an dieser Stelle nochmals ausdrücklich erwähnt, dass die Art der Chiffrierung systematischen und pragmatischen Gesichtspunkten folgt, mit ihr verbindet sich keine Aussage zur Bedeutung bzw. Auffassung verminderter Septakkorde im 18. Jahrhundert.

Des Weiteren sei für die Überleitung des Kopfsatzes der Klaviersonate KV 570 hervorgehoben, dass der halbschlüssig wirkende C-Dur-Akkord ›bassierend‹ erreicht wird, ein Merkmal, das im Allgemeinen als sicheres Anzeichen für einen Ganzschluss gilt. Auch die bisher verwendete Systematik für Halbschlüsse (metrisch, diskantisierend, tenorisierend) wird daher um die Möglichkeit bassierender Halbschlüsse erweitert.

Nicht zuletzt ist es denkbar, die Quintharmonisierung des ersten Skalentons (1Q) über einen Trugschluss nach einem Dominantseptakkord zur VI. Stufe der Nebentonart herbeizuführen (d.h. im Falle eines Tetrachords b-a-g-f die Harmonisierung C⁷-F-A⁷-B). Dieser Harmoniefolge könnte sich ein diskantisierender Halbschluss G⁷-C anschließen, wobei die hier mögliche Bassstimme a-b-h-c sehr stringent wäre. Eine Referenz für eine Überleitung fehlt indes, eine Instanz d-cis-h-a mit 4S-3T-2S-1Q mit Ganzschluss bzw. in Akkorden: E⁷-A-Cis⁷-D […] H⁷-E-A) lässt sich am Ende der Exposition des Kopfsatzes der Klaviersonate in D-Dur KV 575 nachweisen (T. 47–50).

Exkurs: Beethoven

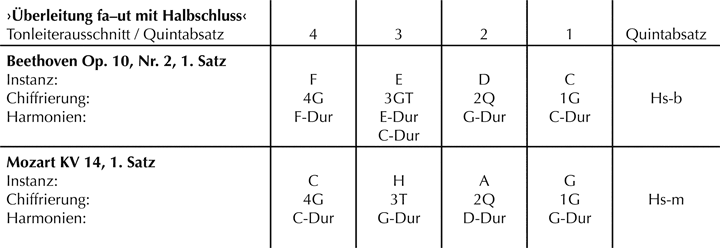
Die Überleitung im Kopfsatz der Sonate op. 10, Nr. 2 (Abb. 1) hat als charakteristisches Merkmal den dominantischen E-Dur-Orgelpunkt (T. 17–18), der vollkommen unerwartet nach dem Thema erklingt. Die Klangverbindung F-Dur/E-Dur ist grundsätzlich nicht ungewöhnlich, zumal sie über eine übermäßige Sexte (dis) vermittelt wird, die Formfunktion (›gleich nach dem Thema‹) dieses Quintabsatzes zur III. Stufe darf jedoch als einzigartig bezeichnet werden. Nach einer für Quintabsätze typischen Zäsur hebt die Musik mit einer prominenten Eröffnung[29] wieder an (T. 19–26) und führt über die Terzkette C-a-fis-D (T. 27–29) in einen dominantischen Orgelpunkt (T. 30ff.) in C-Dur bzw. den Quintabsatz der Nebentonart. Ohne die ästhetische Einzigartigkeit in Frage zu stellen, lässt sich die Überleitung im Kopfsatz aus op. 10, Nr. 2 im Sinne der hier vorgestellten Systematik beschreiben. Die Chiffrierungen dieser sowie der Überleitung aus Mozarts Violinsonate in C-Dur KV 14, die einleitend im Zuge einer »Distanzierung der Vergleichsgesichtspunkte« gegenübergestellt worden sind, zeigt die nachstehende Tabelle:

Abb. 23: »Distanzierung der Vergleichsgesichtspunkte« – Die Überleitungen der Kopfsätze der Klaviersonate in F-Dur op. 10, Nr. 2, 1. Satz, T. 13–37 und der Violinsonate in C-Dur KV 14, 1. Satz, T. 11–14

Beide Überleitungen erweisen sich als Instanzen des gleichen Modells (›Überleitung fa–ut mit Halbschluss‹), die Ausarbeitungen kongruieren harmonisch am vierten, zweiten und ersten Skalenton. Signifikant unterschieden sind hingegen die Ausarbeitungen am dritten Skalenton. An ihr findet sich in beiden Kompositionen ein Standardakkord (3T = Strukturton als Terz), Beethoven stellt diesem jedoch den bereits erwähnten grundstelligen E-Dur-Akkord (3G) mit dominantischer Wirkung voran. Das Besondere liegt nicht nur in dem überraschenden Eintritt des Quintabsatzes in a-Moll, sondern vor allem darin, dass die nachfolgende Standardharmonisierung des dritten Skalentons (3T bzw. C-Dur) durch die mediantische Einführung wie eine gänzlich neue und unverbrauchte Farbe wirkt. Die Harmonisierung des dritten Skalentons als Grundton von Klängen mit kleiner Terz über dem Grundton wurde in anderen Zusammenhängen bereits besprochen (Quintfallsequenz Abb. 14, Terzfallsequenz der Abb. 7 unten). Beethovens Ausarbeitung eines dominantischen Durakkords bzw. Quintabsatzes sowie der mediantischen Klangverbindung ist dagegen Zeugnis einer höchst kunstvollen und manieristischen Gestaltung.

Weiterhin sind die sich anschließenden Kadenzen verschieden: In KV 14 resultiert die Halbschlusswirkung aus einer metrisch schweren Dominante (Hs-m), bei Beethoven erklingt zur Vorbereitung der Dominante eine terzweise fallende Stufenfolge C-Dur, a-Moll, fis-vermindert und D-Dur, über den sich mit diminuiertem Quartsprung (d-g = bassierend) der dominantische Orgelpunkt zum Halbschluss in der Nebentonart anschließt.

Im Kopfsatz der Klaviersonate in D-Dur op. 10, Nr. 3 findet sich ein weiteres Zeugnis artifizieller Verfremdung, hier erklingt im Anschluss an den Hauptsatz eine liedhafte Periode in h-Moll mit einer förmlichen Ausweichung in die Tonart der Oberquinte:

Abb. 24: Ludwig van Beethoven, Klaviersonate in D-Dur op. 10, Nr. 3, 1. Satz, T. 17–30

Die ersten sechs Takte der Abb. 24 lassen sich als Beginn der Überleitung verstehen, sofern man gewillt ist, die Wiederholung des Themas mit geänderter Fortführung als Anzeichen für diesen Formteil zu akzeptieren.[30] Die Oktavenpassage sowie die nachfolgende Periode erweisen sich darüber hinaus als Instanz des Modells ›Überleitung fa–ut‹, das Einverständnis hinsichtlich der Bedeutung von Wiederholung und Chromatisierung des idealtypischen Tonleiterausschnitts weiterhin vorausgesetzt. Die Einzigartigkeit der Überleitung in op. 10, Nr. 3 ist demnach weder allein auf die Harmonik[31] noch die Syntax[32] gegründet, sondern resultiert aus dem Zusammentreffen der genannten Faktoren mit einem ausgesprochen lyrischen Ausdruck, der wie der Quintabsatz in op. 10, Nr. 2 allen Erwartungen an diese formale Position widerspricht.

Erweiterungen und Verkürzungen

Eine Erweiterung des idealtypischen Tonleiterausschnitts um einen Ton ist in Verbindung mit der Parallelismus-Harmonik anzutreffen. Im Kopfsatz der Violinsonate in D-Dur KV 300l (306) verbindet ein idealtypisches Pentachord die Ausgangstonart mit der Subdominante. Das Durchbrechen der Sequenzstruktur in der Bassstimme kündigt die Halbschlusswendung an, die Weiterführung der Sequenz in der rechten Hand gewährleistet eine nahtlose Verbindung zwischen idealtypischer Harmoniefolge und Halbschluss. Und um ein letztes Mal den Bogen zu Beethoven zu spannen: Eine weitere Instanz dieser Überleitung findet sich vor dem Seitensatz im Kopfsatz der 3. Sinfonie (›Eroica‹) op. 55. Das folgende Diagramm zeigt die Referenzen des Überleitungsmodells in beiden Kompositionen:

Abb. 25: W.A. Mozart, Violinsonate in D-Dur KV 300l (306), 1. Satz, T. 18–20 (o. Vl.) und Ludwig v. Beethoven, Sinfonie in Es-Dur op. 55, 1. Satz T. 37–45 (nur Streicher)

Zu diesen Beispielen seien zwei Beobachtungen angemerkt:

1.) Idealtypische Tonleiterausschnitte sind abstrakte Denkeinheiten, die auch für den Fall als Erklärungsmodus stimmig sein können, dass sie sich nicht real klingend vorstellen lassen. Dass die Beispiele der Abb. 25 Instanzen des gleichen Modells zeigen, dürfte musikalisch evident sein. Die Bezeichnung 4Q – also der vierte Skalenton d als Quinte eines G-Dur-Klangs – lässt sich allerdings nur bei Mozart in transponierter Form (cis als Quinte von Fis-Dur) aufzeigen, bei Beethoven erklingt an der entsprechenden Stelle durch den Liegeton es der ersten Violinen ein übermäßiger Klang (g-h-es). Dass es sich hierbei um eine Art ›erstarrten Vorhalt‹ eines G-Dur-Akkords handelt, der über den Skalenton d zu referenzieren wäre, ist musikalisch einleuchtend, sich ein gleichzeitiges Erklingen des Strukturtons d mit dem es der Violinen vorzustellen, dagegen unsinnig.

2.) Dem abgebildeten Beispiel Mozarts (Abb. 25 oberes Beispiel) geht eine sechstaktige I-V-Pendelharmonik voran (ihr folgt eine gleichlange Gestaltung des Quintabsatzes). Auch zu dem abgebildeten Abschnitt der Sinfonie Beethovens gehören noch 22 einleitende und zur Überleitung gehörige Takte. Sie haben die Funktion einer ›Orchesterwalze‹, also einer kontinuierlichen Steigerung vom piano bis zum fortissimo sowie der Entfaltung des Klangraums. Thematisch ist diese Taktgruppe durch Wiederaufgreifen des Hauptgedankens als Beginn der Überleitung kenntlich gemacht (vgl. hierzu S. 369 und Fußnote 30). Auch der bisher als Überleitung erörterten Passage aus KV 13 geht eine Taktgruppe (I-IV-I-V-I-Pendelharmonik) voran, für die es plausibel wäre, sie zur Überleitung zu zählen. Überleitungsabschnitten, die durch idealtypische Tonleiterausschnitte referenziert werden, können also eine oder sogar mehrere Taktgruppen vorausgehen, die sich in der Regel als Pendel- oder Kadenzmodelle verstehen lassen. Die bisher erörterten Überleitungsmodelle werden daher alle um die Möglichkeit einer ›Taktgruppe‹ erweitert, die vorhanden sein oder auch fehlen kann und deren Bezeichner ›Anderes‹ anzeigt, dass ihre Beschaffenheit hier nicht näher bestimmt worden ist.

Es wird behauptet:

5. Einige Überleitungen in Dur-Kompositionen Mozarts lassen sich als Kombination aus Tonleiterausschnitten mit mehr als vier Tönen (z.B. Pentachord, Hexachord, Heptachord etc.), einem Halbschluss sowie ggf. einer einleitenden Taktgruppe verstehen.

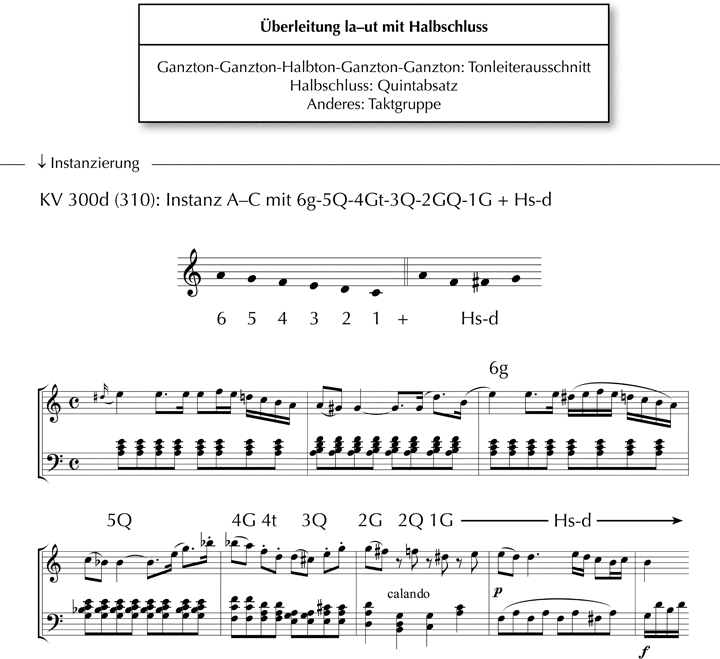
Die Benennung der Überleitungen erfolgt im Sinne der bisherigen Ausführungen (z.B. ›Überleitung sol–ut mit Halbschluss‹, ›Überleitung ut–fa mit Halbschluss‹, ›Überleitung la–ut mit Halbschluss‹ usw.).

Die Erweiterung des idealtypischen Pentachords zum Hexachord ist geeignet, die Überleitung einer Moll-Sonate zu beschreiben. Die Instanz einer ›Überleitung la–ut mit Halbschluss‹ prägt z.B. den Kopfsatz der Klaviersonate in a-Moll KV 300d (310) in den Takten 9–16:

Abb. 26: W.A. Mozart, Klaviersonate in a-Moll KV 300d (310), 1. Satz, T. 9–16

Jenem Abschnitt, der sich durch den Skalenausschnitt verstehen lässt (ab 6g), gehen auch in diesem Beispiel zwei Takte (T-D) voran. Thematisch wird hier mit der Wiederkehr des Anfangs der Beginn der Überleitung signalisiert. Diese beiden Takte lassen sich zwar auch als harmonische Prolongation des ersten Skalentons a beschreiben, doch soll hier – um unnötige Verkomplizierungen zu vermeiden – auf die Einführung von Undezimakkorden und eine entsprechende Chiffrierung verzichtet bzw. der Überleitungsbeginn wie in den vorangegangenen Beispielen unter ›Anderes‹ subsumiert werden.

Eine Überleitung, der ein idealtypisches Heptachord zugrunde liegt (›Überleitung ut–re mit Halbschluss‹), findet sich im ersten Satz der Violinsonate KV 317d (378)[33], Instanzen der ›Überleitung ut–ut mit Halbschluss‹ (vollständige ›regola‹-Ausarbeitungen), lassen sich im dritten Satz der genannten Violinsonate sowie im Kopfsatz der Sinfonie in D-Dur KV 385[34] (›Haffner‹) aufzeigen.

Abschließend sei hervorgehoben, dass auch die idealtypische Setzung von Tonleiterauschnitten mit weniger als vier Tönen sinnvoll ist. Das nachfolgende Diagramm zeigt die Überleitung aus dem Kopfsatz des Streichquartetts in F-Dur KV 168 und dem Schlusssatz der Sinfonie in D-Dur KV 73q (84):

Abb. 27: Streichquartett in F-Dur KV 168, 1. Satz, T. 13–18 und Schlusssatz der Sinfonie in D-Dur KV 73q (84), 1. Satz, T. 17–28

Äußeres Anzeichen für den Beginn der Überleitung im Streichquartett KV 168 sind die imitatorischen Einsätze. Sie wirken in Bezug auf die vorangegangenen Takte kontrastierend und signalisieren den Eintritt eines neuen Formteils auf eine vergleichbare Art wie die Wiederkehr des Hauptsatzes.[35] In der Sinfonie KV 73q (84) sind Überleitung und Hauptsatz dagegen aufgrund einer deutlichen Zäsur voneinander getrennt (Grundabsatz der Grundtonart). Diese Überleitung entspricht in ihrem Verlauf dem Beginn spezifischer Ausprägungen des Modells ›Überleitung fa–ut mit Halbschluss‹ (4GS-3T[…], vgl. hierzu die Überleitungen der Kopfsätze aus KV 45, 48, 73, 111, 112, 114, 159, 169, 315c u.v.a.), nur dass die idealtypisch möglichen Harmoniefolgen eines zweiten und ersten Skalentons (re–ut) fehlen. Es handelt sich hier also um Überleitungen, denen ein idealtypischer Verlauf aus zwei Tönen zugrundeliegt (2–1), die Bezeichnung ›Überleitungen fa–mi mit Halbschluss‹ verweist auf die strukturelle Nähe zu Überleitungen, die sich über den idealtypischen Tetrachord fa–ut beschreiben lassen.[36]

Es wird daher behauptet:

6. Einige Überleitungen in Dur-Kompositionen Mozarts lassen sich als Kombination aus Tonleiterausschnitten mit weniger als vier Tönen (z.B. Trichord, Dichord), einem Halbschluss sowie ggf. einer einleitenden Taktgruppe verstehen.

Die Benennung von Überleitungen mit drei und zwei Tönen erfolgt im Sinne der bisher entfalteten Systematik. Beispielsweise findet sich eine Instanz der ›Überleitung fa–mi mit Halbschluss‹ im Kopfsatz der Sinfonie in D-Dur KV 48 (T. 9–13 = 2GS-1T + HS-t), eine Referenz der ›Überleitung re–ut mit Halbschluss‹ prägt den ersten Satz der Violinsonate KV 11 (T. 7–10 = 2Q-1G + Hs-d) und eine ›Überleitung mi–ut mit Halbschluss‹ (T. 21–28 = 3Q:-2g:gQ:Q:-1G: + Hs-b) charakterisiert den letzten Satz der Sinfonie in G-Dur KV 124.

Insbesondere durch Überleitungen, die sich als ›Überleitung fa–mi‹ verstehen lassen, kann eine Brücke geschlagen werden zu jenen Menuetten, die Mozart in seiner Kindheit gespielt und komponiert hat. Denn das Harmoniemodell 2GS-1T oder 2tS-1T (mit 2–1 = fa–mi) findet sich in diesen Stücken charakteristischerweise in den Takten fünf und sechs bzw. fünf bis acht (z.B. in KV 1e und KV 1f sowie den jeweils ersten Menuette aus KV 6), also in vergleichbarer Formfunktion wie die gezeigten Überleitungen in ausgedehnteren Kompositionen. Im Interesse einer »Distanzierung der Vergleichsgesichtspunkte« sowie im Einklang mit einer zeitgenössischen Musikdidaktik[37] werden im Folgenden auch entsprechende Takte aus Menuetten als ›Überleitungen fa–mi‹ bezeichnet und in den Datenbestand der Referenzstellen integriert.

Zusammenfassung, Kritik und Internet-Projekt

In diesem Beitrag, der sich als Beginn einer wissenschaftlichen Untersuchung zum Formteil ›Überleitung‹ in der Musik Mozarts versteht, sind Behauptungen aufgestellt worden, die wie folgt zusammengefasst werden können:

1. Die Beschaffenheit einer großen Anzahl von Überleitungen in Dur-Kompositionen Mozarts wird reguliert durch die Möglichkeiten einer im Hinblick auf die Musiksprache des 18. Jahrhunderts sinnvollen Harmonisierung von Tonleiterausschnitten (2–1, 3–1, 4–1, 5–1, 6–1 etc.).

2. Einige Überleitungen in Dur-Kompositionen Mozarts lassen sich dabei vollständig mit Hilfe des Idealtyps ›Tetrachord‹ (fa–ut) beschreiben, während ein Großteil der Überleitungen sich als Kombination aus ›Tetrachord‹ und Halbschluss verstehen lässt.

3. Wenige Überleitungen in Dur-Kompositionen Mozarts erweisen sich als Kombination aus ›Dur-Tetrachord‹ (fa–ut) und Sequenz oder aus idealtypischem Tonleiterausschnitt mit mehr oder weniger als vier Tönen sowie einem Halbschluss.

4. Überleitungen der unter 1–3 beschriebenen Art können durch zusätzliche Taktgruppen erweitert werden.

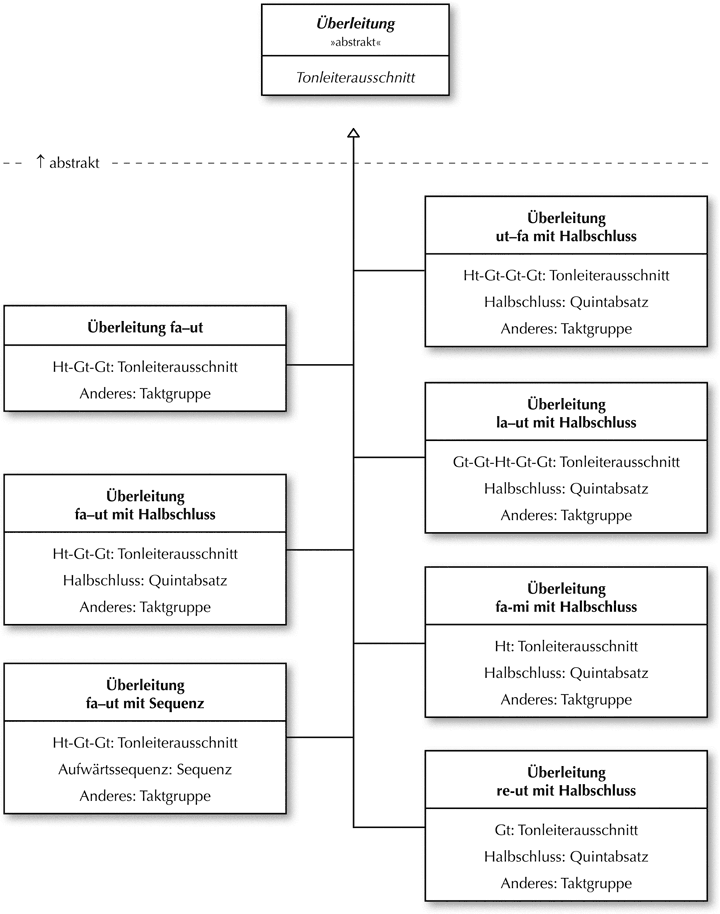
Zur Überprüfung dieser Sätze wurde eine Methode verwendet, die auf einen Modellbegriff rekurriert, der sich von einem in der Musiktheorie und Musikwissenschaft verbreiteten Modellverständnis unterscheidet. Das folgende Klassendiagramm zeigt das den Ausführungen zugrunde liegende Modelldesign:

Abb. 28: Klassendiagramm I – Überleitungen

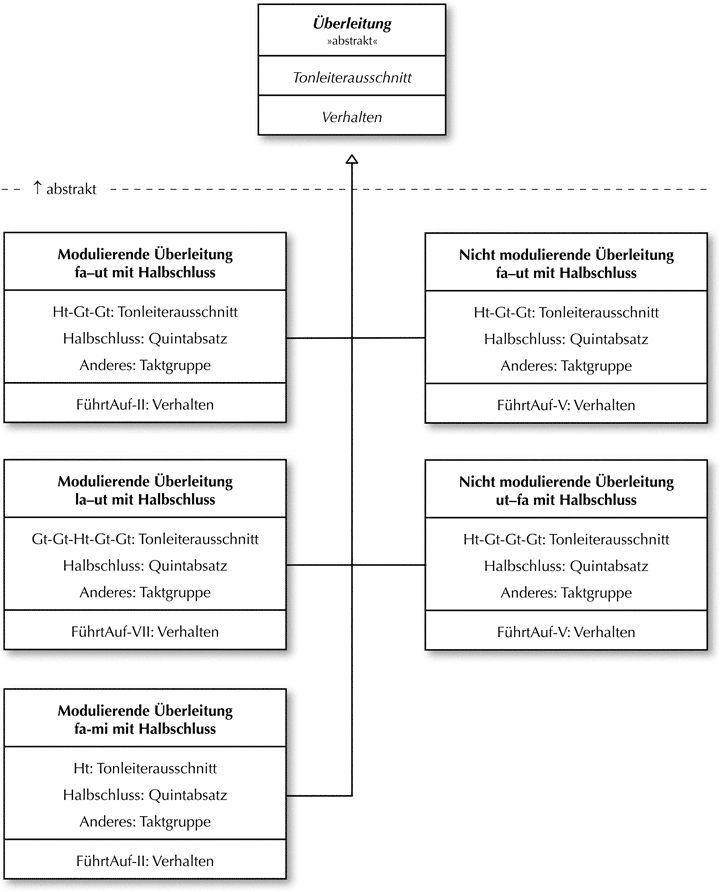
Für eine Erläuterung des UML-Diagramms[38] verweise ich auf meinen letzten Beitrag in der ZGMTH.[39] In diesem Beitrag hatte ich zudem ausgeführt, dass ein Modell auch durch ein spezifisches Verhalten charakterisiert wird. Als Verhalten von Überleitungen wurde jene Funktion angesprochen, die traditioneller Weise als ›modulierend‹ (Hinführung auf den II. Ton mit dominantischer Wirkung) oder ›nicht modulierend‹ (Hinführung auf den V. Ton mit dominantischer Wirkung) bezeichnet wird. Diese Funktion ist in erster Linie eine Kategorie der Rezeption und lässt sich nicht zwangsläufig als eine Eigenschaft des Tonsatzes beschreiben. Das Verhalten kann selbstverständlich in das Modelldesign integriert werden. Es bewirkt eine Differenzierung und Vermehrung der Anzahl von Modellen. Das folgende Klassendiagramm zeigt diese Differenzierung nur für eine Auswahl der Überleitungen mit Halbschluss:

Abb. 29: Klassendiagramm II – Überleitungen mit ›Verhalten‹

Die Entscheidung darüber, ob es sinnvoll ist, das Verhalten zu berücksichtigen, ist abhängig von pädagogischen Interessen bzw. der Art des Forschungsvorhabens. Für diesen Beitrag war das Verhalten von Modellen nicht von Bedeutung.

Da ein Denken von Modellen auf die hier beschriebene Art für die musikalische Analyse ungebräuchlich ist, sind Missverständnisse nicht auszuschließen. Folgende Einwände wären denkbar bzw. sind bereits schriftlich vorgebracht worden:

1. Ein objektorientiertes Modelldesign ermögliche unendlich viele Modelle, was wiederum den Ansatz für die Praxis unbrauchbar mache. Tatsächlich sind unendlich viele Modelle denkbar und ein Ausschließen von Modellen wäre Begrenzung durch Dogmatik. Auf der Ebene kleinster Modelle läuft jedoch kein Forschungsprogramm. Gearbeitet wird mit komplexen Einheiten, die aus Modellen bestehen, die wiederum aus Modellen bestehen etc., das heißt: Ein Denken in Modellen ist kaskadierend. In dem Klassendiagramm der Abb. 28 lässt sich der gezeigte Tonleiterausschnitt fa–ut als ionisches-Tetrachord (Modell) verstehen, andere Modelle des Typs ›Tetrachord‹ wären das phrygische und das dorische Tetrachord (la–mi bzw. sol–re). Die ›Aufwärtssequenz‹ ist ebenfalls ein komplexes Modell, das sich in vielfältige Sequenzmodelle aufspalten ließe, genauso wie der Halbschluss, der hier nur exemplarisch besprochen und das Platzhalter-Modell ›Anderes‹, dem hier so gut wie keine Aufmerksamkeit gewidmet worden ist (es ist allerdings unschwer sich vorzustellen, dass viele Aussagen über dieses Modell hätten getroffen werden können). Die genannten Modelle sind Bestandteil des Modells ›Überleitung fa–ut mit Halbschluss‹, welches wiederum von dem abstrakten Modell ›Überleitung‹ die Eigenschaft ›Tonleiterausschnitt‹ (und ggf. ein Verhalten) erbt. Erst auf den letzten Ebenen der Abstraktion wird man hinsichtlich der Musik Mozarts voraussichtlich mit einigen wenigen Überleitungsmodellen operieren können, wobei von entscheidender Bedeutung ist, dass für die vielen nicht spezifizierten Modelle jederzeit die Möglichkeit besteht, sie zu beobachten und somit zum Gegenstand der Forschung zu erheben.

2. Folker Froebe schrieb in der letzten Ausgabe der ZGMTH:

Vielmehr scheint die Behandlung von Intervallkonsekutiven, kanonischen Gerüstsätzen, Klauseln, Bassformeln, Generalbassmodellen, Figuren etc. in verschiedenen Lehrkontexten und Teildisziplinen der Komplexität und strukturellen Vernetzung der Phänomene in mancher Hinsicht eher gerecht zu werden, als eine generalisierende Rede von Modellen oder ›Topoi‹, die heterogene Aspekte – Satztechnik, Tonalität, Formfunktion und Kontextualisierung, Stil und Semantik – subsumiert oder in eins zu setzen sucht. Gegenwärtigen Bestrebungen zur Differenzierung des Modellbegriffs böte die historische Theoriebildung wertvolle Anknüpfungspunkte.[40]

Im Sinne der vorangegangenen Ausführungen sprechen die von Folker Froebe genannten Aspekte (»Intervallkonsekutiven, kanonischen Gerüstsätzen, Klauseln, Bassformeln, Generalbassmodellen, Figuren etc.«) nicht gegen das Denken von Modellen in dem hier dargelegten Sinne. Ungeachtet des Werts historischer Theoriebildung als Impulsgeber für das Entwickeln von Modellen darf bezweifelt werden, dass historische Traktate die richtigen Ratgeber für ein modernes objektorientiertes Denken sind.

3. Es ist zu vermuten, dass Martin Eybl wie auch Folker Froebe nicht hinreichend zwischen einem Modell (als Äquivalent einer Klasse objektorientierter Programmiersprachen) und einem Satzmodell herkömmlicher Art unterscheiden. In seiner Rezension zu meinem Buch ›Die Notenbücher der Mozarts‹ schrieb Martin Eybl:

Wo sich die Modelle ohne spezielle Stimmführung nur mehr auf elementare Harmoniefolgen beschränken, wie etwa das Pendeln zwischen der Tonika und einem anderen Klang (»IV-I-Modelle«: 188–193; »V-I-Modelle«: 193–197), verliert die Zusammenstellung an Prägnanz. Das Bestreben, den gesamten Tonsatz auf Modelle zurückzuführen, verrät eine gewisse Systematisierungswut. An einer Stelle erwägt der Autor etwa ernsthaft die Einführung einer »gesonderte[n] Kategorie Orgelpunktmodelle« (294/95). Vielleicht kommen wir dem Gegenstand aber näher, wenn wir uns tonale Musik als ein Gefüge profilierter Satzmodelle in Kombination mit Abschnitten vorstellen, die einfach bestimmten Regeln gehorchen, ohne auf tradierte komplexe Einheiten (›Modelle‹) zurückzugreifen. Man müsste dann nicht notwendig bei jeder Note auf Satzmodelle rekurrieren.[41]

In meinen Arbeiten zu Mozart bemühe ich mich nicht um die Deutung von Satzmodellen, sondern von jenen Abschnitten, »die einfach bestimmten Regeln gehorchen«. Doch welchen? Martin Eybls Ansicht, dass die Zusammenstellung von Modellen z.B. mit dem ›IV-I-Modell‹ (= Überleitung fa–mi in der Terminologie dieses Beitrags) an Prägnanz verliert, lässt sich nachvollziehen, wenn man an einfache Akkordverbindungen denkt. Dagegen dürften die Ausführungen in diesem Beitrag zu den Überleitungen der Abbildung 27 noch einmal verdeutlicht haben, dass es mir nicht um einfache Akkordverbindungen (bzw. Satzmodelle), sondern um idealtypische Konstruktionen (Modelle) geht, die das Referenzieren komplexer musikalischer Einheiten und deren Vergleichung als Grundlage einer seriösen Stilforschung ermöglichen.

Die harmonische Betrachtung wurde aus zwei Gründen zum Schwerpunkt dieser Untersuchung gewählt: Zum einen sind Aussagen zur Harmonik von Überleitungen und Durchführungen ein Desiderat der Sonatentheorie, das immer noch dem Vorurteil Vorschub leistet, hier herrschte allein Inspiration, wenn nicht gar kompositorische Willkür. Zum anderen hätte eine ebenso sorgfältige Untersuchung zu Stimmführung, motivischer Ausarbeitung und Metrik die Grenzen dieses ohnehin umfangreichen Aufsatzes vollends gesprengt. In der nordamerikanischen Literatur wurden in dieser Hinsicht bereits einige Überlegungen systematisiert[42], weiterführende Arbeiten wären hier wünschenswert.

Ein kleineres Problem dieser Untersuchung bestand darin, dass alle Akkorde, die einen Halbschluss vorbereiten, auch unter den ersten Skalenton subsumiert werden können, denn dieser ist Antepenultima der unterbrochenen Sopranklausel des Halbschlusses. Im Beispiel der Sonate op. 10, Nr. 2 von Ludwig v. Beethoven wäre es z.B. möglich gewesen, den ersten Skalenton zu prolongieren (1GtqS = C als C-Dur, a-Moll, fis-vermindert und D-Dur) und einen metrischen Kadenzeintritt zu vermuten. Dieser Weg wurde nicht beschritten, sondern pragmatisch so verfahren, dass alle Harmonien ab der ersten Harmonie des ersten Skalentons, der keine bidirektionale Bewegung mehr folgt, als Vorbereitung der Kadenz interpretiert worden sind.[43]

Ein schwerwiegenderes Problem liegt in der Entscheidung, eine Chromatisierung von Tetrachordtönen zuzulassen. Es ist leicht ersichtlich: Im Kopfsatz der Sonate KV 570 wurde eine Chromatisierung des Tetrachords b-a-g-f zu b-as-g-f als akzidentielle Verfärbung interpretiert, was zur Folge hatte, dass diese Überleitung als Instanz des Modells ›Überleitung fa–ut mit Halbschluss‹ begriffen werden konnte. Doch nach welchen Kriterien erfolgt dann eine Unterscheidung zwischen der ›Überleitung fa–ut mit Halbschluss‹ und akzidentiell verfärbtem ›mi‹ und dem Modell ›Überleitung sol–re mit Halbschluss‹? Das Problem ist musikalischer (bzw. psychologisch-soziologischer) Natur und historisch über die Begriffe ›zufällig‹[44] (Kirnberger), ›willkührliche‹, ›durchgehende‹ oder ›förmliche Ausweichung‹[45] (Koch) greifbar. In älteren Praecepta spiegelt es sich in Anweisungen, Alterationen ohne Mutation (Hexachordwechsel) zu singen.[46] Die hier vorgeschlagene Lösung scheint derzeit trotz des Interpretationsspielraums angemessen, ob sie bis zum Abschluss der Untersuchung revidiert werden muss, bleibt abzuwarten.

Die in diesem Beitrag getroffenen Aussagen sind nicht nur im Hinblick auf die Chromatisierung als vorläufig zu erachten, da sie erst dann belastbar sein können, wenn unter der Forschungsperspektive alle Werke Mozarts in den Blick genommen worden sind. Eine solche Untersuchung dürfte die Möglichkeiten von Einzelpersonen vermutlich überschreiten, aus diesem Grund habe ich ein datenbankgebundenes Formular[47] im Internet eingerichtet, das Eingaben zu Überleitungen Mozarts auf die hier beschriebene Art ermöglicht. Öffentlich zugänglich sind darüber hinaus Abfragemöglichkeiten zu Harmoniefolgen, Skalenausschnitten etc., die gegebenenfalls bei der Lösung individueller Fragestellungen und anderer Forschungsvorhaben behilflich sein können.

Wenn zu den hier beschriebenen Modellen umfassende Ergebnisse vorliegen, wird sich zeigen, wie viele Überleitungen Mozarts sich mit den hier entfalteten Modellen angemessen erklären lassen und für welche Überleitungen weitere Modelle zu entwickeln sind. Es ist nicht unwahrscheinlich, dass diesen Überleitungen aufwärts führende Skalenbewegungen zu Grunde liegen. Beide Bewegungsarten – in Verbindung mit einem schrittweisen Verlauf – wären jedenfalls äußerst plausibel im Hinblick auf die Generalbasspraxis der Zeit.