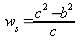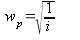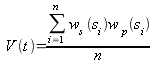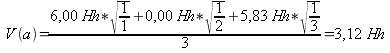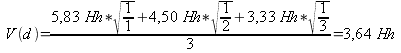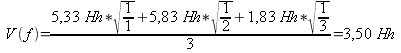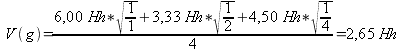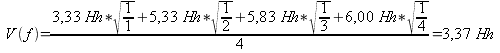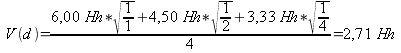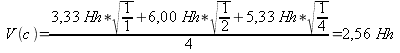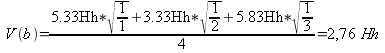Modelle der Akkordgrundtonbestimmung
Karl Traugott Goldbach
Die Bestimmung des Akkordgrundtons ist für die meisten neuzeitlichen Harmonielehren von entscheidender Bedeutung. Die erweiterte Tonalität des späten 19. und frühen 20. Jahrhunderts ließ die Grundtonbestimmung jedoch zum Problem werden. Um entsprechende Musik unter Einschluss traditioneller Verfahren erklären zu können, entwickelten Komponisten wie Paul Hindemith in ihren Tonsatzlehren unter anderem auch neue Methoden der Grundtonbestimmung. In jüngerer Zeit leitete der Psychoakustiker Ernst Terhardt aus seinen Forschungen zu ›virtuellen Grundtönen‹ ein Modell zur Bestimmung von Akkordgrundtönen ab, das Richard Parncutt, Llorenç Balsach und Ludger Hofmann-Engl jeweils weiterentwickelten. Am Beispiel dreier in der Jazz- und Popmusik häufig verwendeten Akkordfolgen – also eindeutig tonalen Verbindungen – werden in diesem Aufsatz alle sieben Modelle auf ihre Belastbarkeit getestet.
Einleitung
Jean Philippe Rameau stellte in seinem Traité de l’harmonie Experimente am Monochord vor, bei denen er eine Saite mit der Tonhöhe C in 1, 2, 3, 4, 5, 6 und 8 Abschnitte teilte und so die Töne C-c-g-c1-e1-g1-c2 erhielt.[1] Aus dieser Begründung des Durdreiklangs folgerte er zugleich die Prinzipien der Akkordumkehrung, der Terzschichtung[2] sowie seine Fundamentalbass-Lehre[3], an welche die meisten neuzeitlichen Harmonielehren anknüpfen. Bekanntlich stößt diese Lehre jedoch an Grenzen, wenn sie Akkorde erklären soll, die über einfache Drei- oder Vierklänge hinausgehen. Dies zeigt sich beispielsweise in Arnold Schönbergs Harmonielehre, der den (bei ihm ›Fundamentfolge‹ genannten) Fundamentalbass voraussetzt.[4] Er führt Akkordbildungen, die über den Nonenakkord hinausgehen, nicht mehr auf einen terzweisen Aufbau zurück, obwohl dies, wie er selbst einräumt, den Vorteil hätte, »daß man, ohne die Kontrolle der Fundamentschritte zu verlieren, manches noch ins System brächte, was heute draußen liegt, bei den zufälligen Harmoniebildungen«.[5] Entsprechend deutet er in seinem Kapitel über ›Quartenakkorde‹ zwar die Möglichkeit an, den Akkord d-g-c als Umkehrung einer Grundgestalt c-g-d aus der Obertonreihe herzuleiten, verwendet in diesem Abschnitt aber keine Stufenbezeichnungen mehr.[6] Dagegen behauptet Paul Hindemith im theoretischen Teil seiner Unterweisung im Tonsatz den (bei ihm ›Stufengang‹ benannten) Fundamentalbass für »die Musik aller Stilarten und aus allen Zeiten« nachweisen zu können.[7] Seine Analysen umfassen nicht nur Beispiele der dur-moll-tonalen Musik wie Bachs dreistimmige Invention in f-Moll[8] und Wagners Tristan-Vorspiel[9], sondern auch Schönbergs Klavierstück op. 33a.[10]
Mit den anderen in diesem Aufsatz vorgestellten Ansätzen zur Grundtonbestimmung teilt Hindemiths Theorie ein weiteres Erbe der Musiktheorie Rameaus. Auf einen Hinweis von Louis Bertrand Castel in dessen Rezension des Traité, dem nach die akustischen Untersuchungen Joseph Sauveurs die Thesen Rameaus stützten[11], übernahm letzterer das Konzept der Obertonreihe in seine Musiktheorie.[12] Während die französische Musiktheorie zu Beginn des 19. Jahrhunderts sich teilweise demonstrativ von naturwissenschaftlichen Begründungen abwandte[13], initiierte die bahnbrechenden Schrift Die Lehre von den Tonempfindungen als physiologische Grundlage einer Theorie der Musik des Physikers Hermann von Helmholtz zumindest für den deutschsprachigen Raum einen Paradigmenwechsel. Helmholtz versuchte auf Grundlage der Obertonreihe nicht nur Harmonik und Melodik, sondern auch die Klangfarbe zu erklären. Zugleich aber betonte er,
[…] daß das System der Tonleitern, der Tonarten und deren Harmoniegewebe nicht bloß auf unveränderlichen Naturgesetzen beruht, sondern daß es zum Teil auch die Konsequenz ästhetischer Prinzipien ist, die mit fortschreitender Entwickelung der Menschheit einem Wechsel unterworfen gewesen sind und ferner noch sein werden.[14]
Trotz dieser Mahnung treten immer wieder Autoren mit dem Anspruch auf, sie könnten die Musiktheorie aufgrund naturwissenschaftlicher oder psychologischer Erkenntnisse empirisch eindeutig begründen. Ein Beispiel hierfür sind die in diesem Aufsatz evaluierten Ansätze, aus dem psychoakustischen Konzept des ›virtuellen Grundtons‹ eine Methode zur Bestimmung von Akkordgrundtönen zu gewinnen. Da diese Modelle der Psychoakustiker Ernst Terhardt und Richard Parncutt sowie der Komponisten Llorenç Balsach und Ludger Hofmann-Engl implizit auf bestimmte Argumente zurückgreifen, die in Bezug auf die Obertonreihe in musiktheoretischen Begründungen stets wiederkehren, stehen zu Beginn dieses Aufsatzes die Herleitungen des Dur- und Mollakkords aus der Obertonreihe bei Hermann von Helmholtz und Arthur von Oettingen. Es folgen Anmerkungen zu Paul Hindemiths bereits erwähntem Modell zur Akkordgrundtonbestimmung.
Hermann von Helmholtz und Arthur von Oettingen
Der Durakkord lässt sich in seiner Grundstellung als 4., 5. und 6. Ton der Partialtonreihe auffassen. Für die Grundtonbestimmung bedeutet das nach Helmholtz:
In einem Durakkord c-e-g können wir g und e als Bestandteile des c-Klanges ansehen, aber weder c noch g als Bestandteile des e-Klanges, und weder c noch e als solche des g-Klanges. Der Durakkord c-e-g ist also ganz eindeutig; er kann nur mit dem Klang des c verglichen werden, und deshalb ist c der herrschende Ton in dem Akkord, sein Grundton, oder nach Rameaus Bezeichnung sein Fundamentalbaß, und keiner der beiden anderen Töne des Akkordes hat das geringste Recht, diese Stelle einzunehmen.[15]
Dagegen finden wir den Mollakkord, zumindest in reiner Stimmung, erst sehr spät in der Partialtonreihe, als 10., 12. und 15. Ton. Daher schlug Helmholtz vor, den Mollakkord als ›Mischklang‹ zu betrachten: Da im c-Moll-Akkord die Quinte g sowohl Bestandteil des c als auch des es ist, sieht er g als abhängigen Ton eines Akkordes an, der sowohl ein c-Klang mit zugefügtem es als auch ein es-Klang mit hinzugefügtem c sein könne.[16]
Beispiel 1: Herleitung des Molldreiklangs nach Hermann von Helmholtz 1913
Diese Interpretation stieß bei Musikern, die weiterhin von der Gleichberechtigung von Dur und Moll ausgehen wollten, auf Ablehnung, wie Helmholtz selbst in späteren Auflagen der Lehre einräumte.[17]
Den für die weitere musiktheoretische Diskussion wichtigsten Einwand machte Helmholtz’ Physikerkollege Arthur von Oettingen: Helmholtz definiere zwar einerseits den Mollakkord als Mischklang, weil der Grundton einer der Akkordtöne sein müsse, ordne aber andererseits dem Akkord aus den Tönen h-d-f-a den wieder rein aus der Obertonreihe hergeleiteten Grundton g zu.[18] Von Oettingens Berechnung des Grundtons hingegen stützt sich auf die Frequenzverhältnisse der Akkordtöne:
Sind zwei Töne durch zwei ganze Zahlen, a und b, (a<b), gegeben, und sind dieselben relativ zueinander, so ist 1 der tonische Grundton, da a und b Vielfache von 1 sind, keine Zahl aber zwischen 1 und a in beiden zugleich enthalten ist, da sonst letztere nicht relativ prim sein könnten.[19]
Somit kommt von Oettingen für den C-Dur-Dreiklang c1-e1-g1 mit dem Verhältnis 4:5:6 zum Grundton 1=C, für den c-Moll-Dreiklang c1-es1-g1 mit dem Verhältnis 10:12:15 zum Grundton 1=As.[20] Da von Oettingen hierin keine hinreichende Lösung sah, setzte er gegen die von ihm ›Tonigkeit‹ genannte Grundtonbezogenheit des Durdreiklangs eine von ihm ›Phonigkeit‹ genannte Obertonbezogenheit des Molldreiklangs: So wie die Töne des C-Durdreiklang den gemeinsamen Grundton C besitzen, enthalten die Obertonreihen der Töne des c-Molldreiklangs alle den Oberton g.[21]
Beispiel 2: Herleitung des Molldreiklangs nach Arthur von Oettingen 1866
Jeder Akkord hat demnach sowohl einen ›tonischen Grundton‹ als auch einen ›phonischen Oberton‹. Während sich der Dur-Akkord aus seinem ›tonischen Grundton‹ ableitet, generiert sich der Moll-Akkord aus seinem ›phonischen Oberton‹, weshalb von Oettingen und im Anschluss an ihn Hugo Riemann den c-Moll-Dreiklang auch von diesem Bezugston ausgehend als g° bezeichneten. Freilich nannte keiner der beiden Theoretiker den ›phonischen Oberton‹ jemals ›Grundton‹.[22]
Dafür finden wir bei Riemann ein Aufeinandertreffen zweier akustischer Phänomene, die beide im 20. Jahrhundert zur Begründung von Akkordgrundtonbestimmungen herangezogen wurden: den Kombinationston und den ›virtuellen Grundton‹. Bei laut erklingenden Intervallen nimmt das menschliche Ohr durch eine lineare Verzerrung auf dem Weg der Klangübertragung zusätzlich zu den real erklingenden Tönen Kombinationstöne wahr. Dabei ergeben sich Kombinationstöne 1. Ordnung zweier Einzeltöne f1 und f2 aus der Differenz f2-f1, Kombinationstöne 2. Ordnung aus der Differenz 2f1-f2.[23] Riemann vollzog mit seinem Harmonium Helmholtz’ Experimente nach[24] und stimmte dafür über dem C die ersten dreizehn Partiale in reiner Stimmung. Da diese jeweils Vielfache der Grundfrequenz sind, ist bei aufeinanderfolgenden Tönen der Partialtonreihe jeweils der Grundton Kombinationston. So beträgt die Differenz zwischen den 5. und 6. Partial 6-5=1, zwischen dem 6. und 7. Partial 7-6=1.[25] Doch Riemann stellte nun fest, »daß auch Intervalle, welche nicht nebeneinander liegenden Tönen der Reihe entsprachen, den Combinationston C deutlich hören ließen«, während die nach Helmholtz eigentlich zu erwartenden Töne viel leiser waren.[26] Was Riemann hörte, ist ein den Kombinationstönen verwandtes, zu dieser Zeit aber noch nicht beschriebenes Phänomen, der ›virtuelle Grundton‹, auch ›Residualton‹ genannt:[27] Menschliche Hörer hören fehlende Teiltöne in einem Spektrum ›hinzu‹ und erkennen deshalb beispielsweise am Telefon die Stimme ihrer Gesprächspartner, obwohl das Telefon die tiefen Grundfrequenzen der menschlichen Stimme gar nicht überträgt. Ab vier simultan gegebenen Teiltönen einer Partialtonreihe ist der Grundton deutlich zu hören. Unter bestimmten Voraussetzungen lässt sich der virtuelle Grundton aber auch schon bei einem Stimulus aus nur zwei Teiltönen wahrnehmen.[28] Riemann interpretierte seine Beobachtung fälschlicherweise als Beweis für die »objektive Existenz der Untertöne in der Schallwelle«.[29] Dabei sollte die Untertonreihe der Obertonreihe entgegengesetzt sein und somit endlich eine befriedigende physikalische Erklärung auch des Molldreiklangs bieten: Riemanns Rekonstruktion der akustischen Natur war durch das Interesse geleitet, das Konzept des ›harmonischen Dualismus‹ naturwissenschaftlich zu untermauern.[30]
Paul Hindemith
Das Konzept des ›virtuellen Grundtons‹ war Hindemith unbekannt, und er entwickelte seinen Versuch einer systematischen Musiktheorie aus einem eigenen Verständnis der Kombinationstöne heraus. Während Diether de la Motte Hindemiths Kompositionen vor der Theorie ihres Schöpfers in Schutz nehmen möchte und an Hindemiths Kompositionen ein eigenes Verfahren entwickelt, das ›harmonische Gefälle‹ analytisch nachzuweisen[31], haben Hindemiths Theorien Bernhard Billeter zufolge trotz falscher und willkürlicher Grundlagen »zu einem sehr brauchbaren Lehrgebäude geführt«.[32] Umstritten ist bereits seine Methode zur Grundtonbestimmung: Obwohl z.B. William Thomson einräumt, die empirische und methodische Begründung sei falsch, hebt er hervor, sie sei ein Fortschritt gegenüber der traditionellen Begründung der Akkorde als Terzschichtungen – entsprechend hätten die meisten zeitgenössischen Musikanalytiker Hindemiths Ansatz übernommen.[33] Dagegen lehnen Dieter Nowka und Andreas Holzer das Verfahren wegen ihrer Meinung nach nicht nachvollziehbarer Ergebnisse ab.[34]
Um den Grundton von Akkorden zu bestimmen, geht Hindemith von einer Bestimmung des Grundtons bei Intervallen aus. Zunächst gewinnt er eine Reihe aus Intervallpaaren, die jeweils den gleichen (oktavversetzten) Bestand an Kombinationstönen 1. und 2. Ordnung haben. Diese Intervallpaare ordnet er nach ihrem Dissonanzgrad: Quinte und Quarte (beide Kombinationstöne sind mit einem der Intervalltöne oktavidentisch)[35], große Terz und Sexte (einer der Kombinationstöne ist mit einem Intervallton identisch ist und der andere ergänzt das Intervall zu einem Dreiklang ergänzt)[36], kleine Terz und große Sexte (die Kombinationstöne ergänzen das Intervall zu einem Dreiklang)[37] und Sekunden und Septimen (die Kombinationstöne geben nur »ungenaue Aufschlüsse« über den Intervallgrundton).[38] Die ›Flanken‹ der Reihe bilden schließlich die Oktave und der Tritonus, die beide mit keinem anderen Intervall ein Paar bilden.[39]
Beispiel 3: Dissonanzgrad der Intervalle bei Paul Hindemith 1940
Bei dem jeweils ersten Intervall eines dieser Paare ist Hindemith zufolge der untere Ton Grundton des Intervalls, bei dem jeweils zweiten der obere Ton. Für die ersten beiden Paare begründet er dies mit den vorhandenen Kombinationstönen, für die beiden anderen Paare legt er die Grundtöne in Analogieschlüssen fest.[40] Der Grundton eines Akkordes ist jeweils der Grundton des ›besten‹ oder ›wertvollsten‹ (konsonantesten) Intervalls; ist das Intervall mehrfach vorhanden, dient das tiefste zur Grundtonbestimmung.[41] Dabei ist es gleichgültig, »ob der zum Grundton gehörige Intervallergänzungston in der gleichen, in einer darüberliegenden Oktave (bei Quinten, Terzen, Septimen) oder weit unterhalb (bei Quarten, Sexten, Sekunden) zu finden ist«.[42] Dieses Vorgehen ist allerdings häufig unplausibel. So kritisiert Dieter Nowka am folgenden Beispiel Hindemiths[43], bei dem der erste Akkord zugleich die unteren sechs Töne der übrigen drei beisteuert, es sei schwer einzusehen, »weshalb bei einfacher Terzerweiterung nach oben sich der Grundton von a’ nach e’ verlagern soll«.[44]
Beispiel 4: Grundtöne komplexer Akkorde bei Paul Hindemith 1940
Nicht nur in komplexen Akkorden kann das Hinzufügen oder Weglassen einzelner Akkordtöne in einer Grundtonbestimmung nach Hindemith zu unterschiedlichen Ergebnissen führen, sondern auch in einfachen und eindeutig tonalen Harmonieverbindungen der Jazz- und Popmusik. Jazz-Musik baut häufig auf sogenannten ›II-V-I-Verbindungen‹ auf:
Beispiel 5: Grundtonbestimmung in einer fünfstimmigen II-V-I-Verbindung nach Paul Hindemith
Der II- und der I-Akkord sind für eine Grundtonbestimmung nach Hindemith unproblematisch, da alle Basstöne dieser Kadenz von ihren Quinten begleitet werden. Dem V-Akkord ist jedoch neben Septime und None auch noch eine Terzundezime hinzugefügt, dafür fehlt die Quinte. Das ›beste Intervall‹ im Akkord der V. Stufe ist somit die Quinte a1-e2; demnach wäre a1 der Grundton des Akkordes. Wenn wir die fünfstimmige Akkordverbindung zur Vierstimmigkeit reduzieren, wird wegen der Quarte h-e2 das e2 zum Grundton. Auch bei den beiden anderen Akkorde verliert der Basston seine Stellung als Grundton, da hier jeweils die Quarten c1-f1 und h-e1 die ›besten‹ Intervalle sind. Die V. und die I. Stufe bekämen den vermeintlich Grundton e:
Beispiel 6: Grundtonbestimmung in einer vierstimmigen II-V-I-Verbindung nach Paul Hindemith
Betrachten wir eine weitere Akkordfolge, wie sie zum Beispiel Carole King gerne verwendet.[45]
Beispiel 7: Grundtonbestimmung in einer Kadenz aus Will You Love me Tomorrow von Carol King nach Paul Hindemith
Nach Hindemith wäre die Quarte c1-f1 das ›beste‹ Intervall des Akkordes und damit f1 der Grundton. Dies entspricht einer in der Popmusik häufigen ›Leadsheet‹-Schreibweise des Akkordes als F-Dur mit G im Bass: F/G. Doch deutet der Quartanstieg im Bass vielmehr auf eine Dominant-Tonika-Verbindung hin, womit der erste Akkord auch als Dominant-Sept-Non-Undezim-Akkord verstanden werden kann, dem Terz und Quinte fehlen (im Beispiel durch die ausgefüllten Notenköpfe angedeutet):
Beispiel 8: Der 1. Akkord der ›Carole-King-Kadenz‹ als Terzschichtung
Fügen wir diesem Akkord die Quinte d1 hinzu, dann wäre auch nach Hindemith G Akkordgrundton.
Die folgende Harmonieverbindung lehnt sich an die Harmonik der Strophen im Titel Spinning Wheel von Blood, Sweat and Tears an:[46]
Beispiel 9: ›Spinning-Wheel-Kadenz‹ nach Paul Hindemith
Auch hier fehlen den Akkorden die Quinten über dem Bass, während in den beiden Oberstimmen jeweils Quarten liegen; demnach ist der Stufengang mit der Oberstimme identisch: Ausgerechnet jene Töne, welche die Funktionsanalyse als zusätzliche Töne deutet, sind für Hindemith Akkordgrundtöne, obwohl sie in der Oberstimme und vom jeweiligen funktionalen Grundton weit entfernt liegen. Andreas Holzer stellt zu Recht fest: »Willkür herrscht bei der Bewertung der Akkorde, nicht einsehbar ist die Rekrutierung eines Akkordgrundtons aus dem ›besten Intervall‹ im Akkord.«[47]
Ernst Terhardt
Ernst Terhardts Modell zur Grundtonbestimmung ist ein Nebenprodukt seiner langjährigen psychoakustischen Forschungen zu ›virtuellen Grundtönen‹, das er als Beitrag zu einer interdisziplinären Festschrift veröffentlichte.[48] Jedoch verhinderte in der (meist englischsprachigen) psychoakustischen Forschung, in der Terhardt ansonsten häufig zitiert wird, die Deutschsprachigkeit seines Aufsatzes die internationale Rezeption. Abgesehen von den Weiterentwicklungen seines Modells durch Richard Parncutt und Ludger Hofmann-Engl bzw. der Rezeption durch Llorenç Balsach bezieht sich die englischsprachige Forschung daher meist auf Publikationen Terhardts, die Algorithmen für die Bestimmung von ›virtuellen Grundtönen‹ in komplexen Tönen und Sinustongemischen beschreiben.
Terhardt zufolge beherrschen die Akkordgrundtöne die Musikwahrnehmung, den musikalischen Satz und die Musikanalyse, doch die Erklärung des Wesens der Grundtöne, ihre psychoakustischen Grundlagen sowie ihre algorithmische Bestimmung seien bislang unklar geblieben.[49] Rameaus Erklärung durch das Prinzip des Terzenaufbaus sei willkürlich, Grundtonbestimmungen der funktionalen Harmonik nach Riemann eher durch Intuition als durch klare Regeln beherrscht und Hindemiths Zurückführung der Grundtöne auf Kombinationstöne mit Sicherheit falsch.[50] Daher schlägt Terhardt eine Übertragung der Ergebnisse zur Forschung an ›virtuellen Grundtönen‹ auf die Akkordgrundtonbestimmung mit dem Argument vor, beide Erscheinungen seien »wesensgleich«.[51]
Terhardt verweist auf Beobachtungen zur Tonhöhenwahrnehmung bei Glocken, deren Teiltöne teilweise in einem unharmonischen Verhältnis zueinander stehen. Dennoch ordnen ihnen Probanden im Experiment durch Frequenzabgleich mit einem Sinuston den sogenannten ›Schlagton‹ zu, der im folgenden Beispiel für die wichtigsten Teiltöne einer historischen Kirchenglocke im Frequenzspektrum überhaupt nicht enthalten ist:[52]
Beispiel 10: ›Schlagton‹ einer Glocke nach Ernst Terhardt
Terhardt zufolge liegt dieses Prinzip auch der Wahrnehmung der Grundtöne von Akkorden zugrunde, jedoch erläutert er den Schritt von der Bestimmung des Schlagtons in einem Gemisch von Sinustönen, die in einem unharmonischen Verhältnis zueinander stehen, zur Bestimmung des Grundtons eines aus komplexen Tönen bestehenden Akkords nicht näher. Aus psychoakustischen Messungen und Experimenten, die er ebenfalls nicht erläutert, leitet er weitere Prämissen ab.[53] Die »allgemein als Bezugssystem akzeptiert[e]« temperierte Stimmung dient als Grundlage, da »die in den realisierten Akkordtönen unvermeidlich auftretenden Grundfrequenzabweichungen von der Normalstimmung so klein sind, daß sie für die Bildung der ›Virtuellen Tonhöhe‹ bzw. der Grundtöne keine wesentliche Rolle spielen«, was wiederum durch psychoakustische Beobachtungen gestützt sei. Außerdem sollen die einzelnen Akkordtöne jeweils harmonisch komplexe Töne (periodische Schallsignale) sein, bei denen mindestens die erste und zweite harmonische Schwingung relevante Teiltöne sind; dies sei »bei den gebräuchlichen musikalischen Klangerzeugern« der Fall.[54] Zur Vereinfachung lässt Terhardt die Existenz des dominanten Frequenzbereiches in einem harmonisch komplexen Ton außer acht: »Unter den genannten Voraussetzungen ist das tonale Bezugssystem des gesamten Grundtonwahrnehmungsvorganges durch die ersten zehn Harmonischen, angenähert durch Töne der Halbtonskala, gegeben«.[55]
Terhardt stellt nun für jeden Akkordton dessen erste zehn ›Subharmonischen‹ als potentielle Grundtöne fest, also jene Töne, für die der Akkordton als einer der ersten zehn Obertöne erscheint. Da jeweils der 1., 2., 4. und 8., der 3. und 6., sowie der 5. und 10. Teilton oktavverwandt sind, hat jeder Akkordton fünf potentielle Grundtöne. Anhand von fünf aufeinander folgenden Schritten bestimmt Terhardt den Akkordgrundton:
(1) Man schreibe die Akkordtöne horizontal nebeneinander (der Übersicht wegen werden Akkordtöne durch Kleinbuchstaben, Grundtöne durch Großbuchstaben bezeichnet.)
(2) Unter jeden der Akkordtöne schreibe man die fünf dazugehörigen Grundtonkandidaten. Dieselben ergeben sich wie folgt. Der erste Kandidat ist dem Notensymbol nach identisch mit dem dazugehörigen Akkordton (unison); der zweite liegt eine Quinte, der dritte ein große Terz darunter; der vierte einen Ganzton darüber, und der fünfte einen Ganzton darunter.
(3) Man suche die miteinander übereinstimmenden Grundtonkandidaten. Besteht ein Akkord aus n verschiedenen Tönen, so kann maximal n-fache Koinzidenz auftreten. Der zugehörige Grundton wird in diesem Falle als vorherrschend angesehen und als Grundton n-ten Grades bezeichnet. Grundtöne, die sich aus einer geringeren Zahl von Koinzidenzen ergeben, werden ebenfalls als relevant, jedoch weniger gewichtig angesehen. Sie werden sinngemäß als Grundton (n-1)-ten Grades, usw. bezeichnet.[56]
Für einen C-Dur Dreiklang ergibt sich so folgende Tabelle:
Akkordtöne: | c | e | g |
Unisono: | C | E | G |
- Quinte: | F | A | C |
- große Terz: | As | C | Es |
+ große Sekunde: | D | Fis | A |
- große Sekunde: | B | D | F |
| |||
Grundton 3. Grades: | C | ||
Grundtöne 2. Grades: | F, D, A | ||
Tabelle 1: Akkordgrundtöne für den C-Dur-Dreiklang nach Terhardt 1982
Da Terhardts Verfahren die Grundtöne aus der Obertonreihe ableitet, ergeben sich erwartungsgemäß für den Dur-Dreiklang keine Probleme. Für den Nebendreiklang der VII. Stufe ergibt sich in C-Dur:
Akkordtöne: | h | d | f |
Unisono: | H | D | F |
- Quinte: | E | G | B |
- große Terz: | G | B | Des (Cis) |
+ große Sekunde: | Cis | E | G |
- große Sekunde: | A | C | Es |
| |||
Grundton 3. Grades: | G | ||
Grundtöne 2. Grades: | E, Cis, B | ||
Tabelle 2: Akkordgrundtöne für den verminderten Dreiklang über h nach Terhardt 1982
Somit zeigt sich dieser Akkord wie bei Helmholtz und von Oettingen – im Sprachgebrauch der Funktionstheorie – als verkürzter Dominantseptakkord, was aufgrund seiner Zusammensetzung aus dem 5., 6. und 7. Teilton der Partialtonreihe kaum erstaunt.
Dass sich der Mollakkord nicht aus der Obertonreihe herleiten lässt, ist für Terhardt so selbstverständlich, dass er dies nicht weiter ausführt. Vermutlich teilt er gegen die häufige Erklärung des Mollakkords als 10., 12. und 15. Partial die Vorbehalte Richard Parncutts, der in seinen Publikationen eng an Terhardt anschließt: Erstens müsste nach dieser Argumentation der verminderte Dreiklang konsonanter sein als der Molldreiklang. Zweitens ist der 10. Partial nicht oktavgleich mit dem ersten Partial; also lässt sich der tiefste Ton der Terzschichtung nicht als Grundton herleiten. Drittens sind die Partiale über dem zehnten in ›typischen komplexen Tönen‹ (also typischen musikalischen Klängen) nicht mehr hörbar.[57]
Terhardt erhebt den Anspruch, seine Ergebnisse bewiesen, Molldreiklänge seien eben nicht in demselben Maße ›natürlich‹ und als Bezugssystem geeignet wie Durdreiklänge. Ihre Vertreterfunktion für die Durdreiklänge zeige sich umso deutlicher, als beispielsweise C-Dur und a-Moll die gleichen Grundtöne C, F, D, A besäßen, wenn auch in anderer Rangfolge.[58]
In beiden Fällen ergibt sich für die Grundtonbestimmung:
Akkordtöne: | a | c | e |
Unisono: | A | C | E |
- Quinte: | D | F | A |
- große Terz: | F | As | C |
+ große Sekunde: | H | D | Fis |
- große Sekunde: | G | B | D |
| |||
Grundton 3. Grades: | D | ||
Grundtöne 2. Grades: | A, F, C | ||
Tabelle 3: Akkordgrundtöne für a-Moll nach Terhardt 1982
Doch gerade mit diesem Vorgehen leitet Terhardt den Molldreiklang aus der Obertonreihe ab. Besteht der verminderte Akkord in seinem Modell aus dem 5., 6. und 7. Teilton der Partialtonreihe, so der Mollakkord aus der 6., 7. und 9. ›Harmonischen‹. Während ein Durakkord, dessen Töne im Verhältnis 4:5:6 intoniert werden, genau der reinen Stimmung entspricht, ist die Folge eines im Verhältnis 6:7:9 (statt 10:12:15) intonierten Mollakkords ein Dreiklang »out of tune«.[59]
Zwei weitere »qualitative Zusatzkriterien« ›retten‹ den Grundton a jedoch für a-Moll. Zum einen herrsche beim Gewicht der Grundtöne ein Unterschied:
(5) Die Zeile, in welcher ein Grundtonkandidat in der Tabelle erscheint, kennzeichnet, wenn auch mit einiger Unsicherheit, dessen relatives Gewicht. Je weiter unten er steht, umso geringer ist sein Gewicht einzuschätzen.[60]
Des weiteren leitet Terhardt aus dem dominanten Spektralbereich von etwa 500 bis 1500 Hz und der Prämisse, dass mindestens die ersten beiden Partiale jedes Akkordtons zur Grundtonbestimmung beitragen, ab, dass »die Grundtonfrequenz des tiefsten, noch für die Grundtonbildung sinnvollen Akkordtones bei ungefähr 1/2 bis 1/3 der Untergrenze des dominanten Spektralbereichs liegen dürfte, also bei ungefähr 150 bis 200 Hz«.[61] Daraus folgt:
(4) Akkordtöne, die im Bereich des f bzw. darunter liegen, tragen mit vermindertem Gewicht oder überhaupt nicht zu Grundtonbildung bei. Sie können deshalb im Bestimmungsschema umso eher unberücksichtigt bleiben, je tiefer sie darunter liegen. Im Zweifelsfalle werden sie in das Verfahren einbezogen, wobei jedoch den aus ihnen abgeleiteten Grundtonkandidaten ein geringeres Gewicht zugemessen wird als den übrigen.[62]
Da Terhardt hier überraschend nur noch die ersten beiden Partiale jedes Akkordtones zur Grundtonbestimmung verwendet, stellt sich die Frage, warum er bei der Grundtonbestimmung der Einzeltöne jeweils die ersten zehn Partiale heranzieht. Denn dadurch bekommt der ›virtuelle Grundton‹ mehr für die Grundtonbestimmung wichtige Partiale zugesprochen als der reale Basston.
Doch was zunächst den Basston zu schwächen scheint, stärkt ihn, da »die selbständige Funktion des Baßtones darin bestehen [kann], von den miteinander konkurrierenden Grundtönen eines darüberliegenden Akkords einen bestimmten zu ›bestätigen‹.«[63] Die gestärkte Position des Basses lässt sich auch an der ›Carole-King‹-Kadenz verdeutlichen. Auf den ersten Blick scheint bezüglich der Grundtonbestimmung kein Unterschied zwischen den zwei folgenden Akkorden zu existieren:
Beispiel 11: Grundtonbestimmung des ›Carole-King‹-Akkords nach Terhardt
In beiden Fällen ergibt sich für die Grundtonbestimmung:
Akkordtöne: | f | g | a | c |
Unisono: | F | G | A | C |
- Quinte: | B | C | D | F |
- große Terz: | Des | Es | F | As |
+ große Sekunde | G | A | H | D |
- große Sekunde | Es | F | G | B |
| ||||
Grundton 4. Grades: | F | |||
Grundton 3. Grades: | G | |||
Grundtöne 2. Grades: | C, Es, A, D, B | |||
Tabelle 4: Grundtöne des ›Carole-King‹-Akkords nach Terhardt 1982
Terhardts Verfahren scheint zunächst wie Hindemiths Modell f als Grundton beider Akkorde zu postulieren. Doch nun bestätigt der Basston G den Vorrang des Grundtons dritten Grades gegenüber dem Grundton vierten Grades als Akkordgrundton. Wie der Basston einen von mehreren möglichen Grundtönen der oberen Töne des Akkordes festlegt, zeigen auch die ›Spinning-Wheel-Akkorde‹:
Akkordtöne: | e | gis | d | g |
| a | g | cis | fis |
Unisono: | E | Gis | D | G |
| A | G | Cis | Fis |
- Quinte: | A | Cis | G | C |
| D | C | Fis | H |
- große Terz: | C | E | B | Es |
| F | Es | A | D |
+ große Sekunde: | Fis | Ais (B) | E | A |
| H | A | Dis (Es) | Gis |
- große Sekunde: | D | Fis | C | F |
| G | F | H | E |
|
|
|
|
|
|
|
|
|
|
Grundtöne 3. Grades: | E, C |
| A, H | ||||||
Grundtöne 2. Grades: | A, Fis, D, B, G |
| D, F, G, Es, Fis | ||||||
Tabelle 5: Akkordgrundtöne der ›Spinning-Wheel-Akkorde‹ nach Terhardt 1982
Als Grundtöne dritten Grades sind die Basstöne hier zugleich Grundtöne der Akkorde.
Nach diesen Beispielen für Dur-Akkorde folgt ein Blick auf den Moll-Akkord der II-V-I-Verbindung. In der Tabelle bezeichnen die Werte ohne Klammer die quintfreie Fassung, die Werte in den Klammern schließen die Quinte ein:
Akkordtöne: | d | c | f | e | (a) |
Unisono: | D | C | F | E | (A) |
- Quinte: | G | F | B | A | (D) |
- große Terz: | B | As | Des | C | (F) |
+ große Sekunde: | E | D | G | Fis | (H) |
- große Sekunde: | C | B | Es | D | (G) |
|
|
| |||
Grundtöne 4. Grades: |
| (D) | |||
Grundtöne 3. Grades: | D, B, C | (G, B, C, F) | |||
Grundtöne 2. Grades: | G, F |
| |||
Tabelle 6: Akkordgrundtöne für den Akkord der II. Stufe in der II-V-I-Verbindung nach Terhardt 1982
Während die Form mit Quinte über einen stabilen Grundton (n-1)ten Grades verfügt, besitzt die quintfreie Form drei Grundtöne (n-1)ten Grades, von denen der Basston das d bestätigt.
Im modifizierten Akkord der V. Stufe unterstreicht die hinzugefügte Sexte den potentiellen Grundton a; seine Position als Basston etabliert dennoch g als Grundton:
Akkordtöne: | g | h | f | e | (a) |
Unisono: | G | H | F | E | (A) |
- Quinte: | C | E | B | A | (D) |
- große Terz: | Es | G | Des (Cis) | C | (F) |
+ große Sekunde: | A | Cis | G | Fis | (H) |
- große Sekunde: | F | A | Es | D | (G) |
|
|
| |||
Grundtöne 4. Grades: |
| (G, A) | |||
Grundtöne 3. Grades: | G, A | (F) | |||
Grundtöne 2. Grades: | Es, F, E, Cis |
| |||
Tabelle 7: Akkordgrundtöne für den Akkord der V. Stufe in der II-V-I-Verbindung nach Terhardt 1982
Richard Parncutt
Richard Parncutt gehört zu den wenigen Musikwissenschaftlern, die Terhardts Modell zur Akkordgrundtonbestimmung rezepierten. Allerdings wird auch sein Modell zur Grundtonbestimmung bislang nicht zur Musikanalyse verwendet, sondern lediglich in psychoakustischen Arbeiten im Abschnitt zum Stand der Forschung erwähnt oder in Computerprogramme implementiert. So führt Marc Leman in seinem Forschungsbericht über die Bedeutung der ›neuromusicology‹ für die Musikforschung Terhardt 1974 und Parncutt 1988 als Beispiele an, wie die Idee ›virtueller Grundtöne‹ in die Harmonielehre eingeführt werden könnte.[64] Beide Modelle adaptierte Leman auch für seine Theorie der musikalischen Wahrnehmung und entwickelte sie in Computersimulationen weiter.[65] Petri Toivianinen schlägt in seinem Artikel über computergesteuerte Echtzeiterkennung musikalischer Improvisationen eine Implementation von Parncutts Modell vor.[66] Nicola Cufaro Petronis und Matteo Tricaricos Computersimulation zur Wahrnehmung des Quintenzirkels basiert unter anderem auf Parncutts Modell.[67] Schließlich modifizierte Robert Rowe Parncutts Algorithmen für sein Computerprogramm Cypher zur Erkennung von Akkordgrundtönen.[68]
Richard Parncutt kritisiert an Terhardts Modell zur Grundtonbestimmung, es versage bei der Bestimmung des Grundtons im Mollakkord.[69] Terhardt bestimme zwar die möglichen Grundtöne einer Form korrekt, gewichte diese aber nicht. Um diesen Mangel zu beheben, zieht Parncutt eine für Terhardts Modell grundlegende akustische Untersuchung Terhardts und seiner Mitarbeiter zur Bestimmung ›virtueller Tonhöhen‹ in Sinustongemischen heran. Da die Bedeutung eines Partials für die Grundtonbestimmung abnimmt, je höher es in der Obertonreihe steht, gewichtet Parncutt das n-te Partial mit 1/n.[70] Für die ersten zehn Partiale ergeben sich demnach folgende Werte:
Beispiel 12: Gewichtung potentieller Grundtöne nach Parncutt 1988
Da einige Teiltöne in mehreren Oktaven auftreten, summieren sich ihre Werte: für den Grundton und seine Oktaven zu 1 + 1/2 + 1/4 + 1/8 = 15/8, für die Quinte zu 1/3 + 1/6 = 1/2, für die große Terz zu 1/5 + 1/10 = 3/10. Zur besseren Vergleichbarkeit teilt Parncutt diese Werte durch den Wert für den Grundton und erhält so für Terhardts fünf potentielle Grundtöne die folgenden Werte: 1,00 für das Unisono, 0,27 für die Quinte, 0,16 für die große Terz, 0,08 für die große Sekunde aufwärts und 0,06 für die große Sekunde abwärts. Da diese Gewichtungen für die Akkordgrundtonbestimmung zu unhandlich sind, wählt Parncutt ›intuitiv sinnvollere‹ Werte (»intuitively more reasonable set of values«), die er durch Potenzierung mit dem willkürlich (»arbitrary«) gewählten Wert 0,55 erhält: für das Unisono 1,00, für die Quinte 0,48 (= ca. 1/2), für die große Terz 0,36 (= ca. 1/3), für die kleine Septime 0,24 (= ca. 1/4) und für die große Sekunde 0,21 (= ca. 1/5).[71]
Da Parncutt erklärtermaßen die Grundtöne von Molldreiklängen in Terhardts Modell stärken möchte, kann sich ein potentieller Grundton außer auf die fünf von Terhardt postulierten Obertöne auch auf seine Mollterz beziehen. Parncutts Argument erinnert an von Oettingens Prinzip des ›phonischen Obertons‹: Das dritte Partial der Mollterz ist zum siebten Partial des Grundtons oktavgleich, das fünfte Partial der Mollterz zum dritten Partial des Grundtons.[72]
Diese komplizierte Berechnung ist freilich weitgehend irrelevant, da sich das geringe, von Parncutt ohne nähere Begründung auf 0,10 geschätzte[73] Gewicht der Mollterz in den Grundtonbestimmungen kaum auswirkt, wie Parncutts eigene Berechnung für den Grundton des c-Moll-Akkords zeigt:[74]
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 | 1 |
|
| 1 |
|
|
| 1 |
|
|
|
|
r5 | 0,5 |
|
|
|
| 0,5 |
|
| 0,5 |
|
|
|
g3 |
|
|
| 0,33 |
|
|
|
| 0,33 |
|
| 0,33 |
k7 |
|
| 0,25 |
|
| 0,25 |
|
|
| 0,25 |
|
|
g2 |
| 0,2 |
|
|
| 0,2 |
|
|
|
| 0,2 |
|
k3 | 0,1 |
|
|
| 0,1 |
|
|
|
| 0,1 |
|
|
| 1,6 | 0,2 | 0,25 | 1,33 | 0,1 | 0,95 | 0 | 1 | 0,83 | 0,35 | 0,2 | 0,33 |
Tabelle 8: Akkordgrundtöne für den c-Moll-Dreiklang nach Parncutt 1988
Zu den von Terhardt festgestellten Grundtönen dritten und zweiten Grades tritt noch ein weiterer Ton hinzu; die Töne stehen bei Parncutt gemäß ihres Gewichts in der Reihenfolge c, es, g, f und as. Selbst wenn die von Parncutt neu eingeführte Mollterz keine Berücksichtigung fände, hätte c gegenüber dem nächsten potentiellen Grundton immer noch geringfügig mehr Gewicht.
Die Stärkung des Grundtons c erkauft sich Parncutt freilich, indem er jeden die Ton des Akkords mit m1 gewichtet – auch die in der traditionellen Harmonielehre ›akkordfremd‹ genannten Töne. Dadurch verringert sich die Wahrscheinlichkeit für ›verschwiegene‹ Grundtöne, deren Wert, da sie ja nicht als Akkordton auftreten, rein rechnerisch maximal 0,5 + 0,25 + 0,33 + 0,2 + 0,1 = 1,38 betragen kann (da Durterz und Mollterz selten gleichzeitig in einem Akkord auftreten, strenggenommen nur 1,28).
Dies zeigt die Berechnung für den halbverminderten Septakkord über h. Während er nach Terhardt den Grundton g haben müsste, scheint Parncutts Berechnung des halbverminderten Vierklangs den Grundton d wahrscheinlicher zu machen:[75]
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 |
|
| 1 |
|
| 1 |
|
|
| 1 |
| 1 |
r5 |
|
| 0,5 |
| 0,5 |
|
| 0,5 |
|
| 0,5 |
|
g3 |
| 0,33 |
|
|
| 0,33 |
| 0,33 |
|
| 0,33 |
|
k7 |
| 0,25 |
|
| 0,25 |
|
| 0,25 |
|
|
| 0,25 |
g2 | 0,2 |
|
| 0,2 |
|
|
| 0,2 |
| 0,2 |
|
|
k3 |
|
| 0,1 |
|
|
| 0,1 |
| 0,1 |
|
| 0,1 |
| 0,2 | 0,58 | 1,6 | 0,2 | 0,75 | 1,33 | 0,1 | 1,28 | 0,1 | 1,2 | 0,83 | 1,35 |
Tabelle 9: Akkordgrundtöne für den halbverminderten Septakkord über h nach Parncutt 1988
Um zwischen mehreren potentiellen Grundtönen zu entscheiden, führt Parncutt Zusatzkriterien ein. Er unterscheidet zwischen ›root supports‹, den in den Bestimmungstabellen verwendeten Akkordtönen Grundton, Quinte, große Terz, kleine Septime, große None und kleiner Terz, und ›detractors‹, den hinzugefügten Akkordtönen kleine Sekunde, Quarte, Tritonus, große und kleine Sexte sowie große Septime. Der Akkord ist stabiler, wenn eine starke ›root support‹ (Grundton, große Terz, Quinte) im Bass liegt und keine schwache (kleine Septime, große None)[76], ein ›detractor‹ kann kein Basston sein. Zudem wird der Akkord eindeutiger, wenn ›detractors‹ über den ›root supports‹ liegen, da sie dann als Teiltöne ab dem elften Partial gehört werden können.[77] Der Ton d kann nun in einem halbverminderten Akkord in Grundstellung genauso wenig Grundton sein wie f, weil der Basston h zu beiden Tönen kein ›root support‹, sondern ein ›detractor‹ ist. Dagegen ist h ein ›root support‹ von a, als None jedoch nur ein sehr schwacher, weshalb im Ausschlussverfahren nur g und h als potentielle Grundtöne übrig bleiben.[78]
Parncutts Gewichtung der potentiellen Akkordgrundtöne führt zumindest im ersten Schritt zu ähnlichen Ergebnissen wie Hindemiths Theorie: Tritt im Akkord eine Quinte oder Quarte auf, so hat der Intervallgrundton mindestens den Wert 1,5 (1 für den Grundton und 0,5 für die Quinte); eine große Terz bzw. kleine Sexte bekommt mindestens den Wert 1,33 zugewiesen (1 für den Grundton und 0,33 für die Terz). Zu noch bemerkenswerteren Ergebnissen als bei einer einzelnen Quinte führt die Grundtonbestimmung eines Akkordes, wenn der zu bestimmende Akkord einen ganzen Dreiklang enthält. So verhält es sich bei der ›Carole-King-Kadenz‹, wo für Parncutt wie für Hindemith nun das f1 eindeutig Grundton wäre (2,03) und sich der Basston G (1,45) mit seiner Unterquinte c1 (1,5) und a (1,35) denselben Rang teilen müsste:
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 | 1 |
|
|
|
| 1 |
| 1 |
| 1 |
|
|
r5 | 0,5 |
| 0,5 |
|
| 0,5 |
|
|
|
| 0,5 |
|
g3 |
| 0,33 |
| 0,33 |
| 0,33 |
|
| 0,33 |
|
|
|
k7 |
|
| 0,25 |
|
|
|
| 0,25 |
| 0,25 |
| 0,25 |
g2 |
|
|
| 0,2 |
| 0,2 |
| 0,2 |
|
| 0,2 |
|
k3 |
|
| 0,1 |
| 0,1 |
| 0,1 |
|
| 0,1 |
|
|
| 1,5 | 0,33 | 0,85 | 0,53 | 0,1 | 2,03 | 0,1 | 1,45 | 0,33 | 1,35 | 0,7 | 0,25 |
Tabelle 10: Akkordgrundtöne für den ›Carole-King‹-Akkord G-a-c1-f1 nach Parncutt 1988
Für diesen Akkord räumt Parncutt allerdings die Möglichkeit einer bassbezogenen Deutung als V. Stufe mit G als Grundton ein:
An example of a chord whose bass lies an M2 above the root is a dominant eleventh chord with missing third and fifth: a IV triad on a V bass. Because the M2 is such a weak root support, however, the root of this chord is ambiguous; it may be regarded as either IV or V.[79]
Parncutt schlägt damit wie Terhardt die Bestätigung eines potentiellen Grundtons durch den realen Basston vor. Doch bleibt unklar, welche Bedeutung die Akkordtongewichtungen überhaupt haben, wenn – wie im vorliegenden Beispiel – die Lage des G als Basston diesen Ton bereits als Grundton des Akkordes definiert, obwohl sein Wert um 0,58 geringer ist als der Wert von f1. Zudem hält Parncutt an der Möglichkeit fest, der Akkord könne tatsächlich als Subdominante mit None im Bass gehört werden.
Betrachten wir nun die vierstimmige Fassung der II-V-I-Verbindung:
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 | 1 |
| 1 |
| 1 | 1 |
|
|
|
|
|
|
r5 |
|
|
|
|
| 0,5 |
| 0,5 |
| 0,5 | 0,5 |
|
g3 | 0,33 | 0,33 |
|
|
|
|
|
| 0,33 |
| 0,33 |
|
k7 |
|
| 0,25 |
| 0,25 |
| 0,25 | 0,25 |
|
|
|
|
g2 | 0,2 |
| 0,2 | 0,2 |
|
|
|
|
|
| 0,2 |
|
k3 |
|
|
|
|
|
| 0,1 |
| 0,1 |
| 0,1 | 0,1 |
| 1,53 | 0,33 | 1,45 | 0,2 | 1,25 | 1,5 | 0,35 | 0,75 | 0,34 | 0,5 | 1,03 | 0,1 |
Tabelle 11: Akkordgrundtöne für den Akkord der II. Stufe der II-V-I-Verbindung nach Parncutt 1988
Der korrekte Grundton d liegt mit 1,45 etwa gleich auf mit c1 (1,53) und Hindemiths Grundton f1 (1,5); er wird durch seine Lage als Basston bestätigt, da d ein ›detractor‹ zu f und nur ein schwacher ›root support‹ zu c ist.
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 |
|
|
|
| 1 | 1 |
| 1 |
|
|
| 1 |
r5 | 0,5 |
|
|
| 0,5 |
|
|
|
| 0,5 | 0,5 |
|
g3 | 0,33 | 0,33 |
| 0,33 |
|
|
| 0,33 |
|
|
|
|
k7 |
| 0,25 |
|
|
|
| 0,25 | 0,25 |
| 0,25 |
|
|
g2 |
|
| 0,2 | 0,2 |
| 0,2 |
|
|
| 0,2 |
|
|
k3 |
| 0,1 | 0,1 |
| 0,1 |
|
|
| 0,1 |
|
|
|
| 0,83 | 0,68 | 0,3 | 0,53 | 1,6 | 1,2 | 0,25 | 1,58 | 0,1 | 0,95 | 0,5 | 1 |
Tabelle 12: Akkordgrundtöne für den Akkord der V. Stufe der II-V-I-Verbindung nach Parncutt 1988
Hier hat der tatsächliche Grundton g (1,58) den gleichen Wert, wie der Grundton nach Hindemith e (1,6). Parncutt gibt im Gegensatz zu allen anderen möglichen Tönen nicht an, ob sie einen starken oder schwachen ›root support‹ darstellt. Wäre sie nur ein schwacher, so müsste in einem Mollsextakkord in der Regel der Basston auch als Grundton angesehen werden. In unserem Beispielakkord könnte somit auch e der Grundton sein. Für den Grundton g spricht freilich nicht nur seine Lage als Basston, sondern auch, dass e2 als hinzugefügte Sexte und somit als ›detractor‹ über den Akkordtönen Grundton, Terz und Septime liegt.
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 | 1 |
| 1 |
| 1 |
|
|
|
|
|
| 1 |
r5 |
|
|
|
| 0,5 | 0,5 |
| 0,5 |
| 0,5 |
|
|
g3 | 0,33 |
|
|
|
|
|
| 0,33 | 0,33 |
| 0,33 |
|
k7 |
| 0,25 | 0,25 |
| 0,25 |
| 0,25 |
|
|
|
|
|
g2 | 0,2 |
| 0,2 |
|
|
|
|
|
| 0,2 | 0,2 |
|
k3 |
| 0,1 |
|
|
|
|
|
| 0,1 | 0,1 |
| 0,1 |
| 1,53 | 0,35 | 1,45 | 0 | 1,75 | 0,5 | 0,25 | 0,83 | 0,43 | 0,8 | 0,53 | 1,1 |
Tabelle 13: Akkordgrundtöne für den Akkord der I. Stufe der II-V-I-Verbindung nach Parncutt 1988
In diesem Fall liegt der Grundton c (1,53) nicht nur etwa gleichauf mit d (1,45), sondern Hindemiths Grundton e hat einen deutlich höheren Wert (1,75). Allerdings ist e ein ›detractor‹ zu c und nur ein schwacher ›root support‹ zu d.
Auch in der ›Spinning-Wheel-Akkordfolge‹, in der jeweils zu einem (im Sinne der Funktionstheorie) ›verkürzten‹ Septakkord ein ›harmoniefremder‹ Ton hinzutritt, führt das große Gewicht der Quarte in den beiden Oberstimmen für die höchste Stimme zu ähnlich hohen Werten wie für die Basstöne. Der zweite Akkord muss hier nicht diskutiert werden, da er eine Transposition in anderer Lage des bereits besprochenen Akkords der V. Stufe aus der II-V-I-Verbindung ist. Daher nur ein Blick auf den ersten Akkord:
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 |
|
| 1 |
| 1 |
|
| 1 | 1 |
|
|
|
r5 | 0,5 | 0,5 |
|
|
|
|
| 0,5 |
| 0,5 |
|
|
g3 | 0,33 |
|
| 0,33 | 0,33 |
|
|
|
|
| 0,33 |
|
k7 |
|
|
|
| 0,25 |
| 0,25 |
|
| 0,25 | 0,25 |
|
g2 | 0,2 |
| 0,2 |
|
| 0,2 | 0,2 |
|
|
|
|
|
k3 |
| 0,1 |
|
| 0,1 | 0,1 |
|
|
|
|
| 0,1 |
| 1,03 | 0,6 | 1,2 | 0,33 | 1,68 | 0,3 | 0,45 | 1,5 | 1 | 0,75 | 0,58 | 0,1 |
Tabelle 14: Akkordgrundtöne für den ersten ›Spinning-Wheel-Akkord‹ nach Parncutt 1988
Der höhere Wert für den Basston e im ersten Akkord verringert sich, wenn man den Wert für die ›Mollterz‹ e-g (0,1) abzieht, auf 1,58 gegenüber 1,5 für den ›Quartgrundton‹ g. Wieder ist der Grundton also nur durch seine Lage als Basston gegenüber dem ›detractor‹ g als höchstem Akkordton bestimmt.[80]
Einige Jahre später legte Parncutt eine überarbeitete Fassung seines Modells vor. Zunächst nahm er eine neue Gewichtung der ›Grundtonkandidaten‹ vor. Aufgrund eigener experimenteller Ergebnisse[81] kam er zu dem Schluss, er hätte die Werte für die weniger wichtigen Intervalle (k7, g2) im Vergleich zu den wichtigen Intervallen (r1 und r5) zu hoch angesetzt. Er passte die Werte entsprechend an und multiplizierte anschließend mit 10, da sich mit geraden Zahlen besser rechnen ließe, als mit den Nachkommastellen in der früheren Fassung des Modells. Dadurch erhielt er folgende Werte: 10 (r1), 5 (r5), 3 (g3), 2 (k7) und 1 (g2); die Bewertung der Mollterz ließ er fallen.[82] Aus diesen Änderungen folgt also zunächst eine weitere Stärkung des Quintintervalls.
Diesen Effekt gleicht Parncutt aus, indem er als zweiten Faktor der Grundtonbestimmung das ›voicing‹ des Akkords berücksichtigt, worunter er hier allerdings nur versteht, welcher Akkordton im Bass liegt, zu dessen Gewicht er den Wert 20 addiert.[83] Dieser Faktor ersetzt also die Unterscheidung zwischen ›root support‹ und ›detractor‹.
Um dem tonalen Kontext Rechnung zu tragen, gewichtet Parncutt ferner die Töne der chromatischen Skala nach ihrer funktionalen Bedeutung für die Dur- bzw. Molltonalität (›prevailing tonality‹):[84]
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Dur | I |
| II |
| III | IV |
| V |
| VI |
| VII |
Gewicht | 33 | 0 | 10 | 1 | 17 | 15 | 2 | 24 | 1 | 11 | 0 | 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Moll | I |
| II | III |
| IV |
| V | VI |
| VII |
|
Gewicht | 28 | 3 | 9 | 21 | 3 | 9 | 2 | 17 | 12 | 3 | 8 | 6 |
Tabelle 15: Gewichtung der ›prevailing tonality‹ nach Parncutt 1997
Die Stimmführung als vierten Faktor deutet Parncutt nur kurz an, integriert sie aber nicht in sein Modell.[85]
In der neuen Fassung des Modells ist durch die starke Gewichtung der V. Stufe der Durtonleiter im Rahmen der ›prevailing tonality‹ einerseits, die starke Gewichtung des Basstons im Rahmen des ›voicing‹ andererseits der Basston des ›Carole-King-Akkords‹ als Grundton ›gerettet‹.
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 | 10 |
|
|
|
| 10 |
| 10 |
| 10 |
|
|
r5 | 5 |
| 5 |
|
| 5 |
|
|
|
| 5 |
|
g3 |
| 3 |
| 3 |
| 3 |
|
| 3 |
|
|
|
k7 |
|
| 2 |
|
|
|
| 2 |
| 5 |
| 2 |
g2 |
|
|
| 1 |
| 1 |
| 1 |
|
| 1 |
|
pt | 33 |
| 10 | 1 | 17 | 15 | 2 | 24 | 1 | 11 |
| 5 |
| 48 | 3 | 17 | 5 | 17 | 34 | 2 | 37 | 4 | 26 | 6 | 7 |
Tabelle 16: Akkordgrundtöne für den ›Carole-King-Akkord‹ nach Parncutt 1997
Durch die zusätzliche Gewichtung des Basstons um den Wert 20 erhält g somit den Wert 57 gegenüber dem nächstgrößten Wert 47 für c. Knapper fällt das Ergebnis aus, wenn bei den gleichen Akkordtönen f im Bass liegt (54 für f gegen 48 für c). Da Parncutt erklärt, nur Werte, die um 4 oder weniger differierten, sollten als gleich angesehen werden[86], ist hier die Grundtonbestimmung noch eindeutig. Genau diese Differenz erreicht aber die Grundtonbestimmung für die II. Stufe der II-V-I-Verbindung:
| c | cis/des | d | dis/es | e | f | fis/ges | g | gis/as | a | ais/b | h |
r1 | 10 |
| 10 |
| 10 | 10 |
|
|
|
|
|
|
r5 |
|
|
|
|
| 5 |
| 5 |
| 5 | 5 |
|
g3 | 3 | 3 |
|
|
|
|
|
| 3 |
| 3 |
|
k7 |
|
| 2 |
| 2 |
| 2 | 2 |
|
|
|
|
g2 | 1 |
| 1 | 1 |
|
|
|
|
|
| 1 |
|
pt | 33 |
| 10 | 1 | 17 | 15 | 2 | 24 | 1 | 11 |
| 5 |
| 47 | 3 | 23 | 2 | 29 | 30 | 4 | 31 | 4 | 16 | 8 | 5 |
Tabelle 17: Akkordgrundtöne für den Akkord der II. Stufe der II-V-I-Verbindung nach Parncutt 1997
Dem Wert 43 für den Basston d steht nun der Wert 47 für den Ton c gegenüber. Betrüge die Differenz hier nicht 4 sondern 5, stünde c als Grundton fest.
Anhand der eröffnenden Akkordfolge des Titels A hard days night von den Beatles lässt sich zeigen, dass nach Parncutts revidiertem Modell sogar reine Durdreiklänge unbestimmbar werden können:
Beispiel 13: Anfangsakkorde von A hard days night von den Beatles
Nehmen wir als Grundtonart G-Dur an, welche die Beatles später durch Kadenzierungen bestätigen, so liegt hier mit dem vierten Akkord eine Doppel-Subdominante vor, deren Basston nach diesem Modell nicht zwingend der Grundton ist:
| g | gis/as | a | ais/b | h | c | cis/des | d | dis/es | e | f | fis/ges |
r1 |
|
| 10 |
|
| 10 |
|
|
|
| 10 |
|
r5 |
|
|
| 5 |
|
|
| 5 |
|
| 5 |
|
g3 |
| 3 |
|
|
|
| 3 |
|
|
| 3 |
|
k7 | 2 |
|
|
| 2 |
|
| 2 |
|
|
|
|
g2 | 1 |
|
| 1 |
|
|
|
| 1 |
|
|
|
pt | 33 |
| 10 | 1 | 17 | 15 | 2 | 24 | 1 | 11 |
| 5 |
| 36 | 3 | 20 | 7 | 19 | 25 | 5 | 31 | 2 | 11 | 18 | 5 |
Tabelle 18: Akkordgrundtöne für die Doppelsubdominante in G-Dur nach Parncutt 1997
Die Differenz zwischen den Werten 38 für den Basston f und 36 für den Grundton der Tonart g beträgt nur 2, da der untersuchte Dreiklang über einem Ton errichtet wird, dem nach der ›prevailing tonality‹ kein eigener Wert zukommt. Das Beatles-Beispiel verweist zudem auf ein weiteres Problem: Der Melodieton f1 lässt sich als kleine Septime der Blues-Skala interpretieren, da das Ende dieser Melodie außerdem durch einen Wechsel von kleiner und großer Terz gekennzeichnet ist. Für die Bluestonleiter gelten die von Parncutt postulierten Werte für Dur- und Moll-Tonleiter wohl nur bedingt (Genauso müssten für die Kirchentonarten im Rahmen der ›prevailing tonality‹ eigene Gewichtungen bestimmt werden). Die ›Spinning-Wheel-Akkorde‹ lassen sich mit dieser Methode ebenfalls schwer analysieren, denn es ist unklar welche Tonart ist dieser Quintenverbindung zugrundeliegt. Nach dem G7/13-Akkord beginnt die Akkordfolge von neuem. Ist G-Dur die Tonika oder selbst ein auflösungsbedürftiger Akkord, der sich auf eine verschwiegene Tonika C-Dur bezieht? Auch der Refrain von Spinning Wheel mit der Mixturfolge B-As-Ges-F gibt darüber keinen Aufschluss. Interessant ist allerdings, dass durch die ›prevailing tonality‹ zudem die Grundtöne des ersten und dritten bzw. des zweiten und vierten ›Spinning-Wheel-Akkords‹ unterschiedliche Gewichtungen erhielten. Daher erscheint auch fraglich, ob mit einer Weiterentwicklung dieses Modells die harmonischen Prozeduren ›tonaler Modernisten‹ wie Debussy und Stravinskij oder die Harmonik des Bebop erklärt werden können, wie Parncutt es für möglich hält.[87]
Llorenç Balsach
Der Komponist Llorenç Balsach entwickelte sein Modell zur Akkordgrundtonbestimmung ursprünglich unabhängig von Terhardt und Parncutt[88], berief sich aber in seiner späteren englischsprachigen Fassung der Theorie auf die beiden Psychoakustiker.[89] Auf diese beiden und Balsach bezieht sich wiederum das im Folgenden noch diskutierte Modell von Hofmann-Engl.[90] Außerdem implementierten Carreras, Leman und Lesaffre das im Vergleich zu Terhardts und Parncutts Ansätzen leichter handhabbare Modell in ihr Programm zur computergesteuerten Transkription von Akkorden.[91]
Im Gegensatz zu Terhardt und Parncutt stützt sich Balsach in seine Theorie nur auf die ersten sieben Partiale der Obertonreihe. Wie Terhardt und Parncutt berücksichtigt er das ›voicing‹ der Akkorde zunächst nicht, da sich aus gleichen Tönen gebildete Akkorde nur in ihrem Konsonanzgrad, nicht jedoch in ihrer Funktion unterscheiden. Seiner Theorie zufolge setzten sich alle Akkorde aus ›convergent chords‹ zusammen, Ausschnitte aus einem Durakkord mit kleiner Septime.[92]
Beispiel 14: ›convergent chords‹ nach Balsach 1994
Die großen Buchstaben bedeuten bei Balsach, dass in diesem Akkord im Gegensatz zu einem Akkord mit kleinem Buchstaben die große Terz zum Grundton enthalten ist, das ° bezeichnet die kleine Septime, durchgestrichene Buchstaben verweisen auf den fehlenden Grundton.
93,3% aller möglichen Akkorde mit bis zu fünf Tönen lassen sich Balsach zufolge als Zusammensetzung aus zwei ›convergent chords‹ erklären, diese Akkorde verfügen demnach über zwei Grundtöne.[93] Balsach billigt Quinten aufgrund ihres starken Verschmelzungsgrads eine viel geringere Bedeutung für die Akkordgrundtonbestimmung zu als großen Terzen und kleinen Septimen.[94] Wie in der Diskussion früherer Modelle bereits gezeigt, führt eine Überbetonung der Bedeutung der Quinte tatsächlich zu offensichtlichen Fehlern in der Grundtonbestimmung. Balsach zieht aus dieser Überlegung daher auch den Schluss, dass c Grundton des a-Molldreiklangs ist, da in seinem Modell die große Terz c-e mehr Gewicht hat als die Quinte a-e. Die Funktion des c als Akkordgrundton ist jedoch unabhängig davon, dass ein a-Molldreiklang mit a im Bass konsonanter klingt als der gleiche Akkord in einer anderen Stellung: Auch die Funktionstheorie sehe a nicht als Grundton an, da dieser Akkord sonst eine Dominante zu D-Dur wäre.[95]
Da Balsach nicht nur Grundtonpaare zulässt, sondern für komplexe Akkorde wegen ihrer Zusammensetzung aus ›convergent chords‹ zwei gleichzeitige Grundtöne als Norm begreift, erhält man nach seinem Modell für den ›Carole-King-Akkord‹ die Grundtöne G und f:
Beispiel 15: ›Carole-King-Akkord‹ nach Balsach 1994
In der II-V-I-Verbindung wird erwartungsgemäß f zum Grundton des Mollakkordes. Erstaunlich ist dagegen, dass der Basston nach diesem Modell zur Septime eines e-Akkordes erklärt wird:[96]
Beispiel 16: II-V-I-Verbindung nach Balsach 1994
Durch die fehlenden Töne fällt für die V. und I. Stufe der vierstimmigen Fassung der II-V-I-Verbindung jeweils der zweite Grundton weg, wodurch es zu einem neuen zweiten Grundton kommt. Entgegen der These von der geringen Bedeutung der Quinten für die Grundtonbildung erhält die quintlose II. Stufe gleich zwei neue Grundtöne.[97]
Ludger Hofmann-Engl
Ludger Hofmann-Engl, dessen Modell ebenfalls auf dem Konzept des ›virtuellen Grundtons‹ basiert, versucht seinen Anspruch, das von ihm entwickelte Modell könne auch Musik des 20. Jahrhunderts erklären, mit der Analyse dreier stilistisch höchst unterschiedlicher Klavierkompositionen unter Beweis zu stellen: Schönbergs op. 19,2, ein Stück aus Bartoks Mikrokosmos sowie Szymanowskis Etude op. 33,6.
Im Gegensatz zu Hindemiths offensichtlich falschem Ansatz erscheint Hofmann-Engl Terhardts Modell vielversprechend. Parncutts Weiterentwicklung habe den Fehler, dass sie Terhardts Nachweis von d als Grundton von a-Moll negiere. Denn, wie Balsach nachweise, sei a nicht Grundton von a-Moll, da dieser Akkord nicht Dominante zu D-Dur/d-Moll sein könne. Der Fehler von Balsachs Modell wiederum bestehe darin, dass er keine höheren Teiltöne als den siebten einbeziehe und daher viele Akkorde nicht erklären könne.[98] Um den Durakkord mit großer Septime (z.B. c-e-g-h) in sein System zu bekommen, geht Hofmann-Engl daher bis zum 15. Partial. Dabei schließt er die Teiltöne 11 und 13 aus, da diese Grundtöne außerhalb der temperierten Stimmung produzieren würden. Bei Berechnungen für mikrotonale Kompositionen seien sie hingegen einzubeziehen.
Hofmann-Engl gewichtet die von ihm zur Berechnung herangezogenen Intervallen Prime, reine Quinte, große Terz, kleine Septime, große None und große Septime mit einer Formel, die er eigenen Angaben nach aus eigenen Voruntersuchungen und in Anlehnung an Carl Stumpfs ›Verschmelzungsgrad‹ gewonnen habe:
Abb. 1: Intervallgewicht nach Hofmann-Engl 2004
Dabei ist ›w‹ das Gewicht des jeweiligen Intervalls, ›c‹ ist eine Konstante = 6 Hh (Hofmann-Engl setzt hier die Maßeinheit ›Helmholtz‹), b eine Variable mit 0 für die Oktave, 1 für die Quinte, 2 für die große Terz, 3 für die kleine Septime, 4 für die große Sekunde, 5 für die große Septime und 6 für alle anderen Intervalle. Durch Einsetzen dieser Werte in die Formel erhält er die Ergebnisse w0 = 6,00, w1 = 5,83, w2 = 5,33, w3 = 4,50, w4 = 3,33, w5 = 1,83 und w6 = 0. Ähnlich wie Terhardt und Parncutt, die postulierten, dem Basston komme als Grundtonkandidaten ein höheres Gewicht zu, gewichtet auch Hofmann-Engl die Lage eines Tones im Akkord. Er bezieht dabei aber nicht nur den Basston, sondern auch die übrigen Töne mit ein, je tiefer ein Akkordton, desto höher sein Gewicht:
Abb. 2: Tongewicht nach Lage im Akkord nach Hofmann-Engl 2004
Hier ist wp das Gewicht des Grundtonkandidaten in Bezug auf die Position ›i‹ im Akkord, wobei in einem Dreiklang der Basston den Wert i = 1, der nächst höhere Ton den Wert i = 2 hat. Wie Terhardt und Parcutt stellt Hofmann-Engl nun die ›Subharmonischen‹ für jeden Akkordton fest. Darüber hinaus gewichtet er jeden Grundtonkandidaten indem er ihn zu jedem Akkordton als ›Subharmonischen‹ wichtet und diesen Wert mit dem Gewicht der Lage im Akkord multipliziert, diese Ergebnisse addiert und schließlich durch die Zahl der Akkordtöne teilt:
Abb. 3: Formel für Grundtongewichtung nach Hofmann-Engl 2004
Für einen C-Durdreiklang in Grundstellung ergibt sich nach einer solchen Berechnung wie zu erwarten ein stabiler Grundton c mit einem Wert von 4,37 Hh, der nächstgrößte Wert beträgt für f nur 3,01. Wie bereits erwähnt, schließt dieses Modell aber in der Bewertung des Molldreiklangs eng an Terhardt an. Zunächst sind wie bei Terhardt und Parncutt die ›Subharmonischen‹ zu bestimmen:
Subharmonische | Gewicht | a (Ton 1) | c (Ton 2) | e (Ton 3) |
r1 | 6,00 | a | c | e |
r5 | 5,83 | d | f | a |
g3 | 5,33 | f | gis/as | c |
k7 | 4,50 | h | d | fis/ges |
g2 | 3,33 | g | ais/b | d |
g7 | 1,83 | ais/b | cis/des | f |
Tabelle 19: Akkordgrundtöne für den a-Moll-Dreiklang nach Hofmann-Engl 2004
Diese Werte werden nun in die Formel eingesetzt, für den ›Grundtonkandidaten‹ a ergibt sich dabei:
Abb. 4: Gewicht für den ›Grundtonkandidaten‹ a für den a-Moll-Dreiklang nach Hofmann-Engl 2004
Wie in Terhardts Modell wird aber auch hier der Molldreiklang als 6., 7. und 9. Partial der Obertonreihe interpretiert:
Abb. 5: Gewicht für den ›Grundtonkandidaten‹ d für den a-Moll-Dreiklang nach Hofmann-Engl 2004
Die Interpretation des a-Molldreiklang als 10., 12. und 15. Partial über f wird allerdings durch einen ähnlich hohen Wert gestützt:
Abb. 6: Gewicht für den ›Grundtonkandidaten‹ f für den a-Moll-Dreiklang nach Hofmann-Engl 2004
Außer dem bereits erwähnten Argument Balsachs, a-Moll könne keine Dominante zu D-Dur sein, führt Hofmann-Engl für die Richtigkeit seiner Grundtonbestimmung an, dass vor allem Mollkompositionen des Barock meist mit dem entsprechenden Durakkord schlössen.[99] Freilich ließe sich aus dieser Überlegung mit gleichem Recht ableiten, in Schlüssen von barocken Formteilen könne der Mollakkord mit einer zusätzlichen Unterquinte unterlegt werden, ohne dass dies den Hörer störe.
Hofmann-Engl betont, obwohl sein Modell in keinem Konflikt zur traditionellen Harmonielehre stehe, kämen dessen eigentliche Stärken erst in der Analyse nicht traditioneller Akkorde zum Tragen. Doch bevor diesem Modell in Bezug auf ›atonale‹ Musik Glauben geschenkt wird, sollte es sich zunächst am ›Carole-King-Akkord‹ bewähren:
Subharmonische | Gewicht | G (Ton 1) | a (Ton 2) | c1 (Ton 3) | f1 (Ton 4) |
r1 | 6,00 | g | a | c | f |
r5 | 5,83 | c | d | f | ais/b |
g3 | 5,33 | dis/es | f | gis/as | cis/des |
k7 | 4,50 | a | h | d | g |
g2 | 3,33 | f | g | ais/b | dis/es |
g7 | 1,83 | gis/as | ais/b | cis/des | fis/ges |
Tabelle 20: Akkordgrundtöne für den ›Carole-King-Akkord‹ nach Hofmann-Engl 2004
Für den zu erwartenden Grundton g ergibt sich:
Abb. 7: Gewicht für den ›Grundtonkandidaten‹ g für den ›Carole-King-Akkord‹ nach Hofmann-Engl 2004
Doch auch Hofmann-Engls Modell zieht einmal mehr den Grundton f vor, obwohl dieser Ton als höchster Ton des Akkordes eigentlich eine relativ schwache Position haben müsste:
Abb. 8: Gewicht für den ›Grundtonkandidaten‹ f für den ›Carole-King-Akkord‹ nach Hofmann-Engl 2004
Wieder ist der im Akkord enthaltene F-Durdreiklang der Grund für diese Grundtonbestimmung.
Durch die starke Gewichtung von Durdreiklangstönen sowie Septimen und großen Nonen bzw. Sekunden einerseits, der Basstöne andererseits, führt die Grundtonbestimmung für die ›Spinning-Wheel-Akkorde‹ und die Durakkorde der II-V-I-Verbindung zu keinen Überraschungen. Und wie ebenfalls zu erwarten, ergibt sich für die II. Stufe der vierstimmigen II-V-I-Verbindung als Mollakkord kein eindeutiger Grundton:
| Gewicht | d (Ton 1) | c1 (Ton 2) | f1 (Ton 3) | e2 (Ton 4) |
r1 | 6,00 | d | c | f | e |
-r5 | 5,83 | g | f | ais/b | a |
-g3 | 5,33 | ais/b | gis/as | cis/des | c |
+g2 | 4,50 | e | d | g | fis/ges |
-g2 | 3,33 | c | ais/b | dis/es | d |
+k2 | 1,83 | dis/es | cis/des | fis/ges | f |
Tabelle 21: Akkordgrundtöne für die II. Stufe der II-V-I-Verbindung nach Hofmann-Engl 2004
Abb. 9: Gewicht für die ›Grundtonkandidaten‹ d und c für die II. Stufe der II-V-I-Verbindung nach Hofmann-Engl 2004
Dass hier überhaupt d stärker gewichtet ist als c, liegt an der zu d vorhandenen kleinen Septime und großen None. Ein etwas höheres Gewicht erreicht freilich ein anderer potentieller Grundton, den auch die Anwendung von Balsachs Modell nahelegt:
Abb. 10: Gewicht für den ›Grundtonkandidaten‹ b für die II. Stufe der II-V-I-Verbindung nach Hofmann-Engl 2004
Diskussion
Mit dem ersten Teil der Unterweisung im Tonsatz formulierte Hindemith den Versuch, auch Musik zu analysieren, die außerhalb des Geltungsbereichs von Funktions- oder Stufentheorie liegt. Den gleichen Anspruch erheben auch Balsach und Hofmann-Engl. Dagegen scheinen sich Terhardt und Parncutt auf tonale Musik zu beschränken, wenngleich Parncutt die Möglichkeit einer Erweiterung seiner Theorie zumindest andeutet.
Hindemiths Modell widerspricht der herkömmlichen Deutung eindeutig tonaler Akkorde, wie sie in Pop- und Jazzmusik gebräuchlich sind. Die Theorie Terhardts kommt zu plausibleren Ergebnissen, hat aber Schwierigkeiten, den Grundton des Mollakkords zu bestimmen. Dabei besteht das Problem weniger in der Annahme eines ›verschwiegenen‹ Grundtons, als vielmehr in der Deutung der Mollterz als Naturseptime zum vermeintlichen Grundton, was eindeutig der reinen Stimmung widerspricht. Die von Terhardt vorgenommene Stärkung des realen Basstons versucht dieses Manko zu mildern. Parncutt ›rettet‹ den traditionell angenommenen Grundton des Mollakkords, indem er einerseits wie Hindemith die im Akkord vorhandenen Quinten und Quarten sehr stark gewichtet und andererseits (im Modell von 1988) wie von Oettingen gemeinsame Partialtöne als Begründung für eine Einbeziehung von Mollterzen in die Grundtonbestimmung anführt. Das Problem der Interpretation der Mollterz als Naturseptime zum vermeintlich ›virtuellen Grundton‹ löst Parncutt durch sein Verfahren freilich nicht, sondern verringert es durch die postulierten Zahlenwerte lediglich. Dabei wird nicht deutlich, welche Bedeutung die errechneten Gewichtungen, die laut Parncutt den großen Vorzug gegenüber Terhardt darstellen, für die Grundtonbestimmung tatsächlich haben, da sie durch die Unterscheidung zwischen ›root supports‹ und ›detractors‹ wieder relativiert werden. Diese Tendenzen verstärkt Parncutt in seinem revidierten Modell von 1997 noch, indem er im Akkord enthaltene Quinten noch stärker gewichtet, im Gegenzug allerdings auch den Basston aufwertet. Dabei erscheint die ›prevailing tonality‹ problematisch, weil sie die Dur-Moll-Tonalität voraussetzt.
Während Parncutt versucht, Terhardts Grundtonbestimmung für den Molldreiklang abzumildern, besteht Hofmann-Engl auf der Richtigkeit dieser Deutung. Dennoch tritt in seiner Argumentation das Dilemma dieser Art der Grundtonbestimmung deutlich hervor. Wie Terhardt, Parncutt und Balsach bezieht er durch den Bezug auf den ›virtuellen Grundton‹ den siebten Partialton in sein Modell ein. Obwohl diese vier Theoretiker ihren Modellen sonst eine temperierte Stimmung zugrundelegen, verwenden sie also ein Intervall, welches Rameau, von Oettingen und Hindemith aus ihren Harmoniesystemen ausschlossen[100], da es zu sehr von den Intonationsgewohnheiten der Musik ihrer Zeit abwich. Dabei forderten zumindest von Oettingen und Hindemith ausdrücklich die reine Stimmung; für Rameau stellte sich das Problem der Konsequenzen einer vollständig etablierten gleichschwebend-temperierten Stimmung noch nicht. Hofmann-Engl wiederum nutzt das gleiche Argument, der siebte Partialton sei ›verstimmt‹, um den 11. und 13. Partialton aus seinem Modell auszuschließen, obwohl er andererseits den Bezug auf die Obertonreihe bis zum 15. Partial ausweitet, um die große Septime einbinden zu können. Nun ist die Abweichung der ›Naturseptime‹ 4:7 von der gleichschwebend-temperierten kleinen Septime mit 31,17 cent in der Tat geringer als die Abweichung des Intervalls 8:11 vom gleichschwebend temperierten Tritonus mit 47,68 cent.[101] Dies entspricht aber ziemlich exakt der Abweichung von 48,76 cent zwischen einer reinen Mollterz 5:6 (315,64 cent) gegenüber der von Terhardt und Hofmann-Engl in ihren Modellen vorausgesetzten ›Mollterz‹ 6:7 (266,88 cent). Selbst der Vergleich des Intervalls 6:7 mit der kleinen Terz der temperierten Stimmung ergibt noch eine Differenz von 33,12 cent.
Diese Modelle setzen also einerseits für die Akkorde die gleichschwebend-temperierte Stimmung voraus, beziehen sich aber andererseits mit dem ›virtuellen Grundton‹ auf die [nicht temperierte] Obertonreihe. Fragwürdig ist zudem die Analogie zwischen dem physikalischen Klang aus einzelnen Sinusschwingungen und dem musikalischen Akkord aus komplexen Tönen. Roland Eberlein wendet ein, Akkordgrundtöne könnten schon deshalb keine ›Residualtöne‹ (Synonym zu Terhardts ›virtuellen Grundtönen‹) sein, »weil auch gebrochene Akkorde mit sukzessiv erklingenden, sich nicht überlappenden Tönen einen Grundton besitzen, obwohl sie nachweislich keinen Residualton erzeugen«.[102] Dem könnte freilich entgegen gehalten werden, der Hörer, der gewöhnt sei, in simultan dargebotenen Akkordtönen einen Grundton zu hören, habe auch gelernt, ihn zu gebrochenen Akkorden hinzuzuhören. Bedeutender scheint Eberleins zweiter Einwand:
Zudem ist es wenig sinnvoll, eine Theorie, die erklärt, wie das Gehör verschiedene Teiltöne zu einem Residualton verschmelzen kann, auf die Wahrnehmung von Akkorden anzuwenden, bei denen eben diese Verschmelzung gar nicht stattfindet.[103]
Die Erfahrungen mit der Elektronischen Musik zeigen ebenfalls, dass die Parameter Harmonik und Klang keineswegs ineinander aufgehen. Als Karlheinz Stockhausen in seiner Studie 1 erstmals serielle Verfahren auf die Komposition mit Sinustönen anwandte, verschmolzen die in einem irrationalen Verhältnis zueinander stehenden Töne eben nicht zu neuen, komplexen Klängen, sondern es entstand der Eindruck von aus Sinustönen gebildeten Akkorden.[104]
Doch bereits Terharts Modell zur Bestimmung von virtuellen Tonhöhen kommt bei der Wahrnehmung von Sinustönen zu anderen Ergebnissen als seine späteren musiktheoretischen Postulate. In der Anwendung auf die musikalische Analyse verzichtete Terhardt auf die im ursprünglichen Modell vorgenommenen Gewichtungen der ›Grundtonkandidaten‹, was Parncutt und Hofmann-Engl durch eigene Gewichtungen wieder ergänzten. Allerdings führte Terhardt, bevor er seinen Aufsatz zur Akkordtonbestimmung veröffentlichte, bereits Grundtonbestimmungen mit seinem ursprünglichen Algorithmus durch. Dafür maß er zunächst das Spektrum für einen temperierten C-Dur-Quartsextakkord auf einer elektronischen Orgel mit den Grundfrequenzen 392 Hz (g1), 532,2 Hz (c2) und 659,2 Hz (e2) und berechnete aus den ersten 10 Partialen dieses Spektrums mittels des vollständigen Algorithmus die Grundfrequenz 126,6 Hz bzw. mit einer vereinfachten Fassung 130,7 Hz, was etwa einem c entspricht.[105] In einer späteren Publikation gab er die mit dem gleichen Algorithmus bestimmten Gewichtungen für ›virtuelle Grundtöne‹ der Umkehrungen des A-Dur und a-Molldreiklangs an, wobei er die Ausgangsdaten aus einer Spektralanalyse von Klavierakkorden gewann:[106]
Stimulus | Extracted musical pitches and weights | |||||
A4C#5E5 | A4 | A3 | A2 | D3 | E6 | F2 |
| 1.41 | 1.09 | 0.59 | 0.52 | 0.35 | 0.28 |
C#5E5A5 | A4 | C#4 | C#5 | A3 | A2 | F#3 |
| 0.46 | 0.41 | 0.40 | 0.35 | 0.34 | 0.33 |
E5A5C#6 | A3 | E5 | A4 | E4 | A5 | E3 |
| 0.60 | 0.54 | 0.52 | 0.42 | 0.38 | 0.29 |
A4C5E5 | A4 | A3 | D3 | A4 | F2 | D3[107] |
| 1.06 | 0.79 | 0.47 | 0.43 | 0.30 | 0.26 |
C5E5A5 | A4 | A3 | F3 | C4 | C3 | E5 |
| 0.53 | 0.47 | 0.45 | 0.42 | 0.40 | 0.40 |
E5A5C6 | E4 | A3 | A4 | A5 | E5 | E3 |
| 0.54 | 0.54 | 0.52 | 0.38 | 0.38 | 0.33 |
Tabelle 22: Bestimmung von Akkordgrundtönen nach Terhardt, Stoll und Sewann 1982a
Diese Daten widerlegen, d sei der Grundton von a-Moll. Der Ton erscheint zwar in den Berechnungen für den Mollakkord, aber nur in dessen Grundstellung, und dort findet er sich auch für den nach Terhardt, im Gegensatz zum Mollakkord, ›natürlichen‹ Durdreiklang. Selbst für den Mollakkord in Sextstellung ist nicht, wie mit Helmholtz oder Balsach vermutet werden könnte, c der Grundton, sondern a.
Wie bei allen Verfahren der Gewichtung potentieller Grundtöne bleibt freilich auch hier unklar, was diese Gewichtungen musikalisch bedeuten. Unklar bleibt auch, welchen Einfluss die Gewichte der oktavidentischen ›Grundtonkandidaten‹ auf die Wahrnehmung von Akkordgrundtönen haben. Eine Alternative zu den besprochenen Modellen ist der ursprüngliche Algorithmus von Terhardt aber auch deshalb nicht, weil sich die Werte selbst für den Grundton eines Durdreiklangs durch einfache Transposition bereits ändern.[108] Ein temperierter A-Durdreiklang (a1-cis2-e2) aus Sinustönen kommt auf den Grundton a1 mit dem Gewicht 0,401, ein temperierter B-Durdreiklang (b1-d2-f2) auf den Grundton b1 mit dem Gewicht 0,410. Der Grundton h1 des temperierten H-Durdreiklangs erhält bereits das Gewicht von 0,417. Dies wäre kein Problem, wenn sich die Gewichte nicht derart verschieben würden, dass Transpositionen nicht nur zu anderen Gewichten von Grundtönen, sondern auch zu völlig anderen ›Grundtonkandidaten‹ führen würden: Die II. Stufe der II-V-I-Verbindung mit d als Basston erhält einen Grundton e2 mit dem Gewicht 0,410, gegenüber dem Basston d mit dem Gewicht 0,274. Im um eine Oktave nach oben transponierten Akkord nähern sich die Werte für d1 (0,432) und e3 (0,437) jedoch an. Noch eine Oktave höher liegt zwischen den ›Grundtönen‹ d2 (0,491) und e4 (0,343) der weitere Ton c2 (0,436). Der Grund für diese Verschiebungen sind fehlende empirische Befunde zu ›virtuellen Grundtönen‹ unterhalb von 50 Hz, weshalb Terhardt diese Töne in seinem Algorithmus auch nicht berücksichtigt. Je höher die Teiltöne des Ausgangsmaterials sind, desto mehr Subharmonische können also berücksichtigt werden. Von den 10 Subharmonischen, die Terhardt zumindest seiner Akkordgrundtonbestimmung zugrunde legt, können also nur für Frequenzen oberhalb des 10fachen Werts der unteren Grenze, also von über 500 Hz berücksichtigt werden, dies entspricht etwa Tönen ab h1 (493,9 Hz innerhalb des gleichschwebend-temperierten Systems mit a1 = 440 Hz).[109] Dies bedeutet für das zitierte Beispiel der II. Stufe der II-V-I-Verbindung: Ein Grundton d kann nur als Basston d oder als erste Subharmonische des Basstons D vorkommen, D liegt schon unterhalb der 50 Hz-Grenze. Somit hat der Akkordton c1 auch keine 7. Subharmonische D.
Ausblick
Die Schwächen der vorgestellten Modelle verweisen auf eine generelle Gefahr naturwissenschaftlicher Begründungen in der Musiktheorie. Mit dem Hinweis auf naturwissenschaftliche Erkenntnisse wird dem Hörer vorgeschrieben, wie und was er zu hören hat: So wie die Musiktheorie soll sich auch die musikalische Auffassung nach der Natur richten.[110] Darin aber missachtet dieses Denken Helmholtz’ in der Einleitung zitierte Mahnung, dass in der Musik nicht nur naturwissenschaftliche Prinzipien herrschen, sondern sich viele ästhetische Prinzipien historisch entwickelt haben. So lässt sich naturwissenschaftlich kaum begründen, woher die unterschiedliche Präferenz für IV-V-I oder II-IV-I-Kadenzen in den verschiedenen stilistischen Zusammenhängen der dur-moll-tonalen Musik herrührt, zu der im weiteren Sinne auch die Jazzmusik in ihren überwiegenden Teilen zählt. Auch hören wir in der Regel a als Grundton eines isolierten a-Mollakkordes in Grundstellung, weil wir es so im Rahmen unserer musikalischen Sozialisation gelernt haben. Andererseits möchte ich keinesfalls Ludger Engl-Hofmann absprechen, dass für ihn die Basstöne d und f besser mit a-Moll verschmelzen als ein Basston a.[111] Ebenso mag für Arthur von Oettingen ein plagaler Mollschluss in a-Moll (bzw. ›e-phonisch‹) mit dem phonischen Oberton e im Bass befriedigender gewesen sein als mit dem tonischen Grundton a.[112]
Die Ergebnisse der hier vorgestellten Modelle zur Grundtonermittlung wurden nicht deswegen einer Kritik unterzogen, weil sie einander widersprächen oder dem Autor ein besserer Algorithmus zur Verfügung stünde, sondern weil sie seiner Erfahrung von Tonalität als eben jenem umfassenden Kontext entgegenstehen, der die Bedeutung von Akkorden und Grundtönen überhaupt erst verbürgt. (In welches Dilemma ein Vorgehen gerät, das von dieser Erkenntnis abzusehen wünscht, weil es glaubt sich im Namen der Wissenschaftlichkeit von derartigen ›Voraussetzungen‹ frei machen zu müssen, zeigt sich nirgends besser als bei Parncutt und dessen ›prevailing tonality‹.) Nicht nur, weil die vorgestellten Modelle bereits beim Bestimmen der Grundtöne des konventionellen Akkordrepertoires ›versagen‹, erscheint es zweifelhaft, ob entsprechende Verfahrensweisen in Bezug auf eine Harmonik jenseits der traditionellen Tonalität zu relevanten Ergebnissen gelangen könnten, sondern weil der verlockende Gedanke, in tonal stark erweiterter oder gar ›atonaler‹ (bzw. ›atonikaler‹) Musik auf diesem Wege zugrunde liegende Strukturen freizulegen, letztere bereits als im Prinzip bekannt voraussetzt.[113] Falls der Grundtonbezug das konstitutive Moment der Bildung und des kontextuellen Gebrauchs von Akkorden darstellt (und zwar auch bereits in traditioneller Musik), würde erst die erfolgreiche Integration entsprechender Fragestellungen und Verfahrensweisen in Arbeiten zur Frage der Grundtonbestimmung eine umfassende analytische Perspektive ermöglichen, die ihren Wert für unser Musikverständnis erweisen könnte.[114]
Anmerkungen
Rameau 1722, 4. | |
Ebd., 34ff. | |
Ebd., 49–168; vgl. Christensen 1993, 98–132. | |
Vgl. Schönberg, 1949; insbes. 140–150. | |
Ebd., 417. | |
Ebd., 478–492. | |
Hindemith, 1940, 139. | |
Ebd., 244ff. | |
Ebd., 247–252. | |
Ebd., 254ff. | |
Castel 1722, 1734. | |
Vgl. Rameau 1737, 5–9. | |
Groth 1983, 18. | |
Helmholtz 1913, 386. | |
Helmholtz 1913, 477. Unterstreichungen bedeuten die Erniedrigung der Durterz in der reinen Stimmung gegenüber der gleichschwebenden Temperatur. | |
Ebd., 477f. | |
Ebd., VII. | |
Oettingen 1866, 43, auch Anm. 3; vgl. Helmholtz 1913, 556f. | |
Ebd., 33. | |
Ebd., 32f. | |
Ebd., 31ff. | |
Vgl. Seidel 1966, 45. | |
Vgl. Fricke 2005, 143f. | |
Helmholz 1913, 325–347. | |
Riemann 1875, 205. | |
Ebd., 206. | |
Reinecke 1962; zum ›virtuellen Grundton‹ allgemein vgl. Terhardt 1998, 345–359 und Fricke 2005, 140–149. | |
Smoorenburg 1970. | |
Riemann 1875, 205. | |
Goldbach i.Vorb. | |
de la Motte 1990, 269–274. | |
Billeter 1971, 118f. | |
Thomson 1965, 59f.; später stellte er freilich fest, Hindemiths Theorie sei verdrängt worden, als ab den 1960er Jahren die Schenkeranalyse und der Serialismus die Musiktheorie zu dominieren begannen (ders. 1993, 393f.). | |
Nowka 1999, 651; Holzer 2005, 465. | |
Hindemith, 1940, 90. | |
Ebd., 91. | |
Ebd., 92. | |
Ebd., 102. | |
Ebd., 104. Die Bezeichnung Tritonus kommt nach Hindemith zwar eigentlich nur der übermäßigen Quart zu, »infolge der ständigen Anwendung chromatischer und enharmonischer Bildungen« werde aber nur noch auf dem Notenpapier eine Unterscheidung gemacht, weshalb er auch die verminderte Quinte unter den Begriff Tritonus fasst. | |
Ebd., 92f. und 103. Billeters Forderung daher »nur die Quinte und Quarte und, in Ermangelung dieser, die große Terz und kleine Sexte« zur Grundtonbestimmung heranzuziehen (Billeter 1971, 133) mag auf den ersten Blick methodisch sauberer wirken, verstärkt jedoch die schon bei Hindemith vorhandene Fixierung auf Quinte und Quarte zur Grundtonbestimmung, die – wie im Folgenden gezeigt – zu falschen Ergebnissen führen kann. | |
Ebd., 119f. | |
Ebd., 121. | |
Ebd. | |
Nowka 1999, 651. | |
Z.B. in Will You Love me Tomorrow, auf: Carole King, Tapestry, Ode Records 1971 (CD Sony 1999), Track 9, die genannte Harmonieverbindung erstmals 0:10–0:14. | |
Spinning Wheel, auf: Blood, Sweat and Tears, Definitive Collection, Sony 1995, Track 1. Die Verbindung ist eine Reduktion der Stimmen von Bläsern und Bass in 1:30–1:46 und 2:38–2:53, wobei die Bläser statt des vierten Akkords eine Unisono-Verbindung spielen. In 2:57–3:30 erklingt dieser vierte Akkord, dafür sparen die Bläser den dritten Akkord aus. | |
Holzer 2005, 465. | |
Terhardt 1982. | |
Ebd., 25. | |
Ebd., 24. | |
Ebd., 23. | |
Ebd., 26f. Aus den weiteren Ausführungen Terhardts wird deutlich, dass die Tonhöhenwahrnehmung des Schlagtons vermutlich von den drei höchsten im Beispiel notierten Teiltöne abhängig ist. | |
Ebd., 27–36. Die Experimente messen nur das Grundtonempfinden in zwei- bis dreistimmigen Terzenklängen. Sie beweisen bestenfalls, dass überhaupt Grundtöne gehört werden, ohne dies auch für komplexere Klänge zu belegen. Außerdem setzen die Experimente voraus, der Grundton eines d-Moll-Akkords sei d (Terhardt 1977, 387). Wie noch gezeigt wird, widerspricht Terhardts Theorie der Grundtonbestimmung aber dieser Ansicht. | |
Terhardt 1982, 39. | |
Ebd. | |
Ebd., 41. | |
Parncutt 1989, 8. | |
Terhardt 1982, 44. | |
Parncutt 1989, 8. | |
Terhardt 1982, 42. | |
Ebd. | |
Ebd. | |
Ebd. | |
Leman 1999, 187. | |
Ders. 1995, 44–52, 89–97, 107–113. | |
Toiviainen 2001, 146. | |
Cufaro Petroni und Tricarico 1997, 172. | |
Rowe 2000, 513–517. | |
Parncutt 1988, 66f. | |
Ebd., 73; vgl. Terhardt, Stoll und Seewann 1982b, 684f. | |
Parncutt 1988, 74. Diese Werte zur Gewichtung der potentiellen Akkordgrundtöne scheinen ein wenig zu willkürlich, zumal die von Parncutt gerundeten Werte 1,00, 0,5, 0,33, 0,25 und 0,2 bei Addition eine Genauigkeit von zwei Nachkommastellen suggerieren. | |
Ebd., 74f. | |
Ebd., 77. | |
Ebd., 76. | |
Ebd. | |
Die kleine Terz fehlt hier bei Parncutt. | |
Parncutt 1988, 87f. | |
Ebd., 89f. | |
Ebd., 88. | |
»For example in romantic and jazz harmony […] M3s are usually voiced below m3s (m10s or A9s)« (ebd., 87). | |
In der für diesen Zusammenhang aufgeführten Untersuchung nimmt er die Korrektur der Werte noch nicht vor. In einem der drei im Artikel geschilderten Experimente präsentierte Parncutt in insgesamt 60 Durchgängen jeweils erst einen Akkord und darauf einen der zwölf chromatischen Töne. Die Probanden sollten nun die Zugehörigkeit des Ton zum Akkord auf einer Skala von 0 (Ton und Akkord haben keine Beziehung zueinander) und 3 (Ton ist Akkordton) bewerten. Aus dem Ergebnis, dass er für die Akkordtöne und hier vor allem für den Grundton die höchsten Werte erhielt, folgerte er eine weitgehende Bestätigung seines Modells. Da er aber die fünf präsentierten Akkordtypen (Dur-Dreiklang, Moll-Dreiklang, Dur-Akkord mit kleiner Septime, halbverminderter Septakkord, verminderter Septakkord) anscheinend nur in Grundstellung anbot, belegt der Versuch m.E. zunächst nur, dass der tiefste Ton eines Akkordes am besten wahrgenommen wird (vgl. Parncutt 1993, 38–41 und 46f.). | |
Parncutt 1997, 185 und 187. | |
Ebd., 185 und 188. | |
Ebd., 185f. und 189. | |
Ebd., 186 und 189. | |
Ebd., 190. | |
Ebd., 196f. | |
Balsach 1994. | |
Ders. 1997. | |
Hofmann-Engl 2004. | |
Carreras u.a. 1999, 312ff. | |
Balsach 1994, 14; ders. 1997, 250. | |
Ders. 1997, 251. Die Berechnung dieses Werts bleibt Balsach schuldig. Zwar verweist er auf die Erstfassung der Theorie, doch dort erklärt er lediglich, dass nur eine Minderheit von Akkorden (6%) nicht auf diese Weise zu analysieren sei (ders. 1994, 14). | |
Ders. 1997, 254; vgl. ders. 1994, 15. | |
Ders. 1997, 247. In der Erstfassung diskutiert Balsach dieses Problem noch nicht; vermutlich stammen diese Gedanken aus seiner Auseinandersetzung mit den Modellen von Terhardt und Parncutt. Aus Balsachs Argument, a-Moll könne nicht die Dominante zu D-Dur sein, folgt jedoch, dass a-Moll wegen seines Grundtons c eine Dominante zu F-Dur wäre. | |
Vgl. die Akkordtabelle in Balsach 1994, 57, hier Akkorde mit 5 Tönen, Nr. 11 (II), 60 (V) und 47 (I). | |
Ebd., 56, hier Akkorde mit 4 Tönen, Nr. 13 (II), 32 (V) und 18 (I). | |
Hofmann-Engl 2004, Kap. 1. | |
Ebd., Kap. 2. | |
Rameau 1722, 4; Oettingen 1905, 130; Hindemith 1940, 55ff. | |
Auch Martin Vogel, ein nachdrücklicher Verfechter der ›Naturseptime‹, erklärt, dass sich »das Ohr jedoch nur schwer« auf das Intervall 8:11 einstellt (1962, 45). | |
Eberlein 1993, 483. | |
Ebd. | |
Vgl. Ruschkowski 1998, 238. | |
Terhardt 1979, 178f. | |
Ders., Stoll und Sewann 1982a, 277. | |
Die wohl fälschliche doppelte Angabe »D3« schon ebd. | |
Hier ist nicht der Raum, diesen Algorithmus Terhardts zu untersuchen, die Anwendung ist aber durch ein frei verfügbares Programm, das diesen Algorithmus implementiert hat, unproblematisch (vgl. Jensen 2005). Die Eingabe der bei Terhardt (1979, 178f.) gegebenen Werte führt zu den dort mitgeteilten Ergebnissen. | |
Aus dieser Grenze folgt, das Männergesangvereine offensichtlich grundtonlos singen. | |
Der entgegengesetzte Fall wäre Riemanns Untertonhypothese, in der er die akustische Natur so rekonstruierte, wie sie aus musiktheoretischen Erwägungen sein sollte. | |
Hofmann-Engl 2004, Kap. 2. | |
Oettingen 1866, 75. In einer späteren Fassung seines Harmoniesystems gibt er ein Beispiel für eine eigene Komposition, die mit einer echten ›phonischen Kadenz‹ schließt (ders. 1913, 137ff.). Freilich verweist von Oettingens Argumentation gerade in dieser Frage darauf, dass er sich durch häufiges Hören seiner ›phonischen Kadenz‹ so an den Klang gewöhnte, bis ihm diese Akkordfolge zur Norm wurde: »Ob nun die Forderung, die [Tonica] a im Baß zu hören, für den Schlußaccord wirklich physikalisch und physiologisch begründbar, oder ob es nur Folge einer Verwöhnung unseres Ohres ist, scheint sehr schwer zu entscheiden.« (Ders. 1866, 76; eckige Klammern bei von Oettingen) | |
William Thomson beispielsweise hält denn auch einen solchen Versuch für sinnlos (2004, 440f.). | |
Ich danke Torsten Anders für zahlreiche Anregungen und Korrekturen sowie Johannes Riemenschneider für seine Hilfestellung bei der Rezeption von Terhardts frühen Arbeiten. |
Literatur
Balsach i Peig, Llorenç (1994), La Convergència Harmònica. Morfogènesi dels Acords i de les Escales Musicals, Barcelona: Clivis Publications.
––– (1997), »Application of Virtual Pitch Theory in Music Analysis«, Journal of New Music Research 26, 244–265.
Billeter, Bernhard (1971), »Ist Hindemiths ›Unterweisung im Tonsatz‹ für die harmonische Analyse geeignet?«, Hindemith-Jahrbuch 2, 114–136.
Carreras, Francesco / Marc Leman / Micheline Lesaffre (1999), »Automatic Harmonic Description of Musical Signals Using Schema-Based Chord Decomposition«, Journal of New Music Research 28, 310–333.
Castel, Louis Bertrand (1722), »Traité de l’harmonie reduite à ses principes naturels«, Journal de Trévoux Oktober/November 1722, 1713–1743, 1876–1910, Reprint in: The Complete Theoretical Writings of Jean-Philippe Rameau, hg. von Erwin R. Jacobi, Bd. 1, Dallas/Texas: American Institute of Musicology 1967, XVII–LIII.
Christensen, Thomas (1993), Rameau and Musical Thought in the Enlightenment, Cambridge: Cambridge University Press.
Cufaro Petroni, Nicola / Matteo Tricarico (1997), »Self-Organizing Neural Nets and the Perceptual Origin of the Circle of the Fifths«, in: Music, Gestalt and Computing. Studies in Cognitive and Systematic Musicology (= Lecture Notes in Artificial Intelligence 1317), hg. von Marc Leman, Berlin u.a.: Springer, 169–180.
Eberlein, Roland (1993), »Konsonanz«, in: Musikpsychologie. Ein Handbuch, hg. von Herbert Bruhn, Rolf Oerter und Helmut Rösing, Reinbek: Rowohlt, 478–486.
Fricke, Jobst P. (2005), »Psychoakustik des Musikhörens. Was man von der Musik hört und wie man sie hört«, in: Musikpsychologie (= Handbuch der Systematischen Musikwissenschaft 3), hg. von Helga de la Motte-Haber u. Günther Rötter, Laaber: Laaber, 101–154.
Goldbach, Karl Traugott (i.Vorb.), »Mythos Untertonreihe«, in: Mythos – Helden – Symbole. Legitimation, Selbst- und Fremdwahrnehmung in der Geschichte der Naturwissenschaften, der Medizin und der Technik, hg. von Siegfried Bodenmann und Susan Splinter, München: Meidbauer.
Groth, Renate (1983), Die Französische Kompositionslehre des 19. Jahrhunderts (= Beihefte zum Archiv für Musikwissenschaft 22), Wiesbaden: Steiner.
Helmholtz, Hermann von (1913), Die Lehre von den Tonempfindungen als Grundlage für die Theorie der Musik, 6. Aufl., Braunschweig: Vieweg.
Hindemith, Paul (1940), Unterweisung im Tonsatz. Theoretischer Teil, 2. Aufl., Mainz: Schott.
Hofmann-Engl, Ludger (2004), »Virtual Pitch and its Application to Contemporary Harmonic Analysis«. http://www.chameleongroup.org.uk/research/link_virtual_analysis.html
Holzer, Andreas (2005), »Eigensysteme von Komponisten«, in: Musiktheorie (= Handbuch der Systematischen Musikwissenschaft 2), hg. von Helga de la Motte-Haber und Oliver Schwab-Felisch, Laaber: Laaber, 461–474.
Jensen, Jeff (2005), A Java Applet to Calculate Virtual Pitch. http://jjensen.org/VirtualPitch.html
La Motte, Diether de (1990), Harmonielehre, 7. Aufl., München: dtv.
Leman, Marc (1995), Music and Schema Theory. Cognitive Foundations of Systematic Musciology (= Springer Series in Information Sciences 31), Berlin u.a.: Springer.
––– (1999), »Relevance of Neuromusicology for Music Research«, in: Journal of New Music Research 28, 186–199.
Nowka, Dieter (1999), Europäische Kompositionsgeschichte. Material. Verfahren. Komposition, Landsberg/Lech: Ecomed.
Oettingen, Arthur von (1866), Harmoniesystem in dualer Entwickelung. Studien zur Theorie der Musik, Dorpat und Leipzig: Gläser.
––– (1904), »Das duale System der Harmonie: III. Akustische und musikalische Konsonanz«, Annalen der Naturphilosophie 4, 116–136.
––– (1913), Das duale Harmoniesystem, Leipzig: Siegel.
Parncutt, Richard (1988), »Revision of Terhardt’s Psychoacoustical Model of the Root(s) of a Musical Chord«, Music Perception 6, 65–94.
––– (1989), Harmony: A Psychoacoustical Approach (= Springer Series in Informations Sciences 19), Berlin u.a: Springer.
––– (1993), »Pitch Properties of Chords of Octave-Spaced Tones«, Contemporary Music Review 9, 35–50.
––– (1997), »A Model of the Perceptual Root(s) of a Chord Accounting for Voicing and Prevailing Tonality«, in: Music, Gestalt and Computing. Studies in Cognitive and Systematic Musicology (= Lecture Notes in Artificial Intelligence 1317), hg. von Marc Leman, Berlin u.a.: Springer, 181–199.
Rameau, Jean Philippe (1722), Traité de l’harmonie reduite à ses principes naturels, Paris: Ballard, Reprint hg. von Erwin R. Jacobi, Dallas, TX: American Institute of Musicology 1967 (= The Complete Theoretical Writings of Jean-Philippe Rameau 1).
––– (1737), Génération harmonique ou traité de musique théorique et pratique, Paris: Ballard, Reprint Dallas, TX: American Institute of Musicology, 1968 (= The Complete Theoretical Writings of Jean-Philippe Rameau 3).
Reinecke, Hans Peter (1962), »Hugo Riemanns Beobachtung von ›Divisionstönen‹ und die neueren Anschauungen zur Tonhöhenwahrnehmung«, in: Hans Albrecht in Memoriam. Gedenkschrift mit Beiträgen von Schülern und Freunden, hg. von Wilfried Brenecke und Hans Haase, Kassel: Bärenreiter, 232–241.
Riemann, Hugo (1875), »Die objektive Existenz der Untertöne in der Schallwelle«, Allgemeine deutsche Musikzeitung 2, 205f. und 213ff.
Rowe, Robert (2000), »Key Induction in the Context of Interactive Performance«, Music Perception 17, 511–530.
Ruschkowski, André (1998), Elektronische Klänge und musikalische Entdeckungen, Stuttgart: Reclam.
Schönberg, Arnold (1949), Harmonielehre, 4. Aufl., Wien u.a.: Universal Edition.
Seidel, Elmar (1966), »Die Harmonielehre Hugo Riemanns«, in: Beiträge zur Musiktheorie des 19. Jahrhunderts, hg. von Martin Vogel (= Studien zur Musikgeschichte des 19. Jahrhunderts 4), Regensburg: Bosse, 39–92.
Smoorenburg, Guido F. (1970), »Pitch Perception of Two-Frequency Stimuli«, Journal of the Acoustical Society of America 48, S. 924–942.
Terhardt, Ernst (1974), »Pitch, Consonance, and Harmony«, Journal of the Acoustical Society of America 55, 1061–1069.
––– (1977), »The Two-Component Theory of Musical Consonance«, in: Psychophysics and Physiology of Hearing, hg. von Edward Frank Evans und John Patrick Wilson, London u.a.: Academic Press, 381–390.
––– (1979), »Calculating Virtual Pitch«, Hearing Research 1, 155–182.
––– (1982), »Die psychoakustischen Grundlagen der musikalischen Akkordgrundtöne und deren algorithmische Bestimmung«, in: Tiefenstruktur der Musik. Festschrift Fritz Winckel zum 75. Geburtstag, hg. von Carl Dahlhaus, Manfred Krause u. Peter Frenzel, Berlin: TU Berlin, 23–50.
––– (1998), Akustische Kommunikation, Berlin: Springer.
–––– (1982a) / Gerhard Stoll / Manfred Seewann, »Pitch of Complex Signals According to Virtual-Pitch Theory: Tests, Examples, and Predictions«, Journal of the Acoustical Society of America 71, 671–678.
––– (1982b), »Algorithm for Extraction of Pitch and Pitch Salience from Complex Tonal Signals«, Journal of the Acoustical Society of America 71, 679–688.
Thomson, William (1965), »Hindemith’s Contribution to Music Theory«, Journal of Music Theory 9, 52–71.
––– (1993), »The Harmonic Root: A Fragile Marriage of Concept and Percept«, Music Perception 10, 385–416.
––– (2004), »From Sounds To Music: The Contextualizations of Pitch«, Music Perception 21, 431–456.
Toiviainen, Petri (2001), »Real-Time Recognition of Improvisations with Adaptive Oscillators and a Recursive Bayesian Classifier«, Journal of New Music Research 30, 137–147.
Vogel, Martin (1962), Der Tristan-Akkord und die Krise der modernen Harmonielehre (= Orpheus Schriftenreihe zu Grundfragen der Musik 2), Düsseldorf: Verlag der Gesellschaft zur Förderung der systematischen Musikwissenschaft e.V.
Dieser Text erscheint im Open Access und ist lizenziert unter einer Creative Commons Namensnennung 4.0 International Lizenz.
This is an open access article licensed under a Creative Commons Attribution 4.0 International License.