Music Theory: Speculation, Reasoning, Experience

1. Introduction

The term ‘music theory’ carries more than one meaning. It may denote, on the one hand, an approach in which theory concerning music in some sense is fundamental, as in works devoted to the very ‘logic’ of music or to its equivalent, a thorough mathematical treatment of musical elements and structures.[1] Also, one may think of a philosophical or anthropological theory of music that would qualify as ‘music theory.’[2] On the other hand, many works usually reckoned among ‘music theory’ serve a practical purpose, in the first place. In this respect, one may point to the multitude of textbooks on harmony, many of which were written by composers like Nikolai Rimsky-Korsakov, Arnold Schoenberg, or Walter Piston. Of course, such works may contain some genuine ‘theory’ (meaning rational constructs based on certain axioms or similar fundamental assumptions as well as including hypotheses, models and a coherent treatment of certain problems) besides a more practical orientation. For example, Paul Hindemith’s Unterweisung im Tonsatz contains a proposal of how to calculate a musical scale from harmonic partials,[3] and draws substantially on the psychoacoustic phenomenon of combination tones. Schoenberg’s Harmonielehre (1911), on the other hand, in its final chapter offers some ideas concerning the possibility to create a ‘Klangfarbenmelodik.’ The remarks he gives are not quite clear, and hypothetical at best; one must, therefore, try to ‘translate’ his ideas into an empirically meaningful description suited to allow experimental investigation.[4]

Currently, music theory may include subjects ranging from elementary harmony and counterpoint to advanced models of musical grammar and syntax, and may be based on various methods ranging from solfège and demonstrations at the piano to computer simulation of generative processes (e.g., improvisation). There are some comprehensive historic surveys of approaches to ‘western’ music theory (from antiquity to the first half of the 20^th century[5]); also, some major publications focus on more recent research trends, many of which have been heavily influenced by the cognitive sciences.[6]

The complexity of matters of course increases if one attempts to cover music theoretical systems of areas such as Northern and Southern India, Persia, the Arab cultures or major parts of China. One simply has to notice that research on non-western music cultures and their theoretical systems including conceptualizations (either accessible from written sources or, if transmitted only in an oral format, by fieldwork) has been intensified over the past decades.[7] Of course, there are concepts of ‘music theory’ found in particular in Near and Middle Eastern cultures (as well as in parts of Northern India) that not only converge to some extent among each other but which are historically related also to ‘classical’ Greek music theory.[8]

Though music theory is by no means restricted to ‘western’ culture, it gained a special status first in Greek antiquity,[9] and later in European as well as in Asian countries that participated in the lore that had been established in Greece and in Greek colonies in the south of the Italian peninsula.[10] In the section following this introduction, I will briefly relate some aspects of the notion of ‘theory’ as outlined in Greek and medieval sources in order to elucidate the role theory had in regard to fundamental research done in music and mathematics. According to Aristotle,[11] ‘theoria’ means a certain mode of mental activity pursued by subjects who conduct reasoning for its own sake (with little regard to ‘practical applicability’).[12] The term ‘speculatio’ that is found in many Latin sources in certain respects was closely related to the Greek ‘theoria’ (the Greek term ‘theoria’ often was translated into Latin as ‘speculatio’). Terms like ‘speculator,’ meaning ‘scout,’ referred to a certain activity, that of investigation (there was also the term ‘speculator naturae’). It was in the context of Christian theology and philosophy that ‘speculatio’ gained a somewhat different meaning, including aspects of contemplation and meditation. Though ‘theoria’ and ‘speculatio’ allow for contemplation, it does by no means preclude scientific rigor. In a treatise on music-mathematics usually believed to be quite speculative, Kepler’s Harmonice Mundi (1619), there is a thorough mathematical background.[13] Moreover, ‘speculation’ as a means for ‘hypothetical mental construction’ can be regarded as part of scientific heuristics.

As far as Greek music-mathematics and science in general are concerned, there are many indications showing that ‘theoria’ was accompanied by some form of experiment, or that theoretical concepts emerged from insight first gained by experience.[14] The combination of theoretical analysis and empirical research became characteristic for the sciences since the time of Aristotle (and probably even earlier). Systematic musicology that in fact can trace its beginnings to scholars like Archytas, Euclid, and Ptolemy (Klaudios Ptolemaios) pursues such a perspective to the present, though of course with different objectives and methodology.[15] However, the impact Greek music-mathematics and music theory had on research still in the past century is obvious from scholarly studies and monographs such as published by Carl Stumpf (1897, 1898, 1901), Jacques Handschin (1948), and Martin Vogel (1975, 1993).

This fact alone contradicts a claim made by Dahlhaus[16] who held that Greek concepts of music theory, and in particular the Aristotelian notion of ‘theoria’ has been “completely” (restlos) eliminated in modern times in Europe. The new paradigm for music theory, as Dahlhaus[17] saw it, ultimately became (historical) understanding of musical works in regard to their conception and reception. This view of course contains some plain truth: one of the tasks of music theory is to study works of music in regard to structural elements and features, harmonic textures, etc. However, in order to match the notion of ‘theory,’ the study of individual works of music will go beyond technical analysis and description, and may focus on, for example, semiological aspects,[18] or specifics of sound structure as dependent on instrumentation and playing techniques.[19] Also, an analysis (even of single works) not confined to a technical description and hermeneutic interpretation may shed light on more general concepts relevant to sound research, music perception and cognition.[20]

Music theory is by no means restricted to the analysis of single works, or to the description of individual composer’s ‘poetics.’ Such a view would unduly narrow the scope of the discipline. One will notice that Schoenberg, in his Harmonielehre (which in part serves the cause of justifying Schoenberg’s own approach to composition around 1910), maintains a view that is fairly broad in regard to techniques explored in various styles of tonal music.[21] Similarly, Hindemith’s Unterweisung (1940) indeed attempts to present fundamentals of tonal music (with examples spanning various styles and eras) in a textbook format. In addition, there are comprehensive works on tonal music that offer a descriptive and analytic approach including aspects of perception and apprehension.[22]

Further, music theory has been pursued from a more formal perspective. Thereby, musical elements, structures, and also concepts as such have been subjected to a logical or mathematical treatment.[23] Other approaches are based on concepts derived from structural linguistics (best known perhaps is Lerdahl and Jackendoff 1983). What is common to many contemporary studies in music theory is an orientation towards cognitive aspects, and a methodology that includes algorithmic modelling, signal processing, and/or behavioural experiments.[24] In sum, there is a huge amount of ‘theory’ (conceptualization, system design, etc.), on the one hand, and a tendency to back theoretical reasoning by empiricism, on the other.

2. Theory, Speculation, Empiricism

The beginnings of music theory in Europe, usually attributed to Pythagoras and his school, reveal the importance of numbers, ratios and proportions employed to determine relations of tones and their possible use as intervals. Of course, the ‘logos’ inherent in harmonic relations (‘logos’ meaning relation between two numbers[25]) and their grouping into proportions (representing ratios of ratios, for example 6:9 = 8:12 and 12:9 = 8:6) is of interest as such, on the one hand, and may be applied to fields other than music, on the other. When Aristotle, in his Metaphysics, criticized the “… so-called Pythagoreans …”[26] he did so because they relied, in his view, too much on numbers as well as on relations (as expressed by numbers). Aristotle apparently did object to treating different spheres (e.g., arithmetic, acoustics, music) along the same basic theory. In modern science, mathematical principles and techniques indeed serve as the unifying factor, and mathematics is still most useful for the analysis and description of musical and acoustical phenomena.[27]

Mathematics of the Pythagoreans reconstructed from Greek sources[28] revealed that basic musical intervals (octave 1:2, fifth 2:3, fourth 3:4, major second or ‘tone’ 8:9) could be derived not only by proportions (the Tetraktys 6:8:9:12)[29] built from natural numbers (1, 2, 3, 4) and their multiples but also by geometrical operations. Thereby, one could find additional intervals; for example, the tone 8:9, taken as a segment that is subtracted twice from the section [of a string] representing a fourth 3:4, yields both the ‘Pythagorean’ major third 64:81, and, as a remainder, the ‘leimma’ of 243:256, which is usable as a melodic step. Once it was understood that a line AB of given length can be divided into sections according to certain principles (e.g., the arithmetic, the geometric, and the harmonic mean, respectively[30]), one could apply these principles to a string of a musical instrument or to any other one-dimensional continuum where fixed points constitute intervals among each other. As Ptolemy states, Archytas of Tarent understood how to divide a fourth (4/3) into a Tetrachord whose intervals either conform to the enharmonic, to the chromatic, or to the diatonic genus:[31]

5/4 x 36/35 x 28/27 = 4/3; 32/27 x 243/224 x 28/27 = 4/3; 9/8 x 8/7 x 28/27 = 4/3.

These ratios include the pure major third 5/4, the ‘Pythagorean’ minor third 32/27, the major whole tone 9/8, and a large whole tone 8/7 (≈231 cent). This interval as well as that of 7/6 (≈267 cent) is found in descriptions of Tetrachords, of which Ptolemy says they were in use among the players of the kithara.[32] Given the scheme of constructing intervals by sequences of pure fifths,[33] one would expect a major third defined as a Ditonos (81/64) instead of the pure major third 5/4. However, it takes but little effort to change the procedure so that ratios of 5/4 and 6/5, or, alternatively 7/6 and 8/7 will be obtained.[34] The Sectio canonis attributed to Euclid demonstrates how divisions and multiples of sections (of a single string) can be used to establish the fundamental structure of the Greek tone system.[35]

It is quite likely that calculations accompanied experimental work. As Arpád Szabó states, basic concepts such as ‘diastema’ (= interval) “… could never have been originated without musical experiments using the canon.”[36] It is likely that Archytas “… attempted both to analyse the attunements underlying contemporary musical practice, and to reveal the principles of mathematical order on which they were based.”[37] Even seemingly abstract constructs concerning numbers and magnitudes, which Aristotle[38] attributes to Plato and (before him) the Pythagoreans, and finds cumbersome to explain, can be translated into a scheme that includes all basic music intervals.[39] Further, one will note that the two series disclosed in Plato’s Timaios (35b), which can be written as 1 : 2 : 4 : 8 (=1 : 2¹ : 2² : 2³) and 1 : 3 : 9 : 27 (=1 : 3¹ : 3² : 3³), were discussed also in much later writings on music theory (with more ‘practical’ objectives, as in Rameau 1750; see below). In general, Greek mathematics can be translated into modern formulations. One may point to the so-called Aristoxenus/Euclid-controversy concerning the division of the whole tone 8/9 into two or more (equal) parts. The proof Euclid laid down to show that it is not possible (with respect to a geometric series) to insert a natural number between two natural numbers whose relation is (n+1):n can be stated in terms of modern arithmetic.[40] Similarly, the problem Ptolemy raises[41] whether the Aristoxenians were correct saying that the octave comprises six whole tones (9/8) can be easily subjected to algorithmic probing. Whereas Ptolemy had to rely on fractions to find the difference between (9/8)^6 = 531441/262144 and the octave (2/1), which is 7153/262144, one can now proceed by finding a set of solutions which must satisfy the equation[42]

Solve[(x^6) / (8^6) = 2, x]//N and, alternatively

Solve[(9^6) / (x^6) = 2, x]//N

The set of solutions includes x = 8.9797 for the numerator, and x = 8.01809 for the denominator. Hence, the problem of giving six whole tones such a size as to make up exactly one octave, would be solved if the ratio of fundamental frequencies between each two tones would equal a real number k = 1.12246, which in turn corresponds to 200 cents (the interval of the whole tone in 12-tone equal temperament). Such a calculation (which involves logarithms) was neither available to Aristoxenus nor to Ptolemy. The ‘overshoot’ of the six whole tones (9/8^6) over the octave (2/1) of course sums up to 24 cent (a ‘Pythagorean’ comma). Ptolemy objected that neither calculation (based on fractions) nor tuning an eight-string ‘Kanon’ and listening to the resulting pitches would confirm Aristoxenian opinions. His own estimate of the difference between six tones (9/8^6) and the octave is about 65/64 (≈27 cent), which is close to the exact numerical solution, and within the limits of auditory discrimination.

Notwithstanding possible ‘practical’ applications,[43] Pythagorean music-mathematics was a field of ‘theoria’ in the sense that the logical coherence of arguments and explanations is the decisive criterion which philosophical, mathematical or any other scientific investigations must fulfil. According to Aristotle,[44] in particular sciences dealing with causes and principles (e.g., physics, philosophy) are ‘theoretical’ in that their approach is analytic and reflective rather than suited to guide human behaviour or (artistic or other) production. When it comes to scientific reasoning, there is a clear hierarchy for Aristotle leading from perception to experience and then further on to true knowledge.[45] The analytic (and in part contemplative) nature of ‘theoria’ as pronounced by Aristotle as well as Platonic ‘ideas’ were well preserved in the long tradition that can be traced from Greek and Hellenic sources to Boethius and the Middle Ages. It included basic essentials of Pythagorean lore,[46] which was still of influence in the 16^th and 17^th centuries, respectively. However, by that time a basically ‘Pythagorean’ way of thinking had been complemented more and more by empirical observation (as is obvious in writings of, for example, Zarlino and Kepler, respectively; see below).

As to science in regard to nature, Aristotle combines analytic inquiry with consideration of factual evidence.[47] One would not call him, though, an ‘empiricist’ (which has modern connotations). His one-time student, Aristoxenus of Tarent, has been lauded for having introduced ‘strict empiricism’ into the study of music. No doubt there are significant differences between scholars like Archytas and Euclid (who proceed from a mathematical background to the study of empirical phenomena), on the one hand, and Aristoxenus (who had a thorough musical understanding and first-hand experience of musical practice), on the other. Of course, there were controversial arguments concerning, for example, the nature and size of intervals (viewed either as a mere ‘distance’ between two points, or as a relation of two tones resulting in a certain musical and perceptual quality) as well as other issues.[48] However, there is some common ground shared by ‘Pythagoreans’ and ‘Aristoxenians,’ and there have been attempts to present a more integrative approach, in which mathematics, acoustics, and perception are taken into account as is the case in the Harmonics of Ptolemy. He clearly saw the bias in the work of some of his predecessors, on the one hand, but could make use of all the previous findings, on the other.

There is no need to emphasize that a science of music (musica scientia) needs both orientations, analytic ‘theoria’ as well as experimental work. The Greek ‘Kanon’ was in fact a device to carry out measurements, and the monochord in medieval times was reckoned as an instrument that could and should be used for measurement and ‘probing.’[49] At the same time, it was regarded fundamental to demonstrate the correctness of calculations. The monochord, in this respect, is a geometrical tool as well as a ‘principle.’ The multitude of proportions (many of them representing Greek tone systems and music theory) found in sources like the Speculum musicae (ca. 1330) of Jacobus of Liège reflects the erudition of the time.[50] However, there were factors that brought about change in regard to music theory as well as to science in general. Scholars certainly were taking up and expanding Aristotelian ‘empeiria’ (as was advocated by Roger Bacon[51]). There are indications that, probably beginning around 1300, empirical investigations gained more of an interest. One may point to early contributions to the theory of vibration (including elements of pitch perception) made by Pietro d’Abano of Padua around 1310,[52] and to Nicole Oresme (1320–1382) who it seems was discovering harmonic partials.[53] Also, one has to remember that building musical instruments such as organs required both calculations and some experience with respect to the mensuration of pipes. Apparently during the 14^th century, a strictly Pythagorean approach to mensuration based on simple integer proportions (that seems to have governed the type of medieval organ known as ‘Blockwerk’[54]) was followed by variable mensuration that lend itself to experimentation. Constructing organs with several ranks of pipes that had different length (usually expressed in foot, e.g. 8’, 4’, 2 2/3’, etc.) meant that pipes were sounding harmonic intervals simultaneously even if one would have played a single melodic line.

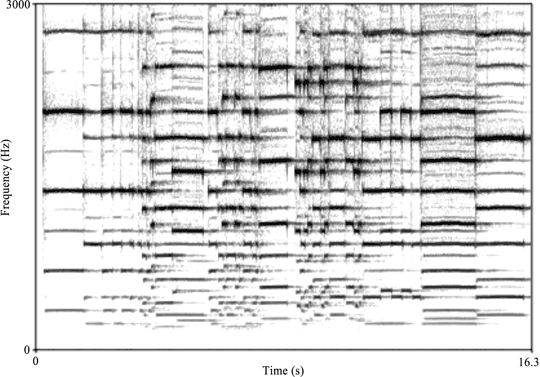
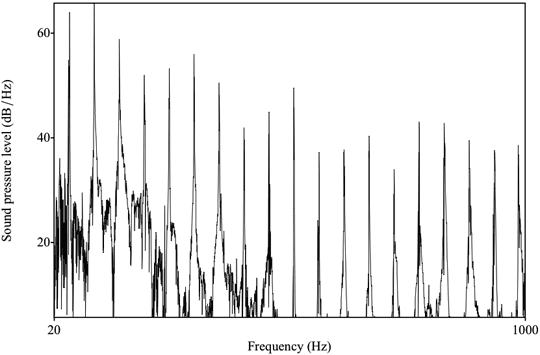
Probably the oldest preserved organ in Europe still playable is that of Sion (Valais; Sitten, Wallis). Three stops in 4’, 2’ and 1 1/3’ foot that can be dated to ca. 1400 are extant.[55] As regards the music that might have been played on an organ corresponding to the Sion instrument in the 2^nd half of the 14^th century, the repertoire would have included instrumental adaptations of various vocal forms as well as maybe some original pieces conceived for execution on the organ.[56] Most of the musical settings show parallel intervals (with a predominance of the perfect fifth, and a rare major third occurring here and there) so that listeners were exposed to consonant intervals enriched by the harmonics of the pipes used for the respective piece. The beginning of the Estampie Retrove from the Robertsbridge codex, when played on the Sion organ, yields a spectral energy distribution as shown (for a frequency range from 0.2 – 3 kHz) in figure 1. It is obvious that the music, if considered in terms of melodic and ‘vertical’ interval proportions actually put into sound, gains a harmonic dimension even when performed on a small ‘Gothic’ organ. Though the interval proportions were regarded as constitutive elements of the syntactic structure, and may be understood as such by appreciative listeners, the experience of music as performed must have added to the insight that the concept of ‘consonance’ in fact relates to sounds that ‘fit’ together.

Figure 1. Spectrogram (0.2 – 3 kHz) of the first phrases of the Estampie Retrove, played on the organ of Sion (Switzerland)

One can see that evolving musical practice as well as a different evaluation of actual sensation and perception of music were factors that, by about 1400–1500, began to challenge traditional views.[57] Though there was still a fair amount of speculative ‘theoria’ found in treatises on music theory, one has to take into account significant developments in musical acoustics and psychoacoustics that were achieved from the 16th century through the 17th and 18^th centuries, respectively.[58] Areas of research and experimentation that became important included (a) the theory of vibration, the phenomena of resonance and harmonic partials, (b) pitch, pitch perception and pitch relations, (c) tuning and temperament, (d) affective and gestural (rhetorical) quality of music. These fields were part also of music theory, and connected in various ways to musical practice.

For example, Zarlino, who still preferred numbers and proportions as principles for rational deduction of musical scales and intervals, offers a discourse on how notes either high or low in pitch apparently relate to the speed of vibration of a string as well as to its diameter and the tension with which it is stressed.[59] The explanation he offers in part is correct; however, there are some flaws since he seems to believe that the frequency of vibration of a string of given length, tension and diameter would depend, at least to some degree, on the amplitude of vibration.[60] As the amplitude decreases continuously after a string has been plucked, this would result in decreasing frequency of vibration, and hence in a pitch glide downwards. Beeckman, Descartes, Galilei and others noted that this was actually not the case. The correct solution, which needs a theory of isochronous periods of vibration, was found only in the course of the 17^th and 18^th centuries, respectively.[61]

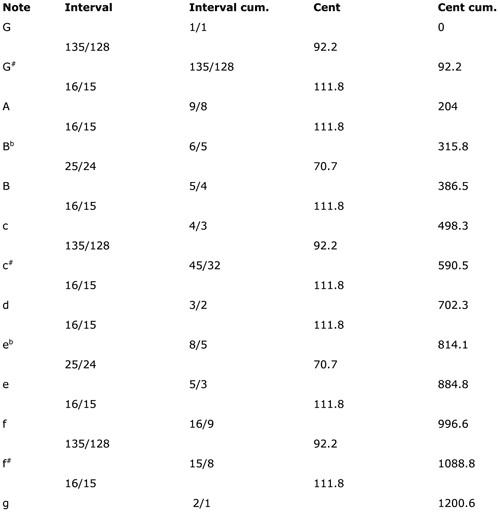
Kepler, after discussing the minor and the major genus and divisions of the octave according to both,[62] finds an optimum solution for a just scale per octave, which, if we transform his list of numbers {2160, 2048, 1920, … , 1080} into common interval ratios plus modern cents,[63] reads as stated in Table 1:

Table 1. Kepler’s calculation of a just scale G-g

Taking this scale resulting from both axiomatic theory and principles of ‘natural’ hearing as a standard, Kepler compares it to another solution that Vincenzo Galilei (1581) had proposed for a scale to be tuned on the lute. Kepler admits that Galilei, by applying ‘mechanical’ principles, namely a sequence of divisions based on the ratio 18/17 (yielding intervals that are nearly 99 cents, and, hence, very close to equal temperament), had found a scale tolerable to the ear (as it would allow certain deviations from just interval proportions) yet not satisfying in the end because the ear, guided by the mind, would not take a ratio of 100.000: 50.363 as representing a perfectly consonant interval. Hence, the ear is viewed as a factor relevant to finding practical solutions that, however, may not be acceptable to the musical mind seeking rational analysis. To Kepler, the ear alone cannot provide the degree of exactitude required for confirming models of musical scales and intervals, which thus is left to mathematical justification.

From what has been outlined so far, it should be clear that music theory was closely related to the Aristotelian notion of ‘theoria,’ and to a general concept of science that combines rational analysis with empirical investigations. Music theory, in this respect, was part of fundamental research (Grundlagenforschung), and also intrinsically tied to philosophy.

The argument that has been put forward repeatedly now is that already the ‘musica poetica’ of the 16^th and 17^th centuries led to a paradigm shift, whereby subjects traditionally covered under the heading of ‘musica theoretica’ are said to have lost as much in interest as subjects bearing on techniques of composing actual music did win. Though one may point to various (if not many) writings treating aspects of musical syntax, musical rhetoric, etc.,[64] one should not forget that, first of all, fundamental research in acoustics, organology, sensation and perception of musical sound developed rapidly during the same era[65] so that ‘musica theoretica’ flourished again (though taking some new directions close to mathematics, physics, medicine, etc.). Given the factual evidence, it would be inappropriate to say that ‘musica poetica’ (a movement that rose to prominence especially in parts of Germany) did supersede ‘musica theoretica’ (as continued and developed by Zarlino, Vicentino, Galilei, Descartes, Mersenne, Doni, Kepler, Sauveur, Huygens, Euler, Tartini, etc.). Moreover, a significant portion of ‘New Music’ composed around 1600 did profit not only from antique music theory (even if misinterpreted in certain ways), but also from the experimentalism that had become a true paradigm.[66]

In the following sections, I will further explore relations between theoretical reasoning, speculation (touching on both heuristics and imagination), and empiricism in regard to music theory. Accepting the limitations of an article, a selection of case studies will be presented, each of which seems suited to discuss issues that have been of relevance to music theory. The first case study considers relations between harmonically differentiated compositional structure (as found in chromatic and enharmonic settings from the 16^th century onwards), tunings, and intonation. Next, Rameau’s interest in acoustical phenomena (often disapproved of as a shift towards ‘physicalism’ in music theory) is given a brief assessment; there are some recent attempts at giving harmony (psycho)acoustical foundations, which relate to Rameaus’s ideas one way or another. Since Rameau (and almost all theorists that have followed him since) faced severe problems when dealing with the minor tonality, he devised a basically ‘dualistic’ model to account for both harmonic major and harmonic minor. While some believe ‘harmonic dualism’ is obsolete and dead, the problems it was devised to solve unfortunately are not. In the third of the case studies, some steps in the development of harmonic dualism are retraced in brief, in order to illustrate certain problems. In each of the three case studies, I have added a few measurements and data to my arguments where appropriate to underpin the idea that empiricism might go well along with ‘theory,’ and that some of the pertinent problems should be restudied including experimental methodology.

3. Case Studies: from Vicentino to Riemann

3.1 Chromaticism, tunings, intonation

One can study the relation of theory to practice, for example, in the area of chromatic and enharmonic tone systems, scales, and intonation. It has been asserted more than once that much of the chromaticism found in works of the 16^th and 17^th century was a regionally rather limited and historically short-lived stylistic trend, and that the usage of enharmonic features was even more restricted because, on the one hand, instruments suited to perform such music would have been extremely rare, and, on the other, vocalists would hardly be capable to master the subtle intonation differences implied by tonal structures found in, for example, Gesualdo’s later madrigals (of his 5^th and 6^th books of madrigals). In short, it was held that such music was a matter of ‘speculative theory’ rather than relevant to practice.

Meanwhile, the whole issue of chromaticism and ultra-chromaticism as well as enharmonic experimentation has been subjected to scrutiny including reconstruction of instruments, performance practice, and empirical investigation.[67] As to chromaticism, sources from the Faenza codex onward allow one to reveal tonal structures that can be systematized in a rational way.[68] Systems of tuning and temperament from the Middle Ages well into ‘modern’ times have been carefully investigated, and have been given precise mathematical description.[69] Also, it has been shown that the occurrence of consonances and dissonances in musical compositions of the 16^th–18^th centuries is not independent of the tuning systems in use at the time (Pythagorean, Just, Meantone[70]). For example, keyboard adaptations of Dowland’s Lachrimae Pavan (1604 or earlier) as elaborated by J. P. Sweelinck and M. Schildt, respectively, as well as many works of the time (like the Galiarda Dolorosa of Peter Phillips) require a meantone tuning, which offers as much as eight pure major thirds 5/4. The harmonic structure of those works can only be realized with a tuning that allows to preserve the ‘sweetness’ of simultaneous thirds and sixths. In this respect, the correct tuning certainly is an intrinsic part of the work in question, and not just an attribute from the exterior. Listening to the Paduana Lachrymae or to other works evidently written to be performed in specific tunings and temperaments probably is enough to understand how problematic is the view (motivated by aesthetics), according to which the ‘intentional’ (compositional structure represented as a score based on symbolic notation) is the ‘interior’ of music that is of relevance to music theory, whereas the ‘acoustical exterior’ (actual realization by means of sounds organized according to tone systems and tunings) is of but marginal interest.[71] One can of course distinguish syntactic structure as put to paper and musical execution of a given work resulting in sound; however, the juxtaposition of ‘interior’ and ‘exterior’ (or, likewise, ‘intentional’ versus ‘accidental,’ ‘compositional’ versus ‘acoustical,’ ‘historical’ versus ‘natural,’ etc.) is not quite plausible when viewed from a musical perspective. Still far in the 19^th century, Anton Bruckner, famous as a composer, recognized that compositional structures (such as modulations between distant keys) should be executed in a musically differentiated way (namely, in just intonation[72]).

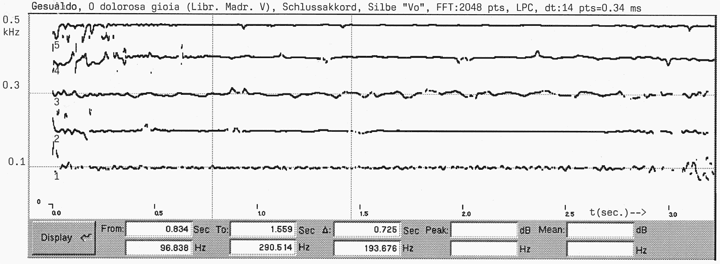
Microtonal systems, as they emerged in the course of the 16^th century, became executable both on a variety of instruments as well as for vocalists. Music written by Nicola Vicentino (1555) that comprises enharmonic tone steps in melody and some uncommon simultaneous intervals can be alternatively performed in the diatonic, in the chromatic, or in the enharmonic genus.[73] The latter two of course require professional singers (unspoiled by vibrato techniques that are common use among bel canto singers) and constant training. One can check the quality of intonation either by ear or by empirical measurement based on digital signal processing.[74] To demonstrate how subtle intonation in fact can be, an analysis of the final chord of the madrigal O dolorosa gioia (from Gesualdo’s Libro V°) as performed by The Consort of Musicke (London) is given.[75] The final G-major chord, sung on the syllable vo (… e vi – vo), consists of the notes G-g-d¹-g¹-b¹. The overall pitch pattern realized by the five voices can be seen when tracking their fundamental frequencies, which was done by a LPC algorithm.[76]

Figure 2. LPC analysis of final chord, O dolorosa gioia, The Consort of Musicke

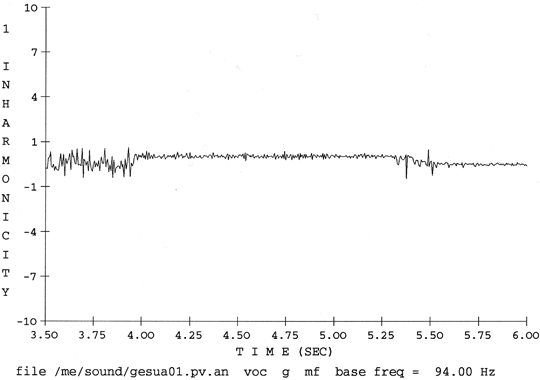
According to the sound analysis, the soprano, the tenor and also the bass are exceptionally stable in their intonation once they have matched their voices to the fundamental frequencies required for the G-major chord. Looking into details of pitch adjustments one finds, for example, the bass succeeds in producing a stable fundamental frequency (of the note G) for ca. 1.5 seconds after some initial fluctuation. Bass, tenor and soprano in this chord realize fundamental frequencies representing just intonation pitches in a perfect manner (the other two voices being a few cents sharp).

Figure 3. Tracking of the bass voice in the final chord of O dolorosa gioia

Recordings by singers and ensembles trained to perform in highly chromatic or even enharmonic genres[77] demonstrate that intonation according to an elaborate scale and chord structure is possible. However, the singer must know which pitch representing a certain note she or he is expected to realize is the correct one in a given structure of intervals, chords and sonorities.[78] Whereas the intonation of the final chord in O dolorosa gioia, or in almost any other work, will hardly pose a problem as to the required pitches and respective fundamental frequencies, intonation patterns for chords and other sonorities found in works of music must be determined by analysis that, as a matter of fact, has to precede performance. In this respect, one needs to study, depending on the genre and style of the music in question, both the single voices and the relations they form in regard to ‘concordant’ and ‘discordant’ intervals[79] and the ‘vertical’ chord structure that emanates from (in particular, rhythmically conjoint) voices sounding simultaneously. Depending on a weighting of the two factors (counterpoint and harmony), different solutions in regard to intonation for a certain piece (or of some part of a piece) are feasible. One has to compare different solutions by checking their musical ‘plausibility’ as well as their sonorous coherence; this of course requires that different solutions must be realized in sound either on conventional musical instruments (including the singing voice), or with the aid of computers and synthesizers.[80]

Given that intervallic and harmonic analysis in regard to tone systems and tunings is necessary,[81] and prerequisite to actually tuning an instrument (like for example a harpsichord) as well as to the performance of music, one could speak of a ‘primacy’ of music theory over practice. Such a point of view, which has been expressed by musically active theorists (from Zarlino to Karg-Elert) as well as by musicologists,[82] may be disliked by those who believe music theory should stick to a descriptive and hermeneutic orientation rather than being ‘regulative’ in whatever way. One should bear in mind, though, that the very notion of ‘theory’ implies a claim to truth and validity besides objectivity and methodological coherence. Therefore, ‘music theory’ cannot abstain from such claims that are basic to all science. Moreover, music theory, beginning perhaps in the Renaissance era, often included a developmental momentum in that theorists designed systemic features and techniques they thought could or should be relevant for contemporary as well as for future composers when creating music.[83] Their approach thus was prospective rather than retrospective.

3.2 Rameau, ‘physicalism,’ and the minor tonality

Rameau has been criticized, more than once, for having introduced ‘physicalism’ into music theory[84] when trying to base his view of harmony on findings reported from acoustical investigations Sauveur and others had carried out on vibrating strings. Any critical examination of Rameau’s approach to harmony should take into account that, by about 1700–1720, research into acoustics and also matters pertaining to auditory perception had been done for almost 200 years.[85] For example, the phenomenon of resonance was certainly known since about 1500–1530, and in the 17^th century there were various instruments in use employing sympathetic strings such as the ‘trompette marine’ and the viola d’amore.[86] Acoustic production of harmonics had come massively into play already around 1500 when organ building in many regions had begun to involve reed pipe stops plus compound mixture stops such as ‘Régale,’ ‘Dulzian’ and ‘Krummhorn,’ on the one hand, and ‘Zimbel,’ ‘Fourniture’ or ‘Scharf,’ on the other.[87] Werckmeister explicitly names the odd harmonics that can be produced by overblowing a stopped flue pipe.[88]

At the time Rameau was writing the Traité, various publications dealing with acoustics and sensation had become available. In regard to France, one of course thinks of Mersenne’s[89] and Sauveur’s writings. Rameau’s Traité still refers to string divisions and proportions (as was customary[90]); acoustics do not yet play a major role (there is the occasional observation, e.g. overblowing a flute into the octave “ne dépend que la force du vent”). However, Rameau points to the fact that string divisions lead to harmonic ratios representing perfect major (“… la corde entiere, qui renferme dans ses premieres divisons, des consonances qui toutes ensemble forment une Harmonie parfaite” (namely octave, fifth and major third).[91] By 1701, Sauveur had published a comprehensive treatise on scales, intervals, and tuning that probably stems from a series of lectures he had delivered to the Académie Royale, in 1696–97.[92] In this treatise, aptly titled Système général des intervalles des sons …, Sauveur points to harmonics as found in string vibration but also relevant to explain the scale of tones available on natural horns (e.g., the cor du chasse).

As has been discussed elsewhere,[93] Rameau may have been informed about Sauveur’s work by L. B. Castel before writing his Nouveau système de musique théorique … (1726); in this book, Sauveur is quoted in particular in regard to aspects of tuning. From 1726 on, and clearly in the Génération harmonique (1737), Rameau had absorbed some of the subject matter discussed in the up-and-coming field of acoustics, and had made use of it for music theory. Parallels between the harmonic ratios of tones making up a major chord, and a series of harmonic partials as found in a single vibrating string are all too obvious. Both will give rise to a sensation of consonance (though the quality may vary somehow). A single thin brass string of a harpsichord when plucked contains many harmonics. The spectrum (Figure 4) taken from the sound of the lowest string of a French harpsichord[94] offers no less than 19 strong harmonics in the frequency range from 50 Hz to 1 kHz. A trained musician like Rameau, when analyzing the sound radiated from such an instrument, may well detect a number of the low harmonics that can be resolved by the ear:

Figure 4. Spectrum, sound of the note/string C, Pigalle harpsichord (1771)

Rameau’s view of harmony, based on his own experience as a musician as well as on findings reported by Sauveur, was by no means unreasonable. The fact that a series of harmonics (as observed in a vibrating string) results in a sound which listeners experience as consonant, follows from the spectral harmonicity, which in turn implies strict periodicity of the sound signal in the time domain. This in turn results in a periodic neural excitation pattern, which, finally, results in a sensation of consonance.[95] Of course, Rameau could not know all these interrelations then. However, one should accept that the ‘Physicalism’ introduced into music theory by Rameau and others (among them Mersenne, Huygens and Tartini) had an objective basis, on the one hand, and did fit into contemporary scientific discovery, on the other. The criticism levelled against Rameau and the “Obertönler” (as Handschin used to call them) in this respect seems disproportionate.[96] Moreover, there have been attempts recently to give music theory not only mathematical but also psychoacoustical foundations.[97] In particular the concept of consonance has been elaborated from this perspective,[98] in which some of Rameau’s ideas have been taken up and given a more formal as well as empirical treatment.

The problem Rameau and legions of later music theorists were faced with is the minor tonality, for which no easy acoustical explanation is at hand.[99] One of the remedies Rameau employed (and continued to put forward even in his late works[100]), is a symmetrical scheme of “aliquotes ou sous-multiples” and “aliquantes ou multiples.” Central to Rameau’s considerations is a symmetry between the harmonic proportion 1:1/3:1/5, and the arithmetic proportion 1:3:5. Basic intervals derived from the proportions 30:24:20 and 30:25:20 (Rameau 1726, 21) yield the major and the minor chord, defined by their “Son fondamental, Quinte, Tierce majeure & mineure.” Rameau, to be sure, considers the two thirds to have equal weight since to him the pure fifth and the two thirds are “Consonances premieres & directes.” Their counterparts, “la Quarte, la Sixte mineure & la majeure,” he labels “indirectes ou renversées.” (The term “renversement” is used by Rameau also with respect to inversions of chords). Assuming ‘octave equivalence’ because “… un son quelconque est toujours sous-entendu dans son octave …,”[101] and applying further a reduction whereby intervals are all put into one octave (instead of the three needed to locate these intervals on a single string[102]), Rameau developed a neat scheme of the musical scale as well as of the intervals constitutive for harmony. However, whereas the harmonic proportion actually fits the frequency ratios of partials in a string or air column (and hence can be regarded as given by nature), the arithmetic proportion, which may also be applied to the division of a string, normally will not result in ‘sub-harmonics’ (see below). It was during the 18^th century that string vibration was investigated from both a mathematical and experimental perspective; the results demonstrate that a string set to longitudinal and transversal vibrations produces a series of harmonics above a fundamental. Since the phenomenon of resonance was essential in both Sauveur’s and Rameau’s reasoning, and since the latter had employed the arithmetic proportion to establish the minor third (as well as the minor chord), one would have to see whether a string could resonate so as to produce those ‘aliquantes.’ Both Rameau[103] and d’Alembert[104] took pains to find at least faint ‘tremblements’ at the unison; Rameau had to admit, however, that there was no such acoustic support for harmonic minor as there was for major. This led him to conclude that harmonic minor, though basically on a par with harmonic major, is not just as natural as major, on the one hand, but – provided one follows Rameau’s derivation – offers many options, on the other (“… le mineur y sera susceptible d’une bien plus grande variété que le majeur”).[105] The other aspect suited to connect a major chord to its parallel minor according to Rameau is that they have two tones in common (“… le générateur du majeur, & sa tierce, forment la Tierce & et la Quinte du générateur du mineur …”). A similar argument, to be sure, was brought forward by Helmholtz when he said that chords are closely related to each other if they have one or even two tones in common (for example, C-major = c-e-g and a-minor = a-c-e).[106]

3.3 Rameau to Riemann: the emergence of ‘harmonic dualism’

One has to see that particularly the fundamentals of Rameau’s theory of harmony are close to what later, in the 19^th century, emerged as ‘harmonic dualism.’ Since this term nowadays is treated by some as if standing for an obsolete “attempt to answer a question that no longer interests us,”[107] it seems necessary to reconstruct basic considerations that led to ‘harmonic dualism.’ Perhaps the most basic, and one certainly still of interest to musicology, is that music theorists for centuries struggled to ‘explain’ harmonic minor (and the minor tonality in general) as a tonal and perceptual framework that differs in certain respects from major. Harmonic minor is found in so many works of the 17^th and early 18^th centuries, respectively, that theorists had to deal with minor chords and the minor tonality in a reasonable way. In general, theorists[108] elaborated on musically usable consonant and dissonant intervals before discussing chords and chord progressions.[109] Mattheson relates seven diatonic “Klang-Stuffen” (scale steps from d’ to c’’) to ‘Tonarten’ in that he proposes a symmetrical construct, which results in minor thirds above d’, e’, a’, and b’, and major thirds above f’, g’ and c’’.[110] If one adds, in addition to the major or minor thirds, a fifth to each of the diatonic “Klang-Stuffen,” the three major chords of c, f and g would form a cadence in major, and the minor chords of a, d and e correspondingly a minor cadence. Mattheson believed that there is a ‘natural order’ according to which a “soft” or, alternatively, a “hard” third must be assigned to a given diatonic scale tone (one obvious reason is to avoid accidentals and alterations).

Tartini (1754), one of the pioneers in research on combination tones, saw that the minor tonality was cumbersome to derive from the series of harmonic partials, and also less coherent than major when viewed from the combination tone perspective. His solution, based on elaborate geometric operations, indeed leads to a minor chord, in which the tones C-E^b-G-c stand in the relation 12:10:8:6.[111] The minor third of course is the arithmetic mean of the tones C and G, that is, Tartini applies an arithmetic division to the fifth to yield the minor third (and a harmonic division to obtain the major third). Though Tartini’s approach (based on two geometric figures: the ‘harmonic’ circle and the ‘arithmetic’ square) is his own, it reminds of Zarlino (and also of Rameau) since the harmonic and the arithmetic division of the fifth finally yield the major and the minor chord, respectively.

Zarlino had discussed arithmetic and harmonic division of intervals, which can be ordered in reciprocal series.[112] In c. 31 of the third part of his Istitutioni, he dwelled on how musical intervals could be combined in settings comprising several voices.[113] He gave a description saying that the range of concords not only consists of consonant intervals (forming two voices), but also depends on the position “… di una chorda mezana, che si pone tra la Quinta nella compositione.”[114] The third voice or string that lies within a fifth divides this interval in two possible ways, in that it is either divided “… o mediatione Arithmetica or alla mediocrità Harmonica; & da questa varietà dipende tutta la diversità, e la perfettione delle Harmonie …” Though one may dispute the exact meaning of certain words or even of parts of phrases found in this chapter, it seems clear that Zarlino saw the major and minor third as effecting and representing the harmonic and arithmetic division, respectively.[115] Zarlino further distinguishes the two thirds with respect to the affective power of music as serene (‘allegra’) and sad (‘mesta’), respectively.

Riemann, translating and interpreting Parte II, c. 31 as well as some related paragraphs of the Istitutioni,[116] and pointing also to chapters of the Dimostrazioni harmoniche (1571), came to the conclusion that Zarlino, by employing the harmonic and the arithmetic progression to form the relevant intervals, had at the same time determined the major and the minor chord as the two fundamental harmonic elements. Riemann’s interpretation has been questioned by Dahlhaus (1957) who showed that Riemann’s translation does not exactly match Zarlino’s text. In fact, there are some debatable sentences (including gaps) in the translation Riemann provided; seeing an important historical source for ‘harmonic dualism,’ he apparently strived to render an interpretation of Zarlino’s statements consistent with his own view. Though Riemann’s reading of Zarlino may fall short of philological exactness,[117] it would be unjust to denounce his translation as perfunctory, or even fabricated. Zarlino apparently distinguished the major and the minor genus according to the two progressions (see above) that resurfaced so prominently in Rameau’s writings. Rameau in fact was expanding on Zarlino (notwithstanding harsh criticism found in Rameau 1722) when using the harmonic and arithmetic progression as a mathematical (that is, ‘symbolic’) approach to the generation of musical intervals. However, Rameau also saw the reciprocal series derived from the respective proportions as a physical model until he became aware, around 1749/50, that a generation of the minor triad from acoustical principles was difficult to develop, and that the arithmetic progression applied to string lengths could not be employed along with theories of sympathetic resonance in a useful way.[118]

In principle, Rameau had set up a ‘dualistic’ theory of harmony notwithstanding the problems mentioned. Harmony became a central area of music theory consequent to developments in music that led to writing homophonic textures where the ‘vertical’ dimension grew almost independent of the ‘horizontal.’ Of course, there is always an interplay between voice-leading (voicing) and chord progressions, but even prominent music theorists have tended to focus on one of the two dimensions, with a relative neglect of the other.[119] The theory of ‘harmonic dualism’ does not assume that the ‘vertical’ dimension of chords and chord progressions can be modelled and analyzed without regard for voice-leading; however, in harmony (as treated in Riemann 1893, Karg-Elert 1930) and in ‘harmonic analysis’ (as explained in Vogel 1975, 1984, 1993) chords and chord progressions are usually given more weight than are aspects of voice-leading and melody.[120]

After Rameau had attempted to build harmony on acoustic foundations, Hauptmann (1853) took a different approach, in which acoustics played but a small role; there is the occasional hint to the “natural unlimited series of tones ordered according to ratios of vibration,”[121] but Hauptmann pursues rational musical discourse rather than scientific demonstration.[122] There are speculative ideas in Hauptmann due to his dialectic constructs, however, he tries to qualify his approach as logical and ‘natural’ because of corresponding to human apperception.[123] Hence Hauptmann believed he could claim that there are three, and only three ‘directly apprehensible intervals’ (octave, pure fifth, (major) third).[124] The same basic intervals occurred in Rameau, however, for acoustical reasons. Hauptmann shared some of Rameau’s ideas concerning the minor tonality (namely that a major chord and its parallel minor have two tones in common), and there is also the distinction of a tone “having” a third and a fifth, and a tone that “is” either a major third or a fifth.[125] The difference between ‘having’ and ‘being’ (German: Sein und Haben) rose to prominence in von Oettingen’s dualistic approach in defining major and minor chords relative to the structure and weight of their harmonic partials.[126] Oettingen (1904), in describing harmonic analysis and synthesis of partials to explain the principles of ‘Tonicität’ and ‘Phonicität,’ respectively, put the terms back on their feet, so to speak, when demonstrating that the acoustic and perceptional coherence of a pure minor chord is by no means inferior to that of a major chord since in both there are partials coinciding in frequency as well as partials with frequencies an octave apart. Coinciding partials as well as the marked periodicity of the resulting waveshape are acoustical correlates to a percept characterized as ‘Verschmelzung.’[127] Oettingen’s considerations, which combine some of the acoustical analyses of Helmholtz with psychological inferences given by Stumpf (1898), can be summed up in a table. For each tone in a pure major and its parallel pure minor chord, partials 1 – 10 are considered (Oettingen’s own concept did span four octaves):

Table 2. Acoustical structure of a pure major and its parallel minor chord

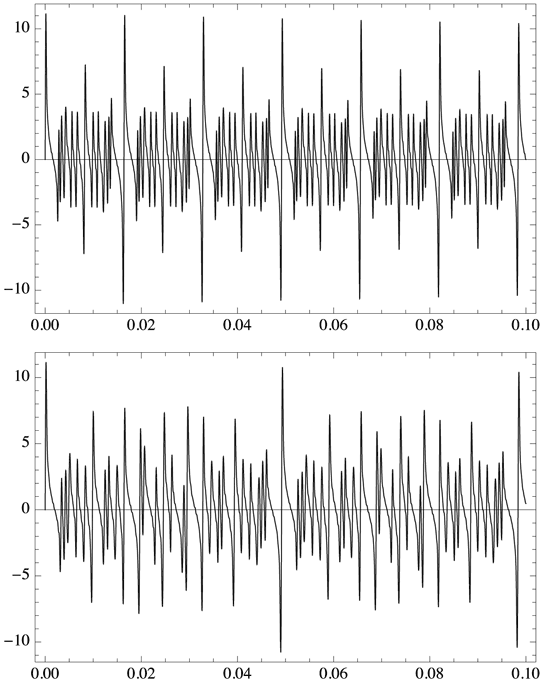
Taking into account chords composed in this manner (table 2), and applying pitch relations in just intonation (as is mandatory according to the concepts of Hauptmann, Helmholtz, Oettingen, Riemann, and also Stumpf), it is straightforward to synthesize such chords that, given their temporal and spectral composition, will result in highly ‘harmonic’ percepts since in particular the pure major chord exhibits spectral fusion that translates into a strictly periodic wavetrain where the period is clearly determined by the common denominator of the fundamental frequencies of the three complex tones forming a chord. Since, in our example, these frequencies are {244, 305, 366 Hz} = 4:5:6, it follows that f0 = 61 Hz, and T = 1/f ≈ 16.4ms[128]. Hence, the major chord is perceptually reinforced by a virtual pitch that can be taken as a ‘basse fondamentale.’[129]

Figure 5. Synthesis of C-major (upper) and a-minor chord (lower), ten partials per note (= 30 spectral components per chord), resulting waveshapes for t = 0.1 seconds

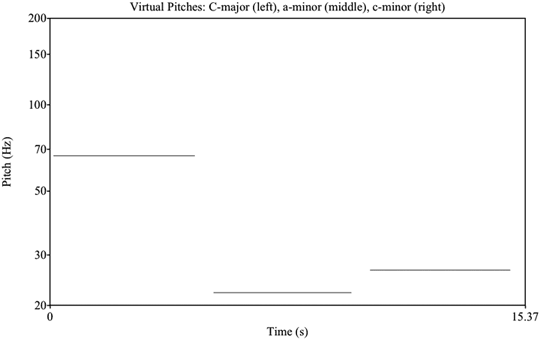
For the a-minor chord whose complex tones have fundamental frequencies at {203.333, 244, 305 Hz}, the appropriate virtual pitch is not just as easy to determine.[130] By calculation and measurement,[131] one can estimate a virtual pitch just above 20 Hz. Similarly, a c-minor chord with fundamental frequencies of {244, 292.8, 305 Hz} yields a virtual pitch at ca. 25 Hz. The virtual pitches found for the major and the two minor chords might be of different salience.[132]

Figure 6. Virtual pitches found by autocorrelation algorithm for the C-major, the a-minor and the c-minor chord (61, 20, 25 Hz)

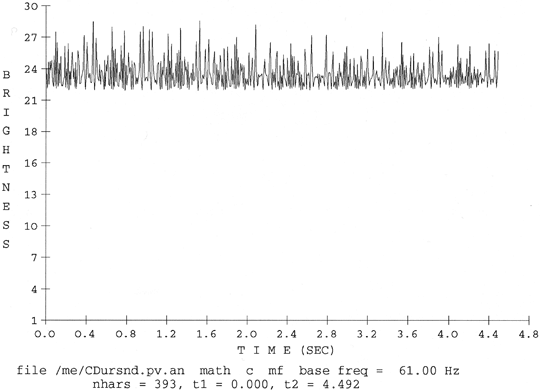
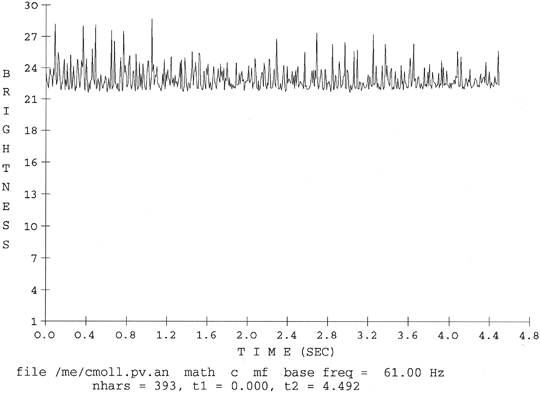
From these examples, it can be inferred that the difference between a major and a minor chord (realized in just intonation, and in ‘root’ position) is that the minor chord is likely to evoke a somewhat weaker low virtual pitch. With respect to another relevant perceptual feature, spectral brightness, major and minor chord based on identical fundamental frequency differ but little. For the C-major and the c-minor chord used as examples, the average spectral centroid is ca. 1550 Hz and ca. 1500 Hz, respectively. Normalized spectral centroid gives the brightness of a sound; as figures 7a/b demonstrate, both chords are almost identical in brightness.[133] This result does not support the commonly held view according to which a chord in minor is just the muddy variant of its major prototype.

Figure 7. Brightness of a C-major and a c-minor chord, fundamental frequency = 244 Hz

In the light of the empirical data complementing theoretical considerations, Oettingen was certainly on the right track when he expressed the need to deal with harmonic minor as a phenomenon that cannot be simply taken as ‘blurred major’ (“getrübtes Dur,” as Helmholtz, Hindemith and others saw it). Oettingen took great pains to reinstall music theory on a basis provided by musical acoustics and psychoacoustics.[134] To this aim, he developed special signatures indicating tone relations (that can be traced by means of a two-dimensional tone net), and he also conducted many experiments where listeners were requested to judge chordal patterns played in several intonation variants. For these experiments, he employed a special harmonium (the ‘Orthotonophonium’[135]) that offered 53 notes per octave (in another version, even 72 notes per octave). Oettingen’s approach included empirical work along with theoretical argument; he devised a coherent and systematic treatment of harmony based on a strictly dualistic perspective (which led him to make the note d the central note for both the tonic and the phonic chord[136]).

When Riemann, in 1874, began to publish on music theory, he could draw from Hauptmann (1853), Oettingen (1866), and Helmholtz (1863), as he in fact did in various contexts (approving as well as contradicting points of view issued by his masters).[137] For a time, he admired also Stumpf for his Tonpsychologie (1883/1890), and in particular for the concept of ‘Verschmelzung’ that is at the core of Stumpf’s theory of consonance (1898).[138] Since it is not possible, at this place, to reconstruct Riemann’s theoretical concepts in any detail (which he, moreover, changed considerably in the course of more than four decades he remained active as a musicologist and author), we could simply point to Riemann’s account of the history of music theory where he, at the very end, states that this book should be regarded, in particular in its third part (titled “Die Harmonielehre,” Chapters 14–16), as a “Rechenschaftsbericht über die Herkunft meiner Ideen zur Theorie der Musik.”[139] Indeed, Riemann saw himself as completing what Zarlino had begun, and what Rameau, Hauptmann, Oettingen, Helmholtz and others had tried to achieve: to ground music theory, and, most of all, harmony, on a firm, scientifically proven fundament. This fundament, however, did undergo significant changes in the course of Riemann’s scientific career. He started with a perspective on ‘Musikalische Logik’ as outlined by Hauptmann (on the basis of ‘harmonic dualism’ and just intonation), but soon sought to integrate psychoacoustics of pitch, interval and chord perception as provided by Helmholtz. In certain respects, Oettingen offered a combination of both since he took acoustics into account (without overstretching acoustical principles and facts), and also saw the need to investigate the relationship (‘Verwandtschaft’) of chords from the point of musical perception and apperception. By the time Riemann wrote his dissertation under the guidance of Hermann Lotze (a physician and philosopher by academic training), he aimed at a (in modern terminology) ‘transdisciplinary’ approach to the study of music perception.[140] There are indications that Riemann sought to cooperate with scholars of the ranks of Helmholtz and Oettingen, for example, in clarifying the matter of audible undertones.[141] In certain respects, he fell victim to Helmholtz’ hypothesis according to which certain parts of the basilar membrane in the inner ear can be viewed as a system of parallel-wired mechanical resonators working like the strings of a piano.[142]

With the anatomical knowledge at hand around 1855 (Alfonso Marchese Corti had just discovered what became known as Corti’s organ), Helmholtz thought “… dass jedes solches Anhängselchen, ähnlich den Saiten des Claviers, auf einen Ton abgestimmt ist ….”[143] Riemann took up this resonance hypothesis, and even expanded it, in his doctoral dissertation[144] in order to find a reasonable explanation for the perception of harmonic minor. His claim was as follows: “… die den Untertönen eines angegebenen Tones entsprechenden Fasern der Membrana basilaris schwingen partiell mit und wir haben daher die Vorstellung der Untertöne implicite.” To be sure, Riemann did not argue that undertones were present in the soundwave; he infers that the inner ear mechanism (not well understood yet in 1873) would bring about a sensation of undertones only ‘implicite.’

Riemann’s various statements on undertones and resonance phenomena have been reiterated time and again, most often with the intention to discredit Riemann as well as harmonic dualism; the communis opinio is that if there are no undertones, there is no basis for dualism. Such a view is simplistic, though; neither did harmonic dualism as developed by Hauptmann and von Oettingen rest on assumptions which would require acoustically ‘real’ undertones, nor did dualistic concepts issued in the 20^th century by Karg-Elert (1930) and his pupils as well as by Martin Vogel (1975; 1993) who perhaps remained the scholar closest to Oettingen’s approach. Moreover, at least some of Riemann’s experiments have been misinterpreted in order to ridicule him (and thereby also harmonic dualism; the strategy is all too obvious). Riemann evidently did not begin his inquiry with some fallacious “moonshine experiment,”[145] but had worked with his harmonium he had tuned to produce intervals that gave rise to sensation of a virtual pitch or pitches below the fundamental frequencies of the tones played. His observations, which can be interpreted in regard to combination tones as well as the ‘missing fundamental’ (Schouten’s ‘residuum’) and subharmonic matching,[146] have been checked and accepted as valid.[147] It was probably from Helmholtz’ (1863) treatment of resonance phenomena that Riemann set out to conduct some experiments where he believed to have detected ‘undertones’ in vibrations of undamped piano strings.[148] Most critics have categorically denied that Riemann could have heard what he claimed to have heard; however, Carl Stumpf, who repeated Riemann’s experiments, came to the conclusion that Riemann in fact could have sensed certain sounds, which Stumpf attributed to the overall vibration pattern (“… allgemeine Erschütterung des Instruments …”) of the piano once set to motion.[149] Stumpf thought that Riemann was misled to take these sounds as ‘undertones.’ However, Stumpf found in some of his own experiments (simultaneously playing two strings of his violin) not only partial sympathetic vibration of the string tuned lower when bowing the string tuned higher, but also sympathetic vibration of the full string length when his bowing was strong. He concluded: “Wie leicht könnte man nun hieraus wieder auf die objective Existenz der Untertöne schließen!”

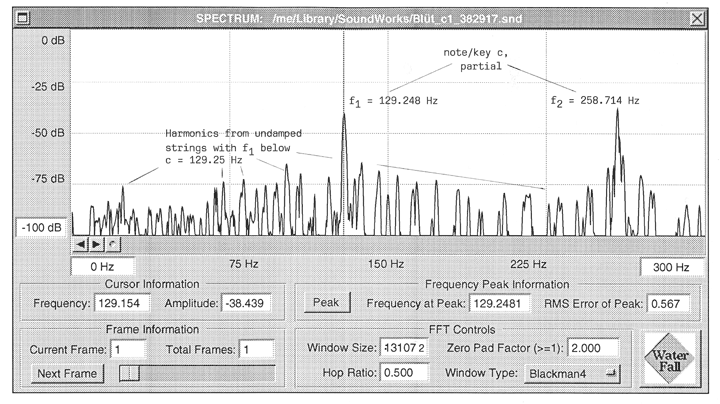
Apparently, things are not as simple as to dismiss the case altogether. If one repeats one of Riemann’s ‘moonshine’ experiments (familiar to musicians and musicologists), it gives some cues that might help to explain Riemann’s presumed sensations. In figure 8, the spectrum of a sound recorded from a Blüthner concert grand piano (280 cm) is shown.[150] The large peaks f₁ and f₂ at 129.25 and 258,71 Hz, respectively, are the first two harmonic partials of the note/tone c (C3) that was played while the keys C (C2) and C, (C1) had been pressed before, and the dampers had been lifted from all the strings. The spectrum obviously contains (a) considerable energy below f₁; among the many components is one about one octave below f₁. Also, there are (b) many components between f₁ and f₂ that are certainly not partials of the note c, which has been played, but partials of strings whose fundamental frequency is below that of the note c. Though the single string will not produce ‘undertones’ under normal conditions,[151] sympathetic resonance phenomena such as recorded from undamped strings in a piano may have led Riemann to believe that he had detected ‘undertones.’

Figure 8. Spectrum (LTAS), grand piano, note/tone c plus low spectral components

Riemann’s failure to see his experimental observations acknowledged went along with another disappointment; the cooperation he seems to have sought with scientists and psychologists like Helmholtz, Oettingen and Stumpf didn’t materialize. One can see how Riemann’s attitude changed from youthful enthusiasm as expressed in his dissertation and in the Musikalische Syntaxis (1877) to defence and disappointment as expressed in his series of articles on ‘harmonic dualism’ (1905). In between, probably realizing that Oettingen’s strict approach to dualism was difficult to reconcile with ordinary listeners’ experience, and even more so with contemporary musical practice based on the piano and equal temperament, Riemann worked out a compromise.[152] In essence, it asserted that harmonic dualism as well as just intonation is correct in theory, but not possible and not even needed in practice. This point of view is maintained in the Ideen zu einer Lehre von den Tonvorstellungen (1914–16). A central component of Riemann’s compromise that he presented in several publications (with updates and revisions) was his doctrine of ‘enharmonic identification;’ this notion turns up already in the Syntaxis (1877) and is elaborated in more detail in Das chromatische Tonsystem (1895). However, still in the Ideen the ‘enharmonische Identifikation’ is heralded as a new and groundbreaking concept Riemann promises to present in a detailed format in the future.[153] One can of course see what he meant by ‘enharmonische Identifikation’ as well as by a concept labelled ‘economy of imagining’ or conceiving (“Ökonomie des Vorstellens”).[154] Both would have needed detailed treatment since Riemann was calling for the most differentiated ‘Tonvorstellungen’ possible, on the one hand, and at the same time saw a need for reduction of such elaborate images as could arise from the multitude of tonal relations at hand in just intonation, on the other. ‘Economy of imagining/conceiving’ thus should regulate our ‘Tonvorstellungen’ in an effective way. However, elaboration and simplification can become conflicting strategies so that their possible interplay would have to be explained in a full-grown ‘Lehre von den Tonvorstellungen.’

Another simplification Riemann undertook concerned the two-dimensional Tonnetz. In Oettingen’s original publications,[155] the rectangular or quadratic tone-net relates eight tones to each center tone one may choose, namely the fifth below and above this tone, the major third above and below this tone, and the major third below and above the two fifths, respectively. Riemann had adopted this scheme while others had simplified it early on to six tone relations per centre tone.[156] In his Ideen, Riemann used the diamond-shaped tone-net that implies the reduced six-note format. It is this reduced format that has been adopted widely in “Neo-Riemannian” schools whereas Oettingen’s tone-net has been expanded into a three-dimensional structure incorporating tone relations based on prime numbers {3, 5, 7} by Vogel.[157]

Whereas Oettingen did strive to (re)unite music theory and science, Riemann’s compromise concept separated music theory from musical acoustics and psychoacoustics,[158] to the effect that music theory is not concerned with musical sound organized so as to realize tonal images (‘Tonvorstellungen,’ which are also a central part of Oettingen’s concept), but with tonal images conceived apart from actual sound and intonation patterns. Already in the Syntaxis, Riemann’s argument is set forth in regard to reading music and correct orthography (making use of ## and bb), a perspective maintained in the Ideen.[159] Riemann’s ‘Musikalische Logik’ was enough to secure correct understanding of musical structure, and of harmony in particular, notwithstanding abstruse deviations from just intonation pitch patterns that might occur in music performances. However, Riemann never gave up ‘harmonic dualism’ as a concept, nor did he relinquish just intonation as a theoretical reference system.[160] This alone gave rise to ardent resistance as expressed by Capellen (1905) and others who held that, from a ‘monistic’ perspective, there was but one ‘natural’ or logically possible way to perceive major and minor chords and other sonorities, namely from bottom upwards. From a phenomenological point of view, the position of the (ideal) listener in a two-dimensional tonal space has been identified with the base note of the (major and minor) triad. The argument is that this position is implied by the structural composition of triads (thirds piled up on a base note acting as an anchor) as well as by our listening experience.[161] Such assertions of course can be, and should be tested empirically.

In regard to ‘bottom-up’ vs. ‘top-down’ perception of vertical chordal structures, it has often been argued that the bottom-up adjustment would also apply to triads in a minor key, in particular if such are in root-position. According to a prediction model, perceptual roots of root-position diatonic triads in a minor key lie in the bass.[162] Parncutt points to investigations of Bach chorales,[163] though, where it was found that the soprano voice is doubled more often than the bass.[164] Hence, “the soprano voice is a root candidate by virtue of its voicing alone, consistent with the idea that the soprano and the bass are the most perceptually salient voices in a four-part texture (presumably due to relative lack of masking by other voices).”

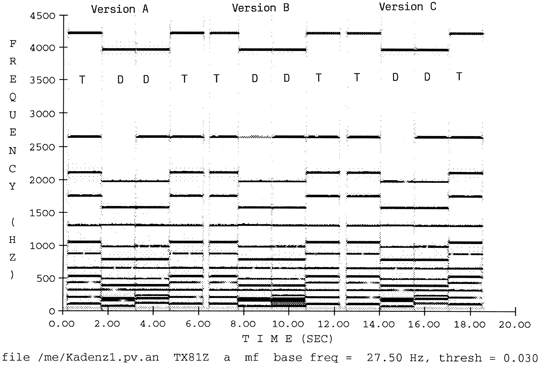
The ‘bottom-up’ orientation in regard to perception of chordal structures may in fact be not as ‘natural’ or ‘logical’ as it is for major chords in root position because of psychoacoustic implications.[165] For example, in a (preliminary) experiment, twenty-one musically trained subjects were asked to judge four (complete or abridged) cadences played in minor keys on two variables: (a) harmonic coherence and (b) musical conclusiveness. The judgements were done on a scale from 1 = very low to 7 = very high. The cadences were taken from Riemann (1893) and other textbooks on harmony, and recorded with two synthesizers (Yamaha TX 81 Z) in just intonation tuning. Each cadence was presented (A) in original form, (B) with one voice added in the bass, and (C) one voice added on top of the soprano. To avoid marked shifts in spectral brightness, these additional voices were recorded -8dB below the level of the main 4-part texture. The resulting sound pattern for cadence no. 1 is shown in figure 9.[166] The relative shift of the spectral centroid over time is documented in figure 10.

Figure 9. Cadence °T-°D, °D-°T (a-minor = e-Unterklang), three versions A, B, C

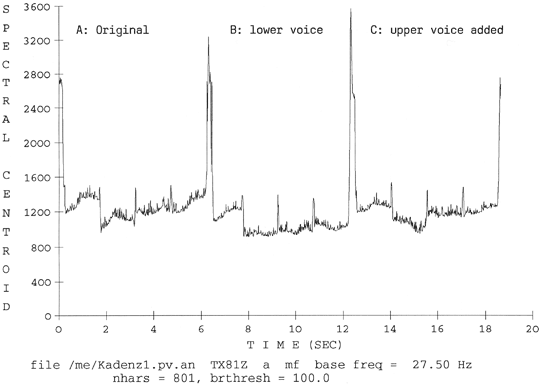
Figure 10. Spectral centroid./.time of cadence (versions A, B, C)

From figure 10 it is evident that adding a voice in the bass even at a reduced level adds to the ‘bottom end’ of the chord acoustically; moreover, the bass part is reinforced musically. This might lead to subjects’ judgement expressing at least a relative preference of this version (B) over the other two (A, C). The actual ratings, however, did not exhibit significant differences for the three versions:[167]

Table 3. Descriptives, cadence 1, (a) harmonic coherence, (b) musical conclusiveness, n=21

Correlations between data (samples/files 1–6) show that the judgements are consistent within and between the two variables (r_xy ranges from r₂₄ = 0.472, p = 0.031 to r₁₃ = 0.781, p < 0.001). The only correlation that is not significant is r₂₆ for musical conclusiveness between the original version (A) and version (C). After homogeneity of variance between samples had been checked with Bartlett-tests, ANOVA was performed where the versions A-C were taken as treatments of the factor ‘cadence.’ ANOVA gave no significant results. Neither did the six mean values (aM) subjected to a multiple-mean test (Scheffé) give any significant contrasts. Hence, the three versions seem to appear quite similar to listeners. Interestingly, version (B), which gained a little in harmonic coherence by adding a voice to the bottom, loses as much against the other two versions in conclusiveness.

Taking the data from five treatments, average ratings in general increased from the original (A) to versions (B, C) on both variables when either an additional voice below the bass or above the soprano were offered. Also, ratings increased when in one complete I-IV-I-V-I cadence a supporting voice was added, in the same sound stimulus, below the bass and another one above the soprano voice.

These findings, restricted as they are, at least do not support the assumption that listening attitude in regard to chords and chord progressions is always and invariably ‘bottom-up’ and centred at the bass. This is not to say that Oettingen’s ‘top-down’ approach to ‘Unterklänge’ would duly apply. Rather, depending on musical context and, evidently, on the musical expertise of a listener trained to work out advanced ‘Tonvorstellungen,’ chord progressions can be apprehended in ways incorporating ‘harmonic dualism.’[168] As with many things, this is a matter of training and experience.[169]

The problem with ‘harmonic dualism’ is not that certain chords are conceived as ‘Unterklänge’ (as such in fact can be found in works of Wagner and other composers). A serious problem seems to be that, whereas in harmonic major the base note (Grundton) of a chord in ‘root position’ is also the note from where all tonal relations are the most simple ones (4:5:6), in harmonic minor the fifth must be chosen as ‘anchor’ (Bezugston) to derive the same simple proportions implied by Riemann’s ‘Ökonomie des Hörens.’[170] Consequently, a simple strategy of perceiving the ‘Grundton’ also as a cognitive anchor point would be missed in harmonic minor. In certain works, or parts thereof, listeners would be forced, in a strict dualistic approach, to shift between anchor points identified with the base note (for major chords), and the fifth (for minor chords). Consider, for example, bars 31–34 of Bach’s Fantasia et Fuga in g (BWV 542). The chord progression is as follows (uppercase letters = Major chords; lowercase letters = minor chords):

D-g-G-c-C-f-F-b^b-B^b-e^b-E^b-a^b-A^b-d^b-D^b-(diminished chords, bar 35)-e (bar 36)

In this passage, Bach not only moves around the ‘Circle of Fifths’ (that had been given a formal description in Heinichen 1728), from D to D^b, but alternates regularly between major and minor chords of the same key. Viewed from a perspective of strict dualism, the consequence would be to change the ‘anchor note’ (base note, fifth) and the direction of perceiving chords (upwards in major, downwards in minor) as indicated above. This is what the ‘monists’ blamed as ‘unnatural’ and contradicting common experience.[171] The problem that a ‘Grundton’ (lowest note as played and heard) and a ‘Bezugston’ (center note of a chord defined by chord structure and harmonic function relevant to apprehension) might dissociate is not confined to harmonic minor, though, since inversions of major chords can bring about the same effect.

The degree of differentiation and exactitude musically trained subjects may achieve in regard to apprehending and conceptualizing tonal relations, of course varies according to certain objective and subjective factors. Apparently, advanced conceptualizations of intricate chord and key relationships as are found in many works of the 19^th and early 20^th century, can be developed by intensive training including listening, performance, and analysis. This is what Riemann understood by ‘Musikalische Logik,’ and what he still proposed in the Ideen. His own work, impressive as it is, would certainly have benefited from empirical investigations relevant to music perception and cognition. Riemann was lacking support from psychologists and acousticians, and he may have been too idiosyncratic to cooperate in a team (should such an opportunity have existed). Oettingen, by contrast, notwithstanding his strong theoretical claims, was more of an empiricist,[172] and carried out experiments on perception of major and minor chords (including aspects of tuning and intonation[173]). This, however, was only possible in the last years of his life (after he had access to a special ‘Reinharmonium’ making different intonation patterns possible). Systematic research in areas of perception and cognition relevant to music theory remained scarce for decades to come.

4. Conclusion: Theory, ‘Handwerkslehre,’ Empirical Research

Music theory, since antiquity, combined rational analysis and speculation (as expressed by the term ‘theoria’) with empirical investigations. This line of tradition can be traced well into the 20^th century[174] up to the present.[175] Already in the Renaissance and Baroque era, and parallel to more ‘scientific’ approaches to music theory (accentuating mathematical, acoustical and psychological aspects), description of musical structures with the goal of understanding as well as regulating actual composition gained ground. Whereas Zarlino (1558) strived to contribute to both areas, many later writers were concerned with fundamentals of ‘Tonsetzkunst,’ in the first place.[176] The shift of focus becomes obvious in works like Weber’s Versuch where, at the end of the introductory chapter that still offers some elementary musical acoustics, the author leaves no doubt that his main subject is “Theorie der Tonsetzkunst oder Tonsatzlehre”[177] needed to prepare for the “Practische Ausübung der Tonsetzkunst,” that is, musical composition.

‘Tonsatzlehre’ is what in fact is covered by ‘practical’ (or applied) music theory in many academic institutions. This field has been combined with music analysis in order to foster understanding of techniques of composition that were of importance in the past. Parallel and somewhat unconnected to such more or less ‘practical’ approaches, music theory in the 20^th century saw a broad range of theorizing often based on abstract (mathematical, logical, computational) considerations and models, covering such diverse things as set theory, information theory, statistical distributions and probability functions, fuzzy logic, etc. By about 1970, a reorientation took place (more or less parallel with the so-called ‘cognitive turn’ in psychology and adaptation of concepts from Gestalt psychology) in which also structural linguistics played an important part. After serialism, on the one hand, and aleatoric as well as similar ‘stochastic’ concepts, on the other, had failed to attract listeners in significant quantities, a new interest in foundations of tonal music viewed from a cognitive perspective awoke.[178] This perspective included experimental investigations as well as modelling of perceptual and cognitive processes, for example, by neural networks.[179] Only to sum up most of the relevant research that has been done in this area would require another article. It is enough, at this point, to indicate that there are many specialized publications reporting findings on specific problems (for example, concepts of ‘similarity’ as are relevant to music perception[180]).

Taking into account developments of the past decades, one can say that nowadays basically several camps coexist (and mingle with each other, at least to some extent), one devoted to historical and applied ‘Tonsatzlehre’ (either ‘practically’ inclined or with a focus on certain eras and styles), another anchored in conventional areas of music theory (with a Schenkerian or, growing in the 1990s, “Neo-Riemannian” orientation). Then there are music psychologists with an interest in music theory as well as theorists who contribute to the psychology of music,[181] not to forget investigations the neurosciences have done in music perception and cognition that also have implications for music theory.[182] In addition, one could point to artistic concepts (some of them again backed by scientific orientations, for instance, in computer music) proposed by composers or ‘media artists’ working in or with sound.

Given this broad range of directions, research activities, and methodologies, it may be difficult to determine a single field of ‘music theory.’ What can be said, though, is that major areas traditionally considered to make up the core of tonal music theory (harmony, melody, rhythm and meter, form structure) have been subjected more and more to empirical investigations, to the effect that music theory nowadays seems to be ‘rule-based’ rather than ‘dogmatic,’[183] whereby ‘rule-based’ refers to perceptual and cognitive processes actually observed, or assumed to exist in expert listeners.[184] All in all, empirical studies have been given much more weight over the past decades. At the same time, theoretical concepts from the past (like ‘harmonic dualism’ as well as concepts of Tonnetz and ‘tonal space’ as explored by Oettingen, Fokker, Vogel, etc.) have been revitalized, and given new interpretations.[185] One of the tasks of systematic musicology is to contribute to empirical research relevant to substantiate music theory; another is to examine theories, models and empirical findings as they become available from various areas of research with the objective to seek coherent and causal explanations of musical phenomena.