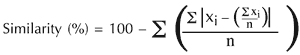Zygonic Theory: Introduction, Scope, and Prospects
Adam Ockelford
This extended article introduces Adam Ockelford’s ‘zygonic’ theory of music-structural understanding, which holds that imitation, which can occur in all domains of perceived sound and at all levels, is the ultimate organising force in music. Hence the theory is potentially of value not only in theoretical terms (shown here in relation to the first movement of Mozart’s Piano Sonata K. 333), but metatheoretically too, as a tool to interrogate other systems of musical analysis (an example is provided in relation to Allan Forte’s ‘set-theoretical’ method). The zygonic approach also enables the powers of influence at work in group improvisation to be captured, permitting the evolution of musical ideas to be charted as they unfold in time between performers, and a zygonic analysis of a short, improvised song with piano accompaniment is provided by way of illustration. Finally, zygonic theory prospectively offers an epistemological link between the sister (though sometimes apparently incompatible) disciplines of music psychology and music theory – an avenue that is explored briefly in conclusion.
1. Preamble
Although it was not named as such for some years afterwards, zygonic theory was born in 1983 when, as a young composer, I was interested to see whether some of the techniques of serialism, with which I had been experimenting as a composition student at the Royal Academy of Music in London, could be made more generally accessible to listeners. Would it be possible to adapt Arnold Schönberg’s original ideas to work within what I thought of as the ‘musical vernacular’ – the broadly accepted notion of tonality with which Western listeners are implicitly familiar? This line of thought led naturally to a review of the rather more venerable principles of canonic writing. Could the ancient notion of imitation be fused with the more recent invention of serialism to create musical structures that would appeal both on a conceptual level to those attending with an analytical mindset and to ‘everyday’ listeners, for whom an unwitting grasp of the music’s organisation may intuitively give a sense of aesthetic satisfaction?
The result was a series of choral folksong arrangements, which, while adhering to the traditional principles of Western tonal harmony, nonetheless used a combination of advanced contrapuntal and neo-serial techniques. Here, for example, is an excerpt from an unpublished nine-part setting of the British folksong O Waly, Waly. The tune is placed in the middle of the accompanying texture, which comprises vocal lines made up entirely of three-note melodic cells, derived from the climax of O Waly, Waly – ‘A, 
Figure 1. Vocal arrangement of O Waly, Waly (Ockelford 1983).
Although I felt that this arrangement of O Waly, Waly succeeded in the sense of imbuing an easily digestible tonal texture with strict intellectual coherence, I soon discovered that unless the structural niceties that I had so painstakingly fashioned were pointed out to listeners – even to fellow musicians – they passed by unnoticed. If asked what struck them about the passage in question (Figure 1), people usually made a response in relation to the richness of the chromatic harmonies. Now, it may or may not have been the case that the strict organisation in the domain of pitch gave the music a particular feeling of unity that was perceived nonconsciously; there was no way of telling. But in any case, it was clear that this was not the principal form of musical structure that was in play from a perceptual point of view. Listeners’ reactions suggested that the arrangement of O Waly, Waly made sense – and had an emotional impact – quite irrespective of its neo-serial and canonic convolutions.[2] Evidently, then, there must have been other, more fundamental, kinds of structure present, which I had used unwittingly and which listeners, irrespective of their level of musical expertise, were intuitively able to grasp. I was curious to know what these properties were and just how they worked.
This was a problem, though, to which no answer was immediately apparent. So I took a step back and reflected upon those structural aspects that I had devised and of which, therefore, I felt I had some understanding. The neo-serial and canonic techniques had a common element – imitation – and it occurred to me that when one musical feature was created by imitating another, then, to the musical mind that recognised the replication, it was as though the first metaphorically exerted some form of control over second. From my (the composer’s) point of view, to whom all manner of sounds had theoretically been conceivable when arranging O Waly, Waly, it seemed, in retrospect, that imitation had given me a way of bringing order to the theoretically infinite sonic palette from which I had been free to make choices.
When listening to the music, it was clear that imitation was the vehicle that drove musical logic and coherence at the motivic and thematic levels, but it did not appear to be applicable to other aspects of the piece. What about those chromatic harmonies, for example, to which listeners had referred upon encountering my arrangement of O Waly, Waly? Was it possible that imitation was somehow at work in relation to these and other musical elements too? Perhaps. But how, I could not imagine.
My train of thought having reached a cul-de-sac, I turned for inspiration to the music-theoretical and analytical literature: not so much texts about counterpoint and serialism, whose structural mechanisms were (I thought) clear, but to other topics, including form, process, harmony and tonality. Here, there was relatively little mention of imitation per se, but an almost universal recognition of the part played by a closely related concept: repetition.
The traditional notion of musical form, for example, as espoused by writers ranging from Stewart Macpherson (1915) to Wallace Berry (1966 – subsequently re-issued in 1986), with its notion of stereotyped structures such as AA'A''A''' … (characteristic of variation sets), ABA (‘ternary’ form) and ABACA … (the ‘rondo’), implicates repetition both within pieces and between them. It was also evident that repetition is central to the various motivic-cum-thematic theories that have been propounded, in whose development the music and writings of Schönberg have proved seminal. His ideas were taken to their logical extreme by a one-time pupil, Rudolph Réti (1951), who demonstrated, to his own satisfaction at least, that many works from the Western classical repertoire are each built on a single theme, surface contrasts notwithstanding. In his early treatise on harmony (1906), Heinrich Schenker also acknowledged the part played by repetition, not only at the level of motives, but in the construction of large-scale forms as well. This recognition carries over into the sophisticated models of musical structure that followed; in Der Freie Satz of 1935, the question of repetition at deeper structural levels is aired in some detail. But of greater significance to my enquiry was the fact that repetition underpins the symmetries within the Ursatz, the harmonic-melodic framework that Schenker considered to underlie all tonal masterpieces.
Turning to the oeuvre of Leonard Meyer, it became apparent that his evolving reflections on musical patterning (1956, 1967, 1973) variously involve repetition, most overtly in his notion of ‘conformant relationships’, ‘in which one (more or less) identifiable, discrete musical event is related to another such event by similarity’.[3] Although it is not stated openly, the concept is no less important, however, in the first chapter of Music, the Arts, and Ideas (1967), where the author’s previously developed model of musical meaning is reviewed in the light of information theory.[4] Meyer’s thesis is this: for experienced listeners, an incomplete portion of music implies certain continuations, which vary in probability according to the frequency of past occurrence (hence the significance of repetition). It is, Meyer asserts, deviations from the expected course of events that give rise to musical meaning. Moreover, Meyer identifies a number of different basic melodic structures (subsequently termed ‘processes’ by Burton Rosner and Meyer in 1986), including conjunct, disjunct and symmetrical patterns, whose internal regularity and use as stylistic archetypes imply repetition within and between works.
I found that other models of musical structure, reflecting a range of approaches, variously involve repetition too, such as Herbert Simon and Richard Sumner’s (1968) system of encoding patterns parsimoniously using preordained ‘alphabets’ and the operators ‘same’ and ‘next’; set-theoretical analysis, which entails abstracting groups of pitch-classes and tracing similarities between them (initially set out by Allen Forte in 1973 and comprehensively reviewed in Music Analysis 17, 1998); and semiological analysis, to which motivic similarities are fundamental.[5] As Nicolas Ruwet says: “I shall start from the empirical appreciation of the enormous role played in music, at all levels, by repetition, and I shall try to develop an idea proposed by Gilbert Rouget: ‘… certain fragments are repeated, others are not; it is on repetition – or absence of repetition – that our segmentation is based’”.[6] Finally, I came to appreciate that repetition (‘parallelism’) accounts for four of the five preference rules underlying Fred Lerdahl and Ray Jackendoff’s A Generative Theory of Tonal Music (1983) – GPR 6, MPR 1, TSRPR 4 and PRPR 5 – as well as being implicit in a number of others, such as GPR 5 (symmetry), for example. As the authors state: “The importance of parallelism in musical structure cannot be overestimated. The more parallelism one can detect, the more internally coherent an analysis becomes, and the less independent information must be processed and retained in hearing and remembering a piece.” [7]
Mulling over the strands in this rich tapestry of musicological thought, it seemed that, while repetition (and, by implication, imitation) had been discovered, recorded and analysed using a number of different methodologies in relation to chunks of music, which were the length of motives or longer (phrases, themes and sections; see Schönberg 1967),[8] no one had thought to peer down the other end of the telescope, as it were, and systematically investigate repetition on a smaller scale, where individual notes were taken to be the fundamental units of musical construction. To see where this thinking might lead, I mentally ran through the simplest tune that came to mind, the English nursery rhyme Twinkle, Twinkle, Little Star[9] – see Figure 2.
Figure 2. Some different forms of repetition present in Twinkle, Twinkle, Little Star.
Adopting a ‘traditional’ analytical mindset, it was the exact repetition of phrases that immediately became apparent: lines 1 and 2 are reprised to form the conclusion of the song (lines 5 and 6), before which, in a short central section, line 4 echoes line 3. Hence the piece has a simple ternary construction: A B C C A B. Moreover, taking into account approximate repetition (in the form of transposition), it is evident that line 3 is a variant of line 2. Hence, the global structure of Twinkle, Twinkle can be expressed as: A B1 B2 B2 A B1. This is all perfectly straightforward. However, examining the statistics relating to individual notes, it was evident that my conventional account of the nursery rhyme’s structure by no means captured all the repetition that is present. Twinkle, Twinkle comprises six lines of seven notes, making a total of 42 distinct sonic events. Yet there are only nine different ones, as follows (see Figure 3).
Figure 3. Frequencies with which different notes occur in Twinkle, Twinkle, Little Star.
That is to say, Twinkle, Twinkle is saturated with repetition at the level of notes, with each appearing, on average, a little under five times. So it occurred to me that maybe it was the notes themselves that had been chosen in imitation of each other, and were intuitively perceived in this way. I listened again to the opening of the first line, and, reflecting on the experience, it became clear that I was hearing the second note – a repetition of the first – as deriving from it, through imitation. Similarly, the fourth appeared to echo the third, and this tripartite concept of repetition–imitation–derivation persisted in the pairs of identical notes that followed. And the imitative principle did not stop there. The very fact that the second note appeared to be generated by the first was itself emulated by the fourth being modelled on the third, and this pattern of ‘secondary’ replication also continued throughout the piece.
Some years later, I discovered that Edward Cone, although writing in relation to the syntax and rhetoric pertaining to more substantial components of music, had come to a similar view, and had formulated a succinct way of expressing it: “y is derived from x (y 
2. Zygonic theory – an introduction
Although it did not occur to me back in the 1980s, I later discovered that an effective way of explaining zygonic theory is through analogy with the construction of meaning in verbal language, utilising the thinking of the American-born writer and critic, Thomas Stearns Eliot. He proposed that the aesthetic response to literature combines three elements. These are the ‘objective correlative’ – a ‘set of objects, a situation, a chain of events which shall be the formula of that particular emotion’;[11] the ‘manner of representation’ (including, for example, the use of metaphor); and the sounding qualities and structure of the language itself (for instance, rhyme and assonance, syntax and form).[12] That is to say, meaning in a literary work arises from its semantic, syntactic and sonic elements working together ‘in an evocative fusion of content, structure and sound’.[13] This thinking may be represented as follows (see Figure 4).
Figure 4. Model of aesthetic response to language (after T.S. Eliot).
But ‘pure’ music has no external referents – no ‘objective correlatives’, to use Eliot’s term (Figure 5). So what is the source of musical meaning? Logically, it must stem from the fabric of music itself – from the sounds and the relationships between them that make up pieces.
Figure 5. Music has no ‘objective correlative’ or ‘manner of representation’.
It is my contention that each of these sonic elements potentially bears affect, causing or enabling an emotional response.[14] There appear to be two main sources of such responses: ‘expressive nonverbal vocalisations’ and ‘music-specific’ qualities of sound.
‘Expressive nonverbal vocalisations’ comprise the cues used to express emotions vocally in nonverbal communication and speech.[15] They are present cross-culturally,[16] suggesting a common phylogenetic[17] derivation from ‘nonverbal affect vocalizations’[18] and apparently embedded ontogenetically[19] in early maternal/infant vocal interaction.[20] It seems that these cues can be transferred in a general way to music, and music-psychological research over the last 70 years or so has shown that features such as register, tempo and dynamic level do relate with some consistency to particular emotional states.[21] For example, passages in a high register can feel exciting[22] or exhibit potency,[23] whereas series of low notes are more likely to promote solemnity or to be perceived as serious.[24] A fast tempo will tend to induce feelings of excitement,[25] in contrast to slow tempi that may connote tranquility[26] or even peace.[27] Loud dynamic levels are held to be exciting,[28] triumphant[29] or to represent gaiety,[30] while quiet sounds have been found to express fear, tenderness or grief.[31] Conversely, as Meyer asserts, “one cannot imagine sadness being portrayed by a fast forte tune played in a high register, or a playful child being depicted by a solemnity of trombones”.[32]
However, while these basic properties of sound appear to be necessary in determining musical expression,[33] they are not sufficient to evoke a response that is inherently musical. Indeed, any succession of sounds may induce a primitive emotional reaction according to the disposition of what Meyer[34] terms their ‘statistical parameters’ (which he takes to include register, dynamic level, speed and continuity). So what are the ingredients needed to arouse a specifically musical response?
One factor is the very nature of the sounds that are used in most styles and genres: They have intrinsically musical characteristics that, like those identified above pertaining to vocalisation, have the capacity to induce consistent emotional responses, within and sometimes between cultures. For example, in the West (and elsewhere), as Schönberg, Schenker and others discuss at some length, music typically utilises a framework of relative pitches with close connections to the harmonic series. Their idiosyncratic use, with context-dependent frequencies of occurrence and transition patterns, yields the sensation of ‘tonality’.[35] Such frameworks can accommodate different modalities, each potentially bearing distinct emotional connotations. In Indian music, for example, the concept of the ‘raga’ is based on the idea that particular patterns of notes are able to evoke heightened states of emotion,[36] while in the Western tradition of the last four centuries or so, the ‘major mode’ is typically associated with happiness and the ‘minor mode’ with sadness.[37]
While the reactions that individual or small groups of sounds can engender are important in setting the ‘auditory scene’ of music,[38] as they stand, they do not add up to a coherent musical response, merely amounting to a series of separate sensations pertaining to a sequence of discrete events. So how are these distinct, abstract responses bound together into a unified aesthetic experience – to create meaning that unfolds over time – during the course of listening to a piece of music?
Consider verbal language once more. Eliot’s ‘objective correlative’ is likely to be a series of events, actions, feelings or thoughts that are in some way reckoned to be logically related, each contingent upon one of the others or more through relationships of causation or other forms of dependency. These are represented through a linguistic narrative, which underpins readers’ or listeners’ coherent aesthetic response over time.
Figure 6. The linguistic narrative reflecting external events, ideas and feelings.
How does a comparable sense of coherence and unity come about in music, when it cannot borrow a sense of contingency from the external world? In the absence of an objective correlative, musical events can refer only to themselves.[39] Clearly, one sound does not cause another one to happen (it is performers who do that), but, as we saw above, one can imply another[40] through imitation, which yields a sense of derivation. That is, if one fragment or feature of music is created or heard in emulation of another, then the copy owes the nature of its existence to its model. And just as certain perceptual qualities of sound are felt to derive from one another, so too, I hypothesise, are the emotional responses to each. Hence over time a metaphorical (musical) narrative can be built up through abstract patterns of sound.
Figure 7. The musical narrative need make no external reference.
It is this hypothesis that forms the crux of zygonic theory. As noted in the first section of this article, the theory stemmed from musical ‘canons’, which are explicitly structured through one musical line consciously being made to copy another. Hence the first example of the theory in action will be taken from a passage of canonic writing: the opening of ‘Et in unum Dominum’ from the B Minor Mass. Here, Bach uses the derivation of the alto part from the soprano within a unified musical framework as a symbol of the Father begetting (not creating) the Son, which, according to Christian dogma (and Bach, by all accounts, was a devout believer), subsequently co-existed as parts of the same spiritual entity.
Figure 8. The opening of ‘Et in unum’ from Bach’s Mass in B minor (BWV 232); Symbolum Nicenum, No. 3.
Irrespective of the symbolism, it is easy to appreciate how each note in the alto voice, ensuing shortly after an identical event sung by the soprano, sounds irresistibly to the musical ear as though it derives from it. In the mind, each pair of notes appears to be connected via a mental ‘bridge’ that spans the two perceived sounds. Each of these may be termed a ‘zygonic relationship’ or ‘zygon’. In order to make analysis and understanding easier, it is sometimes helpful to represent these cognitive connections visually, and, at its simplest, this can be achieved through an arrow with a superimposed ‘Z’, as follows.
Figure 9. Zygonic relationships symbolising the sense of derivation of one note from another.
The solid-looking nature of these links should not be taken to mean that zygonic relationships have any material substance – they are hypothetical constructs: conceptual shorthand for a range of logically equivalent cognitive processes that we may reasonably suppose to occur during listeners’ engagement with music. For sure, the notion of a zygonic relationship can at best offer only a much-simplified version of certain cognitive events that may be stimulated by participation in musical activity. However, while simplification is necessary to make headway in theoretical terms, it is important to bear in mind that the single concept of a zygon bequeaths a substantial perceptual legacy, with many possible manifestations, not only potentially linking individual pitches, timbres, dynamics, durations and IOIs, but also prospectively existing between tonal regions, textures, processes and forms the same; over different periods of perceived time; and within the same and between different pieces, performances and hearings. Whatever their context, zygons, it is hypothesised, may function in a number of ways: reactively, in assessing the relationship between extant values, for example, or proactively, in ideating a value as an orderly continuation from one previously presented.
Given this variety, there is, of course, no suggestion that the one concept represents only a single aspect of cognitive processing. Hence, empirical evidence in support of the theory is likely to be drawn from a diversity of sources. Currently, for example, one can point to experiments in auditory processing[41] and work on expectation in a musical context, particularly that involving the perceptual restoration of omitted or obscured notes,[42] to support the presence of proactive zygonic-type processes. As we have seen, there is general support for the theory too in the wide range of music-theoretical and analytical sources in which the fundamental importance of repetition in music is acknowledged. These are itemised in Ockelford (1999). The zygons shown in Figure 9 are part of a large family of relationships whose members are catalogued exhaustively elsewhere.[43] Here, after a brief introduction to the nucleus of the family, other members will only be introduced as they are required to service the examples that follow.
Since zygons apply potentially to any features of musical sounds, it is sometimes necessary to identify which aspect a given relationship refers to, and superscripts can be placed after the ‘Z’ that is used in diagrams to make the position clear. For example, in Figure 10, ‘P’ refers to ‘Pitch’, ‘O’ to ‘Onset’ and ‘D’ to ‘Duration’. Figure 10 also depicts relationships that are not zygonic, through which no sense of implication is deemed to be felt, and which, therefore, merely conceptualise as a difference, ratio or other value that which is typically experienced as a qualitative connection between aspects of musical events.[44] They are symbolised with an ‘I’, which stands for ‘interperspective’ (that is, ‘between perceived aspects’ of sound) and, again, these may be qualified as required to avoid ambiguity through the use of superscripts.
Figure 10. Beethoven, Piano Sonata, Op. 110, 1st movement: examples of zygonic and interperspective relationships.
All such relationships, whether zygonic or not, can exist at different levels, according to their adjacency to the ‘surface’ of the music. Primary relationships (which bear the subscript ‘1’) are mental connections between the qualities of sounds themselves (for example, the interval between two pitches). Secondary relationships (subscript ‘2’) link primaries (acknowledging, for example, the difference between two melodic intervals). Tertiary relationships (subscript ‘3’) represent a considerable degree of abstraction from direct perceptual input, and are encountered relatively rarely, existing only in zygonic form; the part they play in the listening experience may not always be clear.[45] For example, in Figure 10, a tertiary zygon of onset reflects the fact that the IOIs between the opening notes of the first three bars decrease by a quaver in each case, and accords this regularity a structural status – at least in conceptual terms.[46] Empirical work would be required to determine whether this connection is usually, occasionally or rarely processed by listeners (albeit nonconsciously).
The imitation through which derivation is thought to occur may be exact (as, for example, in the case of the primary zygonic relationship of duration in Figure 10) or approximate (see, for instance, the secondary zygonic relationship of pitch between the descending intervals in bars 1 and 2). Observe that relationships (whether or not they are zygonic) that link different values use half-arrowheads (in contradistinction to full arrowheads that are indicative of identity). Note also that some arrowheads are open and some are filled – the former showing a link between single values, and the latter indicating a compound connection within or between ‘constants’ (typically, values extended in time) – implying a network of relationships the same. For fuller explanations, see Ockelford (1999; 2005a).
3. The Scope of the Theory
So much for the essence of zygonic theory. Since its inception some 25 years ago, which was stimulated by the curiosity of a young composer seeking to develop music-structural techniques that would be generally apprehensible to listeners, the theory has proved itself to be surprisingly versatile, being utilised in a range of musicological and interdisciplinary contexts – and it is this capacity to transcend methodological and epistemological boundaries that is, I believe, one of the key strengths of the approach.
First, zygonic theory has found a place in its own right as a way of explaining how musical structure ‘works’ – how it is created and cognised. This is set out in A Theory Concerning the Cognition of Order in Music,[47] The Cognition of Order in Music: A Metacognitive Study,[48] and Repetition in Music: Theoretical and Metatheoretical Perspectives.[49]
Second, the theory has found service as an analytical tool, for example, in relation to the first movement of Mozart’s Piano Sonata, K. 333,[50] Beethoven’s Piano Sonata, Op. 110,[51] Wagner’s ‘Die Alte Weise’ from Tristan und Isolde,[52] and Schönberg’s Klavierstuck, Op. 11, No. 1.[53]
Third, zygonic theory has proved useful as a metatheoretical and meta-analytical mechanism for interrogating other theoretical and analytical approaches, particularly Forte’s set theory as applied to music, and David Lewin’s transformational techniques.[54]
Fourth, the zygonic method has proved valuable in mapping the blended conceptual space that music and words together inhabit in song, for example, through an analysis of ‘Dido’s Lament’ from Purcell’s Dido and Aeneas.[55]
Fifth, the theory has found application in music-psychological contexts, in investigating constraints in music cognition,[56] similarity perception,[57] expectation in music,[58] creativity,[59] memory[60] and the perception of musical hierarchy.[61]
Sixth, it has been used to analyse musical influence and interaction in the context of improvisation.[62]
Seventh, it is being utilised to gauge how the structure and content of music are reflected in expressive performance.[63]
Eighth, the theory has been of value in modelling the musical development of children and young people with complex needs.[64]
Ninth, and finally, the zygonic approach has been used in epistemological discourse, to clarify the distinction between the modes of thinking of characteristic of music theory and music psychology.[65]
Future work is planned in these and other areas (see Section 7 below). In the sections that follow, three examples are chosen from the publications listed in the footnotes to show zygonic theory in action. These are analysis,[66] metatheory,[67] and interaction in improvisation.[68]
4. Using the Zygonic Approach as an Analytical Tool: An Exploration of the First Movement of Mozart’s Piano Sonata, K. 333
The following account of the first movement of K. 333 is adapted from Ockelford (1999; 2005a), and focuses largely on the opening bars. As we have seen, the zygonic approach points the analytical mind in a certain direction – seeking structural features of any type that are founded on imitation – and provides a conceptual and schematic framework within which findings of potential interest can be captured and interrogated. Working in this way, it quickly becomes apparent that, just like virtually all other music, K. 333 is replete with sameness and similarity in every domain and at all levels. Repetition is ubiquitous, and determining which of it is structurally significant – and the nature of that significance (in different listening contexts) – is, in my view, one of the principal challenges facing the analyst. The current reading is developed through comparisons with the Sonata Op. 5, No. 3 by J.C. Bach, both structurally and, consequentially, in terms of aesthetic response.
Like other pieces, K. 333[69] can be understood both as a unique artistic entity in its own right and as a member of corpora of works whose range and scale vary according to the degree of stylistic affinity used to define the group concerned. Hence K. 333 exists on one level as an example of the eighteen piano sonatas by Mozart, for instance, as well as figuring in the rather more substantial body of Classical sonatas, and contributing beyond that to the Western tonal repertoire as a whole. This distinction is articulated by Meyer[70] in terms of critical analysis, which “seeks to understand and explain what is idiosyncratic about a particular composition” and style analysis, which is “concerned with discovering and describing those attributes of a composition which are common to a group of works … similar in style, form or genre.” Of relevance in the current context is the fact that the simultaneous presence of individuality and commonality within K. 333 (as within any work) implies that there are essentially two types of structure operating together: organisation that features in a number of pieces, forming a more or less consistent ‘background’, against which other patterning of a novel nature occurs, specific to the sonata.[71] We begin with an overview of the former, before considering how the latter is, as it were, superimposed upon it.
It is in the domains of pitch and perceived time that the great majority of ‘background’ organisation occurs (and which is by far the most musically significant and sophisticated). For example, underlying the perceived temporal structure is the presence of an essentially regular beat, which is maintained throughout the movement (subject, for sure, to interpretive variation in performance). This suggests that zygonic activity in the domain of perceived time played a part in the creation of K. 333 (and has subsequently been stimulated in listeners’ minds), both within the first movement itself and between this and other movements. Moreover, although Mozart left no specific indication of tempo, the first movement of K. 333 is typically executed at a rate similar to those adopted for many others: further evidence of primary zygonic imitation in terms of both composition and performance.[72] The choice of metre (common time) and its constancy may be considered to have been derived interoperatively[73] too. Then, IOIs between successive notes fall within a limited range, which is commonplace in other pieces, implying intraopus and interoperative imitation.[74] The IOIs correspond closely to the set of durations that Mozart deploys, a consequence of the fact that most notes succeed one another contiguously. Only eight different durations are utilised in over 2,500 discrete events, suggesting the operation of extensive systems of zygonic relationships.[75] The fact that similar durational sets are found in stylistically congeneric movements also indicates the presence of interoperative organisation.[76] Stylistically, the distribution of relative durational values also tends to be highly structured, with just two note-lengths (in the ratio 2:1) typically accounting for over 80% of all those used in Western classical pieces, according to Paul Fraisse.[77] This finding is supported by the analysis shown in Figure 11, which indicates, moreover, an overall 86% similarity in the distribution of relative durations pertaining to the first movements of three broadly representative piano sonatas by Mozart (K. 284, K. 310, K. 311) in addition to K. 333.[78]
Figure 11. Imitation of the distribution of relative durational values in the first movements of four Mozart piano sonatas.
Similarly, the distribution of secondary inter-onset ratios (between adjacent IOIs linking successive notes) is tightly controlled. A given interonset ratio is, by a considerable margin, most likely to be followed by another the same (this occurs in just over 78% of cases).[79] The ratios 1 : 2 and 2 : 1 appear with the next greatest frequency (6% each). Only two other ratios are used in more than 1% of cases – 3 : 1 and 1 : 4. Hence, structuring on a substantial scale is implied at the tertiary zygonic level. Since the distribution is typical of other stylistically congeneric movements, the presence of interoperative zygonic organisation is indicated as well. See Figure 12, where the 92% similarity is calculated as shown in Footnote 78.
Figure 12. Patterns of imitation of secondary interonset ratios within the first movement of K. 333.
Elsewhere,[80] I discuss the relevance for listeners of statistics such as these (and those pertaining to pitch that follow), and examine how zygonic organisation underpins expectation in the process of hearing and re-hearing the music. How it is that such distributions come to be used time and again by composers, with the large-scale imitation at a probabilistic level that these imply, is an intriguing question that awaits future research.
The intervals between adjacent notes in the melody reveal substantial organisation across the movement as a whole. A little over 90% of the intervals used are a perfect 4th or smaller, and of the 43 different categories that appear, 10 occur on more than 2% of occasions (Perfect unison, minor 2nd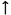
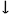
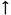
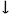
Figure 13. Imitation of the distribution of successive melodic intervals between the first movements of representative piano sonatas by Mozart.
Harmonically, the first movement of K. 333 is highly organised. The underlying harmonies, discounting the ornamental effects created through the interaction of vertical sonorities with the horizontal movement of melodic lines, are entirely tertian in construction (built up from major and minor thirds), a feature common to many other pieces.[86] We can surmise, therefore, that intraopus and interoperative imitation are present on a large scale. Even given these tight constraints, Mozart chose to restrict his harmonic palette further: the first movement of K. 333 is dominated by major and minor triads and 7th chords and their inversions, suggesting that primary zygonic constant systems of harmony function as shown in Figure 14.[87] These areas of imitation also extend interoperatively.
Figure 14. Primary zygonic constant systems of harmony associated with the first movement of K. 333.
The tight statistical structure to which harmonic function conforms can be illustrated in several ways. For example, harmonies constructed on the tonic and dominant[88] account for 68% of the total, while chords built on one of four scale degrees (tonic, supertonic, subdominant and dominant) appear 90% of the time. The fact that this distribution is similar to that displayed in other pieces indicates the presence of interoperative imitation (see Figure 15). The transitions between successive harmonies are also subject to close imitative control, both in intraopus terms and interoperatively. For example, transitions of +4 degrees or +5 degrees account for between 63% and 81% of all primary interperspective values. The relative durations of tonal regions show marked interoperative similarities too.
Figure 15. Imitation of the distribution of harmonic degree in the first movements of piano sonatas by Mozart.
These, then, are some examples of the ‘background’ organisation to which the first movement of K. 333 is subject. There are a number of other similar forms of structure which could equally well have been chosen by way of illustration[89] such as the orderly disposition of the ‘relative metrical location’ (‘RML’)[90] of notes, and, in the domain of pitch, the use of an intervallic framework corresponding to the diatonic major scale (often extended through chromatic auxiliaries), whose members are felt to discharge discrete tonal functions. Then, there are more general structural principles to which K. 333 conforms, including its essentially two-part texture – typical of piano music of this genre – in which the RH and LH parts respectively fulfil the roles of melody and accompaniment, the latter offering harmonic and rhythmic support to the former, which has greater immediate perceptual salience, and is typically the chief determinant of musical identity. Similarly, in terms of form, taken to be the interaction of themes and tonal regions at the highest structural level,[91] the first movement of K. 333 respects the conventions of the Classical sonata.
Taking all these factors into account,[92] zygonic theory suggests that, at any given point in the music, over 30 different forms of ‘background’ organisation – incurred through interoperative imitation – are potentially in play. From a cognitive-psychological point of view, what role the interperspective relationships implied by this account actually fulfil in the listening process, and how the brain is able to handle so much simultaneous information (if indeed it does), are matters for future empirical work to determine. As far as music theory is concerned, the main issue would seem to be how Mozart (or any other composer) could possibly devise pieces of any originality when working within such tight stylistic constraints. However, the structure-bearing capacity of traditional musical materials is immense, giving composers effectively limitless scope for creating new abstract patterns in sound. For example, the first three or four notes of a tune are all that is typically required to identify it as unique, and even having regard only to the domain of relative pitch-class, six or seven values will usually suffice, as Harold Barlow and Sam Morgenstern’s thematic catalogue of over 10,000 themes from the Western classical instrumental repertoire (1948) shows.
We now investigate how the features that give K. 333 its unique identity function within the framework of ‘background’ structural forces that have been identified. Since space is limited, we will make particular reference to the opening four bars. To set this analysis in context, K. 333 will be considered in relation to J.C. Bach’s Piano Sonata Op. 5, No. 3, one of a set with which Mozart is known to have been acquainted[93] and to which a number of characteristics appear to be attributable.[94] From the outset, there is a close resemblance between the melodies: the patterns of relative pitch (‘profiles’) are similar, and the melodic cell of four notes that opens K. 333 is very much the same as a cell embedded in Op. 5, No. 3. In Figure 16, this potential route of derivation is shown through a ‘syzygy’ (depicted as a ‘z’ within an ‘s’) – a particular type of zygonic relationship involving profile (the pattern of intervals) and rhythm considered together, which acknowledges the unique perceptual and conceptual importance of this combination in musical terms. The use of appoggiaturas evident in these excerpts continues to be an important feature of both melodies as they unfold, suggesting zygonic interoperative connections. The Alberti-style left hand parts are very similar too, indicating further syzygial links. In considering the first four bars of each movement as a whole, the affinities between phrase structure and ‘harmonic rhythmic pattern’[95] strongly suggest interoperative imitation at this higher level in the structure (see Figure 17).
Figure 16. Potential derivation of the opening melodic cell of K. 333 from J.C. Bach’s Sonata, Op. 5, No. 3.
Figure 17. Zygonic relationships of ‘harmonic rhythmic pattern’ and phrase structure presumed to link K. 333 and Op. 5, No. 3.
On the face of it, then, the two openings are very similar, and to listeners familiar with the Classical style, they both make musical sense: they are coherent and complete. Yet K. 333 and Op. 5, No. 3 are not the same, and, arguably, do not constitute equally fine works of art. To this listener at least, K. 333 offers a more fulfilling aesthetic experience – a judgement that others have made over time, for the Mozart sonata has long featured in the standard piano repertoire, while the Bach is seldom heard.[96] Why should this be? Convincing explanations of how it is that one piece should intuitively be felt to have greater musical worth than another that is similar have proved elusive (if not contentious). Réti, for example, argued that aesthetic value is linked to the notion of unity, which in turn depends on the variation of ‘one identical musical thought’, both within and between movements.[97] However, both K. 333 and Op. 5, No. 3 are replete with internal similarity, and (as we have seen) each evolves organically from an initial scalar descent. Meyer, too, has problems with Réti’s theory, and proposes, rather, that it is the “inhibition of goal-oriented tendencies” that accounts for value in music:[98] That is, “if the most probable goal is reached in the most immediate and direct way, given the stylistic context, the musical event taken in itself will be of little value”.[99] There are a number of ways in which such inhibitions can be induced, including, for example, through the use of appoggiaturas, whereby the arrival at a consonant melodic tone (which is implied by what has gone before) is delayed through the interpolation of an accented dissonance. According to Meyer, the momentary doubt that this delay sows in the mind of listeners both triggers and is subsequently expunged by the feeling of pleasure engendered by the expected note once it finally arrives, and it is this circuitous route to fulfilment that creates affect.[100] Indeed, in Meyer’s view, uncertainty is a key element in the aesthetic process.[101] Elsewhere, I have argued that this thesis may be untenable,[102] not least because the enjoyment of pieces generally increases with familiarity,[103] and, introspection suggests, it is the very anticipation of resolution that enables us to make sense of the transitory dissonance as it occurs.[104] The merits of this argument notwithstanding, the use of appoggiaturas, at least in a quantitative sense, cannot in any case account for the perceived difference of aesthetic worth between Op. 5, No. 3 and K. 333, since both utilise nine such events in the first four bars, implying a similar level of ‘inhibition of goal-oriented tendencies’ in each. The manner in which the appoggiaturas are used differs subtly from one piece to the other, however, and it is through analysing this difference in terms of ‘content’ (the intrinsic nature of the musical materials that are used) and ‘structure’ (the organisation of those materials through zygonic relationships) that light will be shed on the more general issue of the relative value of the compositions in aesthetic terms.
In both excerpts, appoggiaturas provide important affective triggers, set off by the sense of movement from tension to resolution that each evokes. In Op. 5, No. 3, this effect is felt most powerfully in bars 2 and 4 where the discords that are created extend for two complete beats. However, while these and the other appoggiaturas – key aspects of the music’s expressive ‘content’ – are integrated into the structure of the passage, the connection between the two is not rigorously worked through. So, for example, though the initial figure includes two appoggiaturas, enriching the simple scalar descent, these are lost in the subsequent ascending scale (despite this being derived from the opening through imitation), although a further appoggiatura appears incidentally at its climax (at the end of bar 1). And while the two-beat appoggiatura in bar 2, the first main expressive gesture of the piece, is conceivably, though at most weakly, zygonically linked to the three that precede, there is no real sense that it grows organically from them. Bars 3 and 4 proceed along similar lines, whereby despite their intervallic pattern in structural terms deriving from bars 1 and 2, the asymmetrical nature of the transposition means that the appoggiaturas – key features of expressive content – do not read across.
Figure 18. Irregular relationship between appoggiaturas and pitch structure in the opening of J.C. Bach’s Sonata, Op. 5, No. 3.
In K. 333, however, the position is different. Structure and content are systematically yet unobtrusively integrated, such that the logic of the music and its expressive character – the carrier and its message – are fused in an abstract discourse that is wholly persuasive. Listeners are propelled straight into the action by the initial descending figure, comprising two appoggiaturas which lead the ear naturally to a third that is augmented and unambiguously establishes the tonic on the downbeat of the first complete bar. However, this proves to be just a stepping stone to a fourth appoggiatura, which, augmented again, bears even greater expressive emphasis. Significantly, this falls on the supertonic minor, hinting at emotional depths lying beneath the surface elegance of the music that find fuller expression later, particularly in the development section. What makes the appoggiatura – in its own right an expressive gesture – all the more telling, is that both structure and content (4–3 in a minor context) are locked in to what has gone before, deriving from the preceding material in a number of ways. As well as growing from previous appoggiaturas through transposition and rhythmic augmentation, the F and 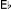
Figure 19. Derivation of the fourth appoggiatura in K. 333 from preceding material.
In terms of content, this fourth appoggiatura, heard structurally as a product of the first three, does more than replace in current consciousness their affective qualities: it transforms them. Through approximate zygonic imitation the major harmonic context of the earlier appoggiaturas becomes minor,[107],[108] which, given the prevailing 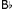
Figure 20. Systematic use of appoggiaturas in the opening four bars of K. 333.
There are other ways, too, in which structure and content are felicitously worked together. The opening narrative design is one in which a brief ‘statement’ (the first seven notes) is followed by a ‘response’ (the next five), followed by a further similar arrangement. Each statement-response pair forms a unit of more substantial proportions at the next level in the structural hierarchy, the first of which itself functions in its own right as a statement and the second a response. To achieve this narrative effect in music requires that one abstract gesture follow logically from another, yet differ from it. This is accomplished in different ways at different levels in the hierarchy. At the higher level, the response is a transposed version of the statement with slight modifications. At the lower level, statement and response are linked through retrogression in the domain of pitch, forming subtle connections that throw other zygonic relationships (such as those linking the appoggiaturas) into relief.[109]
Figure 21. Effect of statement and response at different levels in the structural hierarchy accomplished through complementary forms of zygonic structuring.
Lastly, we consider the way in which melody and accompaniment are integrated in terms of structure and content. In Op. 5, No. 3, an opening connection is made through retrogression, but the largely simultaneous ascent and descent of the two parts has a neutralising effect, and the music has a somewhat ‘four-square’ feel about it. Following this opening relationship, there are no further motivic links of significance, and the Alberti bass fails to rise above the mundane, merely supplying the melody with a succession of rhythmised harmonies. In contrast, in K. 333, while retrogression is also used initially to tie in the left hand part with the right, since the accompaniment follows the lead of the melody, the imitation delivers a sense of forward movement, which is maintained as the overlapping of motivic units between treble and bass continues. The effect is emphasised, moreover, by the off-beat start to the figuration, which puts a spring in the step of the music, and, subsequently, through repetition of the opening quaver rest, allows it to ‘breathe’. In the second half of the first bar, model and imitation are reversed, as the right hand imperfectly echoes the left, whereby the 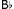
Figure 22. Limited integration of melody and accompaniment in Op. 5, No. 3 and motivic integration of melody and accompaniment in the opening of K. 333.
Finally, note that other subtle details of design exist on a formal level, too. For example, the bipartite structure of the melody (as shown in Figure 21), in which the second half is generated from the first through transposition, complements the sense of return engendered by the accompaniment, in which the opening harmony and figuration are repeated (with slight variation) at the end of the four bars. These two forms of symmetry interact to produce the poise so typical of the Classical style.
Figure 23. Complementary organisation of melody and accompaniment in the opening of K. 333.
The integration of structure and content that characterises the opening of K. 333 continues as the movement unfolds, not only within sections, but between them as well. For example, the opening of the second thematic group (from bar 23) is closely related to the first, both in its descent from the sixth degree of the scale, and also in its identical use of appoggiaturas.
Figure 24. Integration of structure and content across first and second thematic groups in the first movement of K. 333.
Then, the range of the opening melody (from leading note up to submediant) is respected on a number of subsequent occasions, for example, from bar 15. In bar 43, the interval explicitly becomes part of proceedings, forming the climax of the passage that begins at bar 39. Hence, once more, the expressive content of the music is held together through zygonic relationships functioning in addition to those demanded by the structure of the Classical sonata, imbuing the music with a sense of aesthetic unity that formal connections alone could not guarantee.
Figure 25. Use of melodic range as a unifying feature in the first movement of K. 333.
What does this zygonic approach to K. 333 tell us? First, that before Mozart even started work on the sonata, he was destined to operate within a tight framework of ‘background’ organisation, determined in part by extramusical factors, such as the limitations on the human capacity for perceiving and processing sound, and the physical constraints posed by the fortepiaNo. More significant, though, were intramusical considerations – in particular the composer’s (doubtless nonconscious) decision to work within the parameters that defined the style of Classical keyboard music in late eighteenth century Vienna. As a result, the sonata is replete with many forms of organisation that are variously common to some, many or virtually all other pieces. Yet, the capacity for potential combinations of perspective values to exist is such that this degree of control is probably necessary for listeners to be able to make sense of music – particularly on a first hearing; and it was, after all, essential for Mozart’s survival as a composer that his new compositions were instantly accessible. His genius lay in the ability to craft something original and of lasting value within such tight constraints, when most music composed failed to satisfy either criterion. How did Mozart do it? Zygonic analysis suggests that the aesthetic worth of K. 333 is ultimately attributable to the consummate fusion of structure and content. Of course, it is not possible, on the basis of this one brief account, to produce a theory that would enable us to predict the prospective aesthetic value of a piece on the basis of certain patterns of zygonic relationships linking particular perspective or interperspective values. But zygonic theory gives us a tool with which at least a partial interrogation of this thorny issue may be possible, and it is conceivable that general principles will emerge once a number of other comparable analyses have been undertaken. It is clear, however, on the basis of the evidence presented here, that the mere presence of conformance – whether to the deep tonal forms unearthed by Schenker, or of the motivic type identified by Réti – does not in itself ensure musical worth. Nor, as Meyer would have it, does it appear that a composer’s capacity for thwarting, manipulating and eventually realising the expectations that are aroused in listeners by sophisticated musical patterning is sufficient. Rather, it is my contention that what makes music effective – even great – is the manner in which its inherent (or learnt) expressive qualities, its ‘content’, are integrated with structure, through zygonic relationships.
5. Deploying the Zygonic Approach Metatheoretically: Exploring Issues in Set Theory
In this section, we consider how zygonic theory can be deployed metatheoretically – to interrogate the principles and procedures of set theory – using material taken from Ockelford (2005a).
In brief, the application of set theory to music was intended to offer a mechanism through which the structure of the atonal music of Schoenberg, Webern and Berg and other composers written at the beginning of the twentieth century could be explained systematically.[110] However, as Jonathan Dunsby notes,[111] its remit subsequently widened considerably, to embrace the works of composers such as Skryabin and Liszt; and, with the development of pcset genera theory, whose species’ names notably include ‘dia-tonal’, its range of applicability broadened still further.[112]
The basic principles and procedures of set theory were conceived in relation to pitch, and guided by the assumption that all values and the relationships between them (unlike those in tonal music) are, by default, equal in structural terms. Hence the immediate analytical challenge that they pose is one of scale – how to reduce the available data to manageable proportions – since even as short a piece as the sixth of Schoenberg’s Six Short Piano Pieces, Op. 19, comprising only 52 notes, is linked internally through 1,326 primary and 878,475 secondary latent relationships of pitch. An initial process of reduction was devised that borrowed a number of concepts from Schoenberg’s ‘serial’ compositional procedures. This holds that one set of pitches can be regarded as equivalent to another, irrespective of transposition or inversion, the octave in which values are realised, whether or not they are repeated, and, additionally, the order in which they occur. The mental processing underlying this form of equivalence may be illustrated as follows (see Figure 26).[113] The relationships between the ‘ordered pitch-class sets’ (which reflect actual values of pitch) and the ‘pcsets: prime form’ (which are wholly abstract representations – effectively intervallic frameworks) are particularly worthy of note,[114] linked, in terms of the present theory, through ‘profile’ (relative values of pitch).
Figure 26. Zygonic processes through which pcset equivalence is gauged (analysis adapted from Meyer and Shreffler 1993).
Note that the descriptor of these identical ‘pitch-class sets’ (‘pcsets’) in prime form (‘x-y’) follows that developed by Forte (1973). To what extent abstractions of this type, which, as the zygonic analysis shows, demand a high level of intellectual and auditory processing, have any phenomenological reality – and therefore relevance to listeners – has been the subject of some debate and a limited amount of empirical research.[115] This has served to highlight certain conceptual and methodological differences between the sister disciplines of music theory and music psychology,[116] and the metatheoretical zygonic approach adopted here points up some of the perceptual and cognitive challenges that pitch-class set theory presents. One issue is that, while reduction of the musical ‘surface’ to pcsets diminishes the amount and variety of information to be processed, the potential number of orderly relationships within many sets, particularly the larger ones, is very great nevertheless. That is to say, even if pcsets are in some way paralleled in cognition, then the task they present the musical mind, striving to make sense of the sounds that assail it, is still formidable, as, in the ongoing search for commonalities, a continual succession of pitch-classes and interval-classes are compared one with another. But which of these relationships are likely to be significant and which are not? The principal clues that would have helped, particularly the order in which events occur, and their relative emphasis through metrical placement, duration, register, timbre or attack are irrelevant once pcsets have been formulated through the initial process of segmentation.
Take, for example, set 4-25; prime form {0,2,6,8}. One realisation, taken from Forte[117] is as follows – see Figure 27. The six primary interperspective relationships that potentially link the four values of pitch are described in Forte’s vector [020202] for 4-25, which lists the number of interval-classes in ascending order, starting with ic1 (a difference of a semitone). Since repeated values never occur in Forte’s pitch-class sets, ic0 and, therefore, primary zygonic relationships, are not a possibility.
Figure 27. One realisation of the pcset 4-25 and its internal network of primary interperspective relationships (after the analysis of Forte 1973, 86ff).
However, with secondary relationships, the position is altogether different. Three potentially zygonic secondary relationships and twelve others prospectively link the primary interval-classes (or ‘ic1’s) as follows.
Figure 28. The network of secondary interperspective relationships pertaining to 4-25 (where ‘Rel-pc’ captures the abstract notion of pitch-class in a pcset: prime form).
These data can be captured in what may be termed a vector of ‘secondary interval-classes’ (‘ic2’s) for 4-25, written thus:[118]
[3. 0 8 0 4 0 0]2
The category ic20 heads the list and, for clarity, is separated by the succeeding values with a dot.[119] Ic2 vectors can be derived by calculation. Given the vector [a.bcdefg]1, then the number of:
ic2 0 | = | ½ a (a – 1) + ½ b (b – 1) + ½ c (c – 1) + ½ d (d – 1) + ½ e (e – 1) + ½ f (f – 1) + ½ g (g – 1) |
ic2 1 | = | (a • b) + (b • c) + (c • d) + (d • e) + (e • f) + (f • g) |
ic2 2 | = | (a • c) + (b • d) + (c • e) + (d • f) + (e • g) |
ic2 3 | = | (a • d) + (b • e) + (c • f) + (d • g) |
ic2 4 | = | (a • e) + (b • f) + (c • g) |
ic2 5 | = | (a • f) + (b • g) |
ic2 6 | = | (a • g) |
For example:
3-6 | {0, 2, 4} | ic1 vector [0. 0 2 0 1 0 0]1 | ic2 vector [1.0 2 0 0 0 0]2 |
4-23 | {0, 2, 5, 7} | ic1 vector [0. 0 2 1 0 3 0]1 | ic2 vector [4.2 3 6 0 0 0]2 |
5-1 | {0, 1, 2, 3, 4} | ic1 vector [0. 4 3 2 1 0 0]1 | ic2 vector [10.20 11 4 0 0 0]2 |
6-Z28 | {0, 1, 3, 5, 6, 9} | ic1 vector [0. 2 2 4 3 3 2]1 | ic2 vector [15.39 32 20 10 4 0]2 |
7-35 | {0, 1, 3, 5, 6, 8, 10} | ic1 vector [0. 2 5 4 3 6 1]1 | ic2 vector [35.66 50 40 17 2 0]2 |
8-19 | {0, 1, 2, 4, 5, 6, 8, 9} | ic1 vector [0. 5 4 5 7 5 2]1 | ic2 vector [58.120 92 65 33 10 0]2 |
9-11 | {0, 1, 2, 3, 5, 6, 7, 9, 10} | ic1 vector [0. 6 6 7 7 7 3]1 | ic2 vector [96.197 154 105 60 18 0]2 |
As one would expect, there is, generally speaking, a growth in the number of relationships as the cardinality of pcsets increases – a trait that is particularly marked in the case of secondary relationships – and it seems reasonable to assume that this corresponds to a decreasing tendency of sets to be fully perceptible in structural terms as they grow in size and, therefore, complexity. This likely perceptual trend is compounded by the fact that the internal orderliness of pcsets (or ‘zygonicity’ in terms of the present conceptual framework) by and large falls as their cardinality rises. ‘Zygonicity’ is an expression of the proportion of the potentially zygonic relationships between identical values of a given rank to the total number present, that is:
a / (a + b + c + d + e + f + g) x
Hence the zygonicity at secondary level (‘zyg2’) of the sets listed above (to three decimal places) is as follows:[120]
zyg2 (3-6) | = | 0.333 |
zyg2 (4-23) | = | 0.267 |
zyg2 (5-1) | = | 0.222 |
zyg2 (6-Z28) | = | 0.167 |
zyg2 (7-35) | = | 0.153 |
zyg2 (8-19) | = | 0.152 |
zyg2 (9-11) | = | 0.152 |
The cognitive relevance of these figures, even in approximate terms, is not clear. In any case, whether from a perceptual or conceptual standpoint, it is helpful to put them in a wider context – to move beyond Forte’s list of pcsets, and regard repeated elements as distinct. Self-evidently, maximal zygonicity occurs with series of notes of the same pitch. For example:
Figure 29. A set of pitch-classes the same has maximal zygonicity.
Here, the ic vectors [6. 0 0 0 0 0 0]1 and [15. 0 0 0 0 0 0]2 are indicative of a zygonicity of 1 at both primary (zyg1) and secondary (zyg2) level.[121] A further useful reference point is the secondary zygonicity of the twelve-note set (and, therefore, of any twelve-tone row), whose ic vectors are [0.12 12 12 12 12 6]1 and [345.648 504 360 216 72 0]2. Hence, zyg1 = 0.161.[122]
A crucial preliminary stage in set-theoretical analysis is ‘segmentation’ – “the procedure of determining which musical units in a composition are to be regarded as analytical objects”.[123] Notwithstanding Forte’s subsequent reservations about his attempts in The Structure of Atonal Music to provide guidelines for the analytical operation of segmentation,[124] and despite the fact that, twenty-five years later, different analysts can legitimately adopt different approaches to segmentation to achieve different results,[125] the original underlying principles have retained their relevance. Forte defines primary segments as those that can be isolated as units “by conventional means, such as a rhythmically distinct melodic figure. For the most part such segments are indicated by some notational feature, for example, a rest or beamed group, and offer no novel problems. Similarly, chords, in the sense of vertical groupings, and ostinato patterns are not difficult to identify as primary segments”.[126] To the extent that ‘notational features’ reflect groups formed through auditory perception, the zygonic ordering underlying Gestalt mechanisms can be invoked to explain how primary segmentation can reasonably be achieved.[127]
However, according to Forte, such techniques do not necessarily “adequately reveal structural components”,[128] since atonal music is structured at levels beneath the immediate surface. Hence methods of segmentation may be ‘concealed’. In order to uncover the hidden organisation of pitch, Forte recommends the procedure of ‘imbrication’: “the systematic (sequential) extraction of subcomponents of some configuration” – that is, listing all the pcsets contained within a passage in the hope that this will reveal relationships that were not otherwise apparent.[129] While it is conceivable that such a process may uncover pitch structures of musical interest that listening alone would fail to detect, there are a number of problems with this technique. For example, pcsets may not have been apparent in the first instance because they could not be extracted perceptually from large and complex aggregations of notes (and, how, therefore, could they be of structural relevance to listeners?). Moreover, if it is appropriate to adopt mechanistic, rather than perceptual, approaches to the discovery of structure, then, logically, these should be rigorous and comprehensive to ensure that items of potential relevance are not missed. However, the sheer scale of potential organisation that a process such as imbrication – systematically applied – throws up is staggering, and the mass of data is correspondingly difficult to manage.[130]
We shall consider this issue in the context of the first of Schoenberg’s Three Piano Pieces, Op. 11, taking as a starting point Forte’s (1981) analysis, entitled The Magical Kaleidoscope. The opening 4½ bars are segmented thus (see Figure 30), with 14 different pcsets (in prime form) occurring with the frequencies set out in Figure 31.
Figure 30. Pcsets identified by Forte (1981, 139–40) in the opening of the first of Schoenberg’s Three Piano Pieces, Op. 11.
Figure 31. Frequency of occurrence of pcsets in the opening of Forte’s (1981) analysis.
Clearly, to understand this analysis – to hear Op. 11, No. 1 as Forte hears it – it is crucial to appreciate the reasons that lie behind this segmentation. Some pcsets derive self-evidently from the division between theme and accompaniment – for example, 6-Z10 and 6-Z16 in (a). The selection of other sets, however, such as 6-21 in (b), is less immediately apparent – being chosen since they constitute ‘structural components’ which ‘subsequently become important’.[131] The unspoken constraint that Forte appears to apply in arriving at these structural segmentations is that the pitches concerned should be partly or wholly simultaneous, or contiguous, with at least one other (although the final ‘B’ in (c) extends this rule). Evidently, these sets need not respect textural divisions, since sometimes they embrace components of the theme and the accompaniment.
So much for the principles underlying the derivation of segments. Their status is less clear, however. There is no direct evidence, either in the manuscript or in verbal commentaries, that Schoenberg conceived the opening of the piece in terms of the 28 pcsets Forte identifies, or, indeed, that sets of any description were used as a tool to facilitate its composition (in contrast to the way that tone rows were subsequently described and used). Could it be, then, that pcsets nevertheless offer a valid model of how listeners intuitively make sense of the work’s structure? Again, there is no empirical evidence of this – quite the contrary. While the process of formulating even a single pcset from the relevant material presented in abstraction demands a high level of aural and intellectual skill (as the model in Figure 25 shows, with three distinct processes to be worked through for each note), to identify sets in the context of a living piece of music is an almost inconceivably difficult task. Whether we assume that sets are imagined prospectively, acknowledged retrospectively or perceived as a combination of the two, it is not clear how one is to know which of the 208 options to listen out for. Presumably, different possibilities have to be tried, with many being rejected en route to the final ‘reading’. Then, consider the specific challenges posed in the opening 4½ bars of Op. 11, No. 1. An initial difficulty is that theoretically discrete pitches may be merged into single chordal percepts. A further, fundamental, issue is that, according to Forte’s analysis, 28 sets occur in around 12 seconds, which, given the data in Figure 30, means that, for his analysis to be appreciated in full, 133 allocations of values to sets have to be made, at a rate of something over 10 a second.[132] Since there are only 23 distinct pitches in the passage in question, this implies a high degree of multifunctionalism – with each note appearing in an average of around six sets, and some, for example, the D in the tenor part of bar 4, finding a place in 12.
Perhaps, then, the structural revelations viewed in The Magical Kaleidoscope are significant neither to understanding the process of composition nor to how listeners apprehend the piece, but encapsulate interesting and intellectually valid observations in their own right. In which case, the issue to consider is whether Forte’s insights, judged by the analytical parameters he sets himself (explicitly or by implication), reflect an accurate and balanced picture of events, or possibly present the most notable abstract structural features. A cursory examination of the musical text suggests not. Take, for instance, the trichord 3-3. Forte deems three appearances as being worthy of note. However, there are a large number of others which appear to be at least as structurally relevant as those Forte highlights, together involving all available pitches. They include:
Figure 32. Further examples of the pcset 3-3 in the opening of Schoenberg’s Op. 11, No. 1.
This suggests that it would be appropriate to attempt a full process of analytical imbrication, to determine just which pcsets potentially exist in the passage, and in what numbers, since this complete set of data should provide the context in which to appraise Forte’s choices of segmentation, and may additionally bring to light other features of structural interest. In order to do this systematically, we will remodel the passage as a table of possible transitions in the domain of pitch. Using the principles adopted by Forte of permitting only those transitions between notes that are contiguous or simultaneous (in part or in whole) yields the following 79 possibilities (the dotted lines indicate necessary precursors to certain transitions.)
Figure 33. Possible transitions between partly or wholly simultaneous and contiguous notes in the opening four-and-a-half bars of Schoenberg’s Op. 11, No. 1.
Using this model, it becomes evident that every pcset of the 208 prime forms that are available is represented! How, then, is one to determine which are of greater structural significance than others? Perhaps by their frequency of occurrence. The figures for sets of lower cardinalities are as follows (observe that, for the purposes of compiling these data, Forte’s principle of ignoring repeated values is followed.)
Figure 34. Distribution of pcsets of cardinality 3, 4 and 5 in the opening four-and-a-half bars of Schoenberg’s Op. 11, No. 1.
Immediately, one is struck by the overwhelming number of sets that can be derived from a series of only 22 notes.[133] The tables show that the number of appearances of pcsets of a given size rises by a factor of approximately x3.5 as cardinality is increased by +1, a trend substantiated by initial research into hexachords, which suggests that they number something over 10,000 in this short passage alone. These numbers are so large that they can only be of statistical interest, though even their relative distribution indicates nothing of structural significance.[134]
What, though, of the relationships between them? Again, the predominant characteristic is the sheer scale of things, with, for example, sets of cardinality 3 prospectively linked through 34,191 primary relationships, of which 3,227 are potentially zygonic (9.44%); sets of cardinality 4 potentially bearing 390,286 primary relationships, of which 16,073 may be zygonic (4.12%); and sets of cardinality 5 potentially connected through 4,965,976 primary relationships, of which 171,309 may be zygonic (3.45%). Note that these figures, large as they are, do not include the numerous other relationships that potentially exist between sets and their complements. Even without these additions, there would appear to be little if any musical significance in the data. Clearly, with so much potential orderliness pertaining to pcsets, the indiscriminate analyst could highlight any form of patterning that he or she chose from the myriad of relationships that are present. However, the great majority of any apparently structural characteristics so identified would not pertain specifically to Op. 11, No. 1, but would exist merely as a consequence of deriving collections of pitch-classes from a highly constrained universal set.
In summary, then, Op. 11, No. 1 may or may not be a ‘magical kaleidoscope’: it is impossible to say through analysis based on the systematic extraction of pcsets. This is because the criteria for deriving structurally significant relationships from the millions that are available are not inherent in the data that segmentation through imbrication itself generates. Rather, to determine which sets and relationships are likely to be important, one has to rely on other features present in the domain of pitch or in other perspective domains that were stripped away in the initial process of extracting the pcsets – and inevitably, such complex, multidimensional decisions must rely largely on the musical intuitions of the analyst. However, this runs counter to the reason for adopting a systematic approach in the first place, which was to uncover potentially ‘hidden’ organisation of pitch; it also renders the procedure of imbrication redundant.
So it would seem that, if the process of pcset analysis is to deliver truly musical insights, then perceptibility must figure in the procedure of segmentation that is adopted. Experience suggests that, other things being equal, perceptibility will tend to be enhanced when the pcsets are relatively short; when the pitches from which they derive are readily heard in the texture; when sets regarded as equivalent are derived with relatively little or with similar manipulation of their source material; and when orderly relationships between pcsets run in parallel with other zygonic connections. These issues, and the manner in which set-theoretical analysis interfaces – and can be integrated – with other approaches through the utilisation of a common zygonic metatheoretical framework, underlie the exploration of the opening bars of Op. 11, No. 1 to be found in Ockelford 2005a.[135]
We have taken the presence of potentially zygonic relationships between pcsets as one indication of structural orderliness. However, these relationships form only part of a bigger picture, which includes similarity, inclusion, invariance and complementation. Such connections variously exist between sets of pitch-classes as they occur in music or between their abstract formulation as pcsets in prime form (expressed as integers); that is, as interperspective relationships of ‘pitch-class’ or ‘relative pitch-class’. This apparently fine distinction can be of considerable significance, since the effect of one type of relationship may run counter to that of the other.[136] Here, we examine an area where theorists have expended a good deal of effort: establishing indices of similarity through which differing pcsets can be compared.
There are two main levels at which such comparisons can be undertaken: pitch-classes and interval-classes. With regard to the former, Forte[137] proposes a maximum similarity relation RP between pcsets such that
RP (S1, S2) iff • (S3 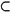
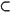
where sets S1, S2 are of cardinal number n and S3 is of cardinal number n–1. That is to say, sets S1 and S2 are maximally similar with respect to pitch-class if they differ with respect to only one element. As Forte observes, “RP is not especially significant since many sets are so related to a large number of other sets.”[138] In contrast, zygonic theory offers more responsive measures of pitch-class similarity between sets of all cardinalities. Two functions are possible: ZYG1 and ZYG1-SEQ.
ZYG1 expresses the proportion of all relationships between the members of two sets that are potentially primary zygons of pcset-pitch. In formal terms,
ZYG1 = #z / (#X • #Y)
In relationships between sets without repeated pitch-classes, values of ZYG1 tend to be low. For example:
Figure 35. Example of similarity index ZYG1 between manifestations of pcsets 5-Z37 and 5-28.
Even identical sets produce values that are relatively small, which reduce as the size of sets is increased, since the proportion of zygonic relationships is also smaller. See, for instance, Figure 36. While this may appear counterintuitive, consider that these pcsets are only a small part of a much larger universe, and ZYG1 values are markedly higher where there are repeated values. See, for example, Figure 37. Note that ZYG1 is at a maximum in comparing two repeated-value sets that are the same.
Figure 36. ZYG1 between identical pcsets diminishes with increasing cardinality.
Figure 37. Values of ZYG1 between sets with repeated pitch-classes.
However, closer to Forte’s notion of RP is the function ‘ZYG1-SEQ’, which entails one-to-one mapping between ordered sets of the same cardinality, such that the number of potential primary zygons (‘#z’) is taken as a proportion of the total number of primary interperspective relationships (including zygons) (‘#z + #i’, where ‘i’ are interperspective relationships between differing values). That is:
ZYG1-SEQ = #z / (#z + #i)
Hence ZYG1-SEQ exists in a range 0 to 1, where 0 represents complete dissimilarity (that is, no pcs in common), and 1 maximal similarity (all pcs the same). For example:
Figure 38. Example of ZYG-SEQ1.
The similarity of pcsets gauged through interval-classes has received more theoretical attention than judgements based on pitch-classes, and different approaches pertaining to ics have been summarised by Eric Isaacson (1990). Forte’s Rn relations indicate the match between corresponding terms in ic vectors. If none of the pairs is the same, the sets are in the relation R0. If all but two are the same, and the two unequal terms are ‘interchanged’, the sets are said to be in R1; if the unequal terms are not interchanged, then the sets are in R2.[139] As Isaacson notes,[140] Rn relations are limited in a number of respects: for example, they apply only to sets of the same cardinality; many pairs of ic vectors are in none of the Rn relations; Z-related sets are not categorised in terms of these relations (despite having identical ic content); and the relations lack discriminating power, having only three classes of similarity with which to categorise the thousands of possibilities that exist. These are theoretical difficulties with the Rn concept. However, zygonic meta-analysis reveals problems of a musical nature too.
Take, for example, the two sets 4-1 and 4-23 having ic vectors [321000] and [021030] respectively, and which, therefore, according to Forte, are in the relation R1. This implies a scenario such as the following.
Figure 39. Zygonic meta-analysis of example of relation R1.
In the case of ic2 and ic3, the measure of similarity is conceptually straightforward, and it may well be that the common primary relationships are, to a greater or lesser extent, highlighted in musical contexts. The potential relevance of ic4 and ic6 is less immediate – it is unclear whether shared absent intervals have any significance for listeners. Even more remote, though, are the ‘interchange’ relationships, whereby the fact that there are the same number of ic1s in 4-1 as there are ic5s in 4-23 and the same number of ic5s in 4-1 as there are ic1s in 4-23 is held to be a worthy measure of similarity. It is difficult to imagine a context in which numerical connections such as these could be of music-structural significance.
The remaining functions that Isaacson discusses operate through comparing like interval-classes, comprising variously aggregated forms of their differences, sums or products.[141] However, Isaacson identifies theoretical difficulties with all of these, in terms of the number, range and profile of the values they produce. Isaacson’s own ‘IcVSIM’ function takes the standard deviation of the values in an ‘Interval-difference Vector’, which lists the arithmetic differences between the respective entries in ic vectors. That is, IcVSIM measures the degree of variance found between the number of corresponding ics in two pcsets. It is formally defined as
where IdVi is the ith term of the Interval-difference Vector, and 
Zygonic theory offers an alternative approach to the issue of pcset similarity. Just as the internal ‘zygonicity’ of a pcset may be taken as the ratio of latent zygonic relationships to the number of potential relationships as a whole, so the zygonicity between pcsets can be calculated according to the same principle. That is to say, rather than comparing only identical ic entries in the two sets concerned, the ZYG2 function takes into account all prospective secondary relationships between the ics in different sets, whatever their entry number, and calculates the proportion that are potentially zygonic. It seems justifiable – indeed, necessary – to consider all relationships, since the ZYG2 measure is principally a conceptual one, between two abstract entities, whose perceived interconnections will differ according to the musical context in which they are realised.
In formal terms, the zygonicity between pcsets at the secondary level may be expressed as follows:
This formula works for sets of all cardinalities. For example,
That is, one third of the secondary relationships that link the two pcsets are potentially zygonic between identical primary values. For example:
Figure 40. ZYG2(3-1, 4-2) =
Secondary zygonicity is at a maximum when X = Y. For instance, ZYG2 (3-1, 3-1) = 0.556. Although this value may seem unduly low, consider that it merely reflects the totality of the differences and similarities between the two sets. Sets of identical pcs produce ZYG2 = 1. Take, for example, {0, 0, 0, 0} and {1, 1, 1}, whose primary ic vectors are [6. 0 0 0 0 0 0]1 and [3. 0 0 0 0 0 0]1 respectively: every secondary relationship between them is potentially a perfect zygon, so
At the other extreme, ZYG2 may = 0 if two sets share no ic entries in common: for example, 3-1 and 3-11. The full range of values for ZYG2 in relation to 3-1 are as follows.
Figure 41. Results for ZYG2(3-1, x-y).
ZYG2 represents one, wholly abstract, way of considering pcset similarity, free from the complicating factors that invariably arise in authentic musical contexts. While the function may have a certain validity as an ‘absolute’ measure – uncontaminated, for example, by perceived time or texture – it has to be recognised that it has very limited (if any) relevance to ‘typical’ listening experiences. For example, one realisation of a pcset may highlight a particular sequence of primary interperspective relationships while a second may bring quite another series to the fore, so emphasising the dissimilarities that exist within and between the sets (despite their theoretical equivalence). Hence, another measure is required that is sensitive to the sequential status of the relationships it compares. This may be termed ZYG2-SEQ, and functions as follows (cf. ZYG1-SEQ; Figure 38).
Figure 42. Example of relation ZYG2-SEQ.
The measures of zygonicity that have been identified, which consider either the internal orderliness of sets or the similarity between them, may be classified thus (see Figure 43).
Figure 43. ZYG and zyg functions in summary.
To summarise: this section has shown how zygonic theory can be used to interrogate other models of musical structure – in particular, set theory. The result is that refinements are proposed to certain established procedures (such as gauging the similarity between pcsets), while, on a more general level, issues are exposed in relation to the status of these and other processes. The key finding is this: since the pitch structure of any music that uses only twelve distinct pitch-classes is by its very nature highly constrained, it will inevitably be replete with potential orderliness – abounding with patterns that can be modelled mathematically. This is illustrated in the re-analysis of the opening of Schoenberg’s Op. 11, No. 1, which shows that every conceivable combination of relative pitch-classes (as defined by Allen Forte) is present in only the first 4½ bars; indeed, some appear hundreds of times. Hence it is argued that strictly logical approaches to music analysis, such as Forte’s system of ‘imbrication’, entailing the systematic extraction of pcsets, are fraught with difficulty, since they throw up unmanageable quantities of information, the great majority of which is of no relevance to the musical experience, perceptually or even, for the most part, conceptually. What, then, are the limiting factors that would render such approaches manageable and meaningful? The musical intuitions of the analyst – whose very subjectivity mathematical approaches were intended to capture, rationalise or even eradicate: these have to be the starting point and, ultimately, the criteria through which analyses are judged.
6. Taking a Zygonic Approach to Investigate Musical Interaction in Improvisation
The final extended example of zygonic theory in action occurs in the context of quantifying and analysing an example of musical interaction between a teacher and pupil, and considering its consequences for our understanding of the child’s level of musical development. The object of study is a vocal improvisation by ‘K’, a four-and-a-half-year-old girl with a condition known as septo-optic dysplasia,[144] which had previously been videoed and transcribed.[145] The improvisation was initially led and then accompanied on the piano by the author (‘AO’), who at the time was K’s music teacher. It is argued that the zygonic relationships that are identified between elements within the improvised duet provide powerful insights into the musical interaction between K and AO, capturing the fluctuating patterns of influence that existed between them as the piece they were creating unfolded in time.
The improvisation was triggered by AO suggesting to K that she should make up a new song about her pet dogs (Jack and Elisha). AO played four chords – F major, D minor, G minor9 and C major – on the piano with a gentle swing rhythm, and added a simple vocal melody to set the scene. After two iterations of the sequence, K intuitively took the lead and, against the continuing four-chord ostinato, improvised a song that lasted for around 90 seconds.
Figure 44. K’s improvisation I have a Dog
AO’s initial impression, as the teacher-accompanist, was of an extemporisation of genuine musical expressivity within a continuously evolving but coherent musical structure. It was clear that K had an active musical mind that was able to create new material intuitively, quickly and confidently within a broadly familiar style. Beyond these immediate reactions, however, the application of zygonic theory enables K’s improvisation to be analysed in relation to the three potential sources of material from which she could draw: (a) the unfolding melody, as initiated by AO and subsequently taken up by K; (b) the piano accompaniment provided by AO; and (c) other pieces in similar style.
So, considering first K’s melody: does it ‘make sense’ as a piece of music – and, if so, through what structural means? According to zygonic theory, musical coherence requires at least one salient feature from each event to derive from another or others.[146] A full zygonic analysis of K’s song (which is too extensive to be reproduced here)[147] shows that this is indeed the case, and confirms the informal observation that successive notes do not pass by as isolated entities, but sound logically connected to each other through similarities in pitch or rhythm which bind them together in the mind to form short melodic ‘chunks’. As we shall see, these chunks are themselves linked through various forms of sameness and similarity. Here, an analysis of K’s first phrase will suffice to illustrate the principles involved.
K’s song begins as she picks up on the fourth octave E that AO’s vocal line leaves in the air, and which is reinforced in his accompaniment. From here, K moves back to the adjacent F, following the change from tonic to dominant harmony, which she would have been able to anticipate from the same harmonic transition between bars 2 and 3. This opening melodic interval is a retrograde version of the ending of AO’s last vocal phrase – illustrating how, from the outset, K takes the material that is offered and stamps her authority on it. K’s initial F is followed by 11 others, together constituting a pitch structure of the simplest kind (potentially derived through a network of identical primary zygonic relationships that are known as a ‘constant system’; see Footnote 87). This repeated series of notes, which at first appears to overextend itself against the accompanying harmonies (conflicting with the concluding dominant chord in the second half of bar 6), could be heard as a device for K to buy time while deciding what to do next. However, analysis shows that the series of Fs actually grows organically from the preceding material, deriving from two sources: the pitches echo the initial repetitions of the melody, and the rhythm adopts the dotted-quaver/semiquaver pattern first heard in the second half of bar 2. This means that K took two distinct elements from the opening phrases of the melody (supplied by AO) and fused them in her continuation, a form of musical development typical of many styles that simultaneously offers coherence and variety.
Figure 45. K’s melody initially develops AO’s opening vocal line in a number of respects.
K’s forceful delivery of the repeated pitches adds to the sense that she is asserting her place in the partnership that is about to unfold: both musically and socially, building a foundation for the action to come. This starts immediately: in the very next phrase (bar 7), there is a sense of release as K’s melody springs up from the constraints of the opening repetitions using a new, syncopated rhythm. Despite the sense that things are moving off in a new direction, though, both pitch and rhythm again derive logically from what has gone before: the ‘dotted’ motive is again pressed into service and two similar ascending melodic intervals (from F to A, and A to C) deployed to straddle the phrases. This method of connecting chunks, through secondary zygonic relationships – rather like using a musical ‘ladder’ to link different ideas – is one that K adopts a number of times (for example, between bars 16/17 and 22/23). Her other favoured approach is to use a primary zygonic relationship – taking a pitch at or near the end of a phrase and using it to start the next (see, for example, the connections between phrases in bar 8, 18/19 and 20).
Figure 46. K connects melodic chunks through primary and secondary zygonic relationships.
These two approaches to connecting chunks of musical material are typical of many styles.[148] However, there is another way of linking segments, which involves the repetition (or variation) of chunks as a whole. Although, arguably, this is the most widespread of all music-structural techniques, it is not one that K adopts. The nearest she comes to it is in bars 17–24, when a pattern of three descending pitches is successively transposed and varied, mirroring and reinforcing the rhetorical form of the verbal narrative at this point: (“one for her biscuits, one for her water, and one for her meat”). Exact transposition of the intervallic descent, which would have required a 
Figure 47. On one occasion, K links melodic segments through the variation of chunks as a whole.
Why does K not make greater use of the commonplace method of repeating or varying chunks as a whole? It may be on account of the improvised nature of the exercise that K was undertaking, in which building a coherent structure depended on remembering material that had just been made up at the same time as continuing with the creative process (which may well have interfered with the memories that had recently been formed). By intuitively adopting the approach of having each successive chunk pick up where the previous one left off, K made fewer demands on her memory and gave herself greater freedom to follow her musical or verbal whim of the moment. A corollary of this free-flowing approach is that there is no particular pattern to the links between chunks in K’s song: while the moment-to-moment connections on the musical surface are convincing enough, there is no hierarchical arrangement of the segments – no deeper structural repetition or development. The climax, which occurs at the end of the improvisation, is signalled by a change of register and effected through a high, sustained tonic F (sung ‘fortissimo’), rather than occurring through a feeling of structural inevitability.
Hence, taking all this evidence into account, it is reasonable to assert that K had grasped a number of the key principles of how Western music (within the tonal vernacular of the early 21st century) is structured, and that she was able to use these to create new tunes that would make sense to listeners. We know that K developed this capacity with no formal intervention on the part of others – purely through being exposed to a range of music and through expressing herself by singing. Just as the great majority of people absorb the syntactical rules of their native language without conscious effort (simply by listening and trying things out for themselves), thereby acquiring the ability to create original but coherent and comprehensible linguistic utterances, so K evidently had done the same in the domain of music. Her intuitive awareness of certain elements of musical syntax within familiar styles enabled her to formulate new, stylistically authentic musical statements. Of course, this is not in itself exceptional; almost all young children make up songs that are coherent by absorbing, copying and extending what they hear, functioning as what Margaret Barrett terms infant ‘meme engineers’ (2003).[149] It is through considering the way in which the structural techniques that K employed interacted with the accompaniment that was provided that we can glean more about the unusual nature of her developing musicality.
Zygonic theory can be used to gauge the impact of the accompaniment on K’s creative efforts by assessing each note[150] in relation to its probable musical sources, which are to be found either in AO’s melodic opening (bars 1–4), the extemporised piano melody (equivalent to the uppermost RH notes), the bass ostinato or K’s vocal line.[151] For every note, up to 10 zygonic relationships[152] are considered in relation to pitch, melodic interval, harmonic context and rhythm. These are weighted as follows: pitch scores 2 for exact repetition and 1 for the transfer of pitch-class to a different octave; melodic interval scores 2 for identity, 1.5 for approximate imitation and 1 for inversion or retrogression; harmonic context scores 2 for exact repetition, 1.5 for variation, 1 for transposition and 0.5 for transposed variation; and rhythm scores 4 for identity, 3 for approximate derivation (including a change of relative location within the relevant metrical level), 2 for repetition of duration or IOI only, and 1 where the sole connection is the variation of duration or IOI. Since each aspect of every note could be considered to be derived from up to 10 others, further weighting is necessary, whereby each raw score of derivation strength is multiplied by a factor based on the theorised salience of the zygonic relationship concerned, such that the sum of the factors pertaining to the given feature of a particular note was invariably 1.
For example, K’s seventh pitch (labelled K7 in Figure 43) can be considered to derive from K6, K5, K4, AM13, K3, K2, AV12, AM11, AV11 and AM10 – the order determined by their temporal adjacency to K7.[153] For pragmatic reasons, the factors used to moderate the raw scores pertaining to series such as this are separated by a common difference (implying a linear decrease in the strength of their zygonic influence).[154] In this case, with ten factors required, the values used to modify the raw derivation scores are 0.182, 0.164, 0.145, 0.127, 0.109, 0.091, 0.073, 0.055, 0.036 and 0.018 respectively. The result of applying these proportions to the raw scores is a series of ‘derivation indices’.
The indices for each feature are summed separately in relation to the material improvised by AO and K. The total potential derivation index for each note ranges between 0 and 10 from either of the two sources (AO or K). With regard to K7, the subtotals pertaining to AO- and K-derived material are shown in Figure 47: pitch has a derivation index of 0.618 from AO and 1.382 from K; melodic interval, 0.334 from AO and 1.666 from K; harmonic context, 1.335 from AO and 0.666 from K; and rhythm, 1.620 from AO and 2.136 from K. This yields a total derivation index of 3.907 from AO’s material and 5.850 from K’s. Given the maximum total derivation index of 10, the sum of these two figures (9.757) leaves a residue of 0.243, reflecting aspects of K7 that cannot be accounted for through derivation from other material in the song. This, then, is a measure of the ‘originality’ of the event in question (K7) in relation to the improvisation up to that point.[155]
Figure 48. The hypothesised derivation of note ‘K7’ from previous material.
The usefulness of these figures in interpreting the relationship between AO’s and K’s contributions lies principally in the ratios between them – taken either as averages over a given period or in terms of event-by-event patterns of variation. For example, the derivation indices for the piece as a whole are as follows.
Figure 49. The sums of the derivation indices for I have a Dog taken as a whole.
That is to say, 70% of AO’s production was generated from other of his material, with a little under 13% deriving from K’s input. In contrast, only 50% or so of K’s melody is attributable to the emulation of her own efforts, with approximately 36% based on AO’s introductory vocal melody and piano accompaniment. This is powerful evidence that, while improvising her own structurally and expressively coherent melody, K was able to attend to the piano accompaniment and (apparently without conscious effort) take on board a range of musical ideas that were presented. Moreover, within the musical interaction that occurred, AO’s influence on K was almost three times greater than K’s impact on AO – a somewhat sobering statistic for a music educator who at the time felt that he was providing a responsive foil for K’s efforts! In fact, zygonic analysis indicates that the flow of musical ideas was largely from teacher to pupil. One wonders how asymmetrical the patterns of influence are in other more ‘typical’ music-educational and therapeutic contexts, notwithstanding teachers’ and therapists’ beliefs concerning the child-centeredness of their approaches.
The derivation indices also enable us to track how the influence of one performer on another varied over time. For example, during K’s first phrase (notes K1–K13), the derivation index from AO’s material falls from 9.476 to 0.927, whose trend closely matches a linear descent (R2 = 0.8155) – the principal exceptions being K9 and K10, where K introduces a rhythmic pattern similar to one used in AO’s introduction.
Figure 50. The waning influence of AO’s material in K’s first phrase.
This decline in K’s use of AO’s material through the phrase reflects K’s increasing self-assertion (noted above) and, as one would expect, is matched inversely by an increasing use of her own improvisation to generate further ideas. At the same time, K’s use of original material (‘Series 3’ in the graph) fluctuates at a low level.
Figure 51. Indices of derivation and originality.
Subsequent phrases show different derivational patterns that cannot be reported in detail here. However, the mean derivation indices pertaining to phrases will be used to give an overview of trends at a deeper structural level. These show K drawing significantly on A’s material in her first phrase, less so in the second and more again in the third and the fourth. Subsequently, there is a gradual decrease in AO’s impact over phrases five to nine – the central part of K’s improvisation with the descending sequence at its heart – during which K’s efforts become ever more self-sufficient. In contrast, AO’s influence is felt more strongly in K’s tenth phrase, whose lack of verbal coherence suggests that K may be running out of steam. Indeed, after rallying briefly in the eleventh phrase, K’s creative flow almost completely dries up at the beginning of the twelfth, and she draws heavily on material in the accompaniment to sustain her vocal line (although in the concluding notes she finally wrests back the initiative). K’s global pattern of derivation from AO, invariably lower than AO’s derivation from K, is inversely related to it with a striking consistency (82%). That is to say, during the improvisation, as K chose to rely less on AO for material, AO tended to rely more on K, and vice versa – perhaps through an intuitive desire on the part of one performer or both to ensure coherence in the improvised texture as a whole.
Figure 52. The inverse relationship between the strength of musical influence of AO upon K’s and vice versa throughout I have a Dog.
Analysing indices of ‘originality’ reveals further issues of structural significance. For example, itemising all K’s events that had an originality index 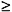
Figure 53. Table of K’s events with an originality index of 0.25 or more.
Although different features are implicated (including melodic interval, duration and interonset interval) K’s originality is most frequently expressed in the domain of harmonic context (in 62% of cases). On some occasions, this appears to be a consequence of K’s melodic intent overriding the harmony provided (for example, in the second half of bar 6 and at the end of bar 10), although her continuations make sense of these things in retrospect: as we have already observed, the repeated Fs in bar 6 serve as a springboard for the next phrase, while the F at the end of bar 10 is sustained to reach over into the F major harmony that starts the next sequence. However, there are other times when, rather than having arisen as a byproduct of melodic goals, K’s harmonic originality seems to have been intrinsically motivated; see, for example, K27, where K’s 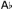
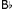
Despite the substantial impact of AO’s improvisation on K’s melody, the derivation is largely at a ‘general’ level, whereby each feature almost invariably stems from a number of sources, and the relationships concerned rarely have the salience to stand out from their coherence-creating neighbours and acquire specific structural significance. There are exceptions, however, which function either through a series of relationships working in parallel or by prominent percepts being repeated in temporal apposition. For example, the syncopated rhythm first heard in the piano in bar 12 reappears in the vocal melody in bar 15 (and then again in the piano in bar 24), while from bar 30, K repeatedly derives 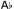
The third and final issue to be addressed is the extent to which K uses material from other pieces in her improvisation. For this to occur implies that the music improvised by AO (and by K herself) triggered features common to many other pieces – stylistic influences – that were subsequently pressed into service in the new work, or specific memories of other compositions, or both. Direct borrowing is not a requirement for musical coherence (although it is encountered widely in traditional jazz[157]), and it is not an approach that K adopts.[158] The utilisation of more general features is far more important in the construction of musically meaningful pieces, however, and K’s improvisation does indeed fit comfortably within the stylistic envelope of the Western musical vernacular of the late 20th and early 21st centuries, in terms of the tonal and rhythmic frameworks that are used. More than this, though, K utilises a range of melodic devices that indicate a certain musical sophistication, including passing notes (in bars 15 and 16) and appoggiaturas (see bar 25), as well as elements redolent of the Blues style, in particular the flattened third, first introduced in bar 10.[159]
In summary: in this section, we have analysed a vocal melody improvised by a young girl with septo-optic dysplasia against an ostinato piano accompaniment, using zygonic theory. From this, it appears that the zygonic approach may be of value in interrogating certain aspects of the ebb and flow of musical interaction involving two performers or more. Although labour-intensive at this stage, key elements in this type of analysis could be automated using an appropriate computer programme, leaving the researcher to check and refine the data gathered. The techniques set out here could be used more widely to support the assessment of certain aspects of children’s music-making informing the aggregation of a bank of comparative data that would enable individual efforts to be contextualised. Clearly, this may be of benefit to music therapists and educationists seeking to evaluate the effect and effectiveness of their interactions with children with disabilities and other special needs. Moreover, as music-analytical techniques such as those used here are further developed, it is interesting to postulate the extent to which the scrutiny of the purely musical elements of an improvisation with two people or more may shed light on aspects of broader personality and human relationships – including the capacity and willingness for imitation, resistance to change, resilience and so on. More broadly, the approach set out here may support the analysis of improvised forms in a range of genres, including jazz.
There are also findings of significance in relation to K’s evolving musicality. For example, it is evident that, within a familiar style, she can grasp a repeating pattern of harmonies and create material that not only conforms to what is provided but develops and extends it, structurally and expressively. However, there is a lack of thematic correspondence between voice and accompaniment that may have arisen as a consequence of the considerable musical skill and experience that are needed to attend to someone else’s contribution and remember it at the same time as creating material oneself. More broadly, the fact that certain common approaches to the logical connection of material are not used, and the concomitant absence of a deeper structure may be specific to this improvisation or could indicate where future avenues of K’s learning may lie. Above all, though, K’s improvisation provides evidence that many of the elements of musical understanding, which are typically conceptualised and codified in the process of music education, can develop and thrive at a purely intuitive level. The enduring message for researchers and teachers alike is the capacity of the mind to absorb and intuitively utilise sophisticated musical strategies with no formal tuition at all.
Epistemological Issues and Future Prospects for Zygonic Theory
It is hoped that these three extended examples will give readers who were previously unfamiliar with zygonic theory some idea of its scope and potential applications. As well as offering new concepts, new methods, new tools and new forms of graphical representation to music theorists and analysts (or, indeed, to those working more broadly within the field of musicology) perhaps zygonic theory’s most significant contribution will be to those researchers seeking to work between disciplines, where music theory and analysis meet music education and music therapy, for example, and – especially – music psychology. Here, two decades on from Eric Clarke’s appeal to ‘Mind the Gap’ (1989), there are still considerable epistemological hurdles to be overcome if the two disciplines are to work together effectively,[160] and it may be that further developments will mean both parties having to accept that the initial research questions and the evaluation of data will be guided by musical intuitions, but that the gathering and analysis of data will be rigorous and undertaken with a ‘scientific’ detachment. Today, this conceptual intersection is at least recognised and has a name: ‘empirical musicology’, which, according to Honing (2006), “grew out of a desire to ground theories on empirical observation and to construct theories on the basis of the analysis and interpretation of such observations”. As Cook and Clarke put it: “Empirical musicology … can be thought of as musicology that embodies a principled awareness of both the potential to engage with large bodies of relevant data, and the appropriate methods for achieving this”.[161] One senses that in this sphere of activity that zygonic theory may most naturally find a future home.
Notes
By coincidence, the year in which I was working on my arrangement of O Waly, Waly (1983) was the year in which Allan Forte first published his analysis of Brahms’s String Quartet in C minor – in which he identifies the key role of the motive (+2, +1) and its three isomorphic derivatives. (See also Huron’s 1998 critique of Forte’s analysis.) | |
Fred Lerdahl’s paper on the possible conflicts between ‘compositional’ and ‘listening’ grammars was still some way off (1992). | |
Meyer 1973, 44. | |
See, for example, Cohen 1962. | |
See also Nattiez 1990; 1998. | |
Ruwet 1966 – English translation 1987, 16. | |
Lerdahl and Jackendoff 1983, 52. | |
Schönberg considered the motive to the ‘smallest common multiple’ and the ‘greatest common factor’ in music (1967, 8). | |
Taken from the earlier French melody ‘Ah vous dirais-je, Maman’, upon which Wolfgang Amadeus Mozart wrote a set of variations (K. 265/300e). | |
Cone 1987, 237. | |
Eliot [1920] 1997, 85. | |
Eliot 1933, 118 –9. | |
Ockelford 2005b, 84. | |
Cf. Johnson-Laird and Oatley 1992, 20; Sparshott 1994, 28. | |
See, for example, Juslin, Friberg and Bresin 2001–2. | |
Scherer, Banse and Wallbott 2001. | |
That is, through evolution of a species. | |
Scherer 1991. | |
Through the development of an individual. | |
Malloch 1999–2000; Trehub and Nakata 2001–2. | |
Gabrielsson and Lindström 2001. | |
Watson 1942. | |
Scherer and Oshinsky 1977. | |
Watson 1942. | |
Thompson and Robitaille 1992. | |
Gundlach 1935. | |
Balkwill and Thompson 1999. | |
Watson 1942. | |
Gundlach 1935. | |
Nielzén and Cesarec 1982. | |
Juslin 1997. | |
Meyer 2001. | |
London 2001–2. | |
Meyer 2001, 342. | |
Krumhansl 1997; Peretz, Gagnon and Bouchard 1998. | |
Jariazbhoy 1971. | |
Hevner 1936; Crowder 1985. | |
Bregman 1990. | |
Cf. Selincourt [1920] 1958. | |
See also Meyer 1989, 84ff. | |
Such as the ‘continuity illusion’, summarised in Bregman 1990, 344ff. | |
For instance, DeWitt and Samuel 1990. | |
Ockelford 1999. | |
See Zbikowski 1998; 2002. Building on the work of George Lakoff, Zbikowski shows how such notions are underpinned by culture-specific conceptual metaphors, mapped onto the domain of music-space from our perception of the physical world. | |
See Ockelford 2002. | |
See Euguene Narmour’s discussion of musical expectations by cognitive rule-mapping (2000, 364). | |
Ockelford 1993. | |
Ockelford 1999. | |
Ockelford 2005a. | |
Ockelford 1999; 2005a. | |
Ockelford 2005b. | |
Ockelford 2009. | |
Ockelford 2005a. | |
Ockelford 2005a. See, for example, Lewin 1987. | |
Ockelford, forthcoming 1. | |
Ockelford 2002. | |
Ockelford 2004. | |
Ockelford 2006a; 2008b. | |
Ockelford and Pring 2005. | |
Ockelford 2007b. | |
Ockelford forthcoming, 2. | |
Ockelford 2006b; 2007a. | |
Ockelford and Himonides, forthcoming. | |
Ockelford, Welch, Zimmermann and Himonides 2005; Ockelford 2008a. | |
Ockelford 2008d. | |
Ockelford 1999; 2005b. | |
Ockelford 2005a. | |
Ockelford 2007. | |
The sonata is thought to have been composed in the summer of 1783, in Linz and Vienna – see, for example, Tyson 1987; Mercado 1992. | |
Meyer 1973, 6ff. | |
Cf. Boulez 1971, 37; Sharpe 1983, 274–86. | |
Analysis of a range of recordings of performances of the first movement of K. 333 reveals the following tempi: Andreas Schiff (1981) Decca (443 717-2) | |
That is, between pieces. | |
For example, in the recordings of Eschenbach (1971), IOIs between successive notes exist in K. 330 within the range | |
This analysis and those that immediately follow use the concept of perceptual ‘streams’ of sound – discrete linear strands in the musical texture – of which the first movement of K. 333 utilises two (delineated by the RH and LH parts). Each may contain ‘harmonic blends’ (comprising two simultaneous notes or more), which are treated as single temporal events. | |
For example, K. 284, first movement utilises eight different durations; K. 310, first movement makes use of eleven; and K. 311 employs nine. | |
Fraisse 1978, 243. | |
Dissimilarity calculated as the sum of the average divergence from the mean in each (durational) category. Hence: where xi is the value of a given (durational) category in a piece, n is the number of pieces, and the sum of different categories under consideration in a piece = 100%. | |
Moreover, since the perceived temporal interval between adjacent onsets tends to correspond to the duration pertaining to the first, it is most probable that a duration will be succeeded by another one the same. | |
Ockelford 2006. | |
See, for example, Fucks 1962, Jeffries 1974, Dowling 1978, Huron 2006. | |
Shepard 1982, 376. | |
For example, Bregman and Campbell 1971. | |
Spender 1983, 280. | |
Ockelford 2006a. | |
Indeed, it is generally acknowledged that tertian harmonies form the basis of all chords used in Western music in the period 1450–1900 (Apel 1969, 373 and 374), as well as in the music of many other cultures, where comparable constraints are to be found – see, for instance, Eta Harich-Schneider’s 1953 account of Japanese Court Music. | |
A ‘zygonic constant system’ is a network of potential relationships (any or all of which may be active in the creation or cognition of musical structure) linking features that are the same – see Ockelford 2005a. | |
Gauged with respect to local tonal regions. Hence absolute values may differ within a category. | |
See Ockelford 1999. | |
That is, their position within the bar. | |
See Berry [1966] 1986; Rosen 1971; 1980. | |
See also the others identified in Ockelford 1999. | |
Roe 1989. | |
Einstein 1946, 130–1. | |
See Ockelford 1999. | |
There are, of course, a host of extramusical reasons why some pieces become established and others fail to thrive. | |
Réti 1951, 4. | |
Réti 1973, 64ff. | |
Réti 1967, 26. | |
Meyer 1956, 210. | |
Meyer 2001, 357. | |
Ockelford 2005b. | |
Up to a point, at least – see, for example, Smith and Cuddy 1986, 17–32; Gaver and Mandler 1987, 259–82. | |
Ockelford 2008b. | |
See Ockelford 1999, 539–41: “An additional pitch (or more than one) is commonly used to bridge the gap separating two values ...” These may be derived zygonically in the following way. “In perceiving tunes, listeners tend to hear not a series of pitches – each a discrete entity in its own right – but a single value that, with the passing of time, apparently occupies different positions in the perspective domain. With this model of perception, it is less appropriate to think of an interval between adjacent [pitches] … as the difference between two separate notes than as the silent expression of the imagined movement of a pitch from one location to another. This implies that, in their apprehension of intervals, listeners must mentally sweep over the range of perspective values outlined by successive pitches. Any of the values thus imagined can subsequently be realized in sound through zygonic relationships. This can be shown diagrammatically with a square bracket linking the [notes] … whose vacant connecting interval is filled on a subsequent occasion. A primary zygonic constant leads from this to the newly created pitch [or pitches].” This notion is derived from Meyer 1973, 144: “A disjunct interval may be understood as a kind of incompleteness – a gap – that implies that the note or notes skipped over will be presented in what follows.” | |
The cognitive relevance of these potentially competing structural interpretations may (we may surmise) vary from listener to listener and from one occasion to another. | |
Compare with the use of the subdominant at this point in Bach’s Op. 5, No. 3. | |
I discuss the potential aesthetic effect of minor harmonies in a major context and vice versa in Ockelford 2005b. | |
Again, compare with Op. 5, No. 3, in which a similar pattern of statement and response is underpinned with comparable forms of organisation – but here the relationships are far more straightforward. | |
See Forte 1973 and Rahn 1980 for early summaries. | |
Dunsby 1998, 177. | |
Forte 1988. | |
Adapted from Meyer and Shreffler 1993. | |
See Morris 1997, 276. | |
E.g., Bruner 1984. | |
See e.g. Walsh 1984; Cook 1994; Gjerdingen 1999; Ockelford 2008d. | |
Forte 1973, 86ff. | |
Tertiary interval classes (‘ic3’s) and those of higher ranks are theoretically conceivable, too. | |
For completeness, ic1 vectors can be written in this form too. Hence, the vector for 4-25 would appear [0.020202]1. | |
Few sets bear no potential secondary zygons. They are: 3-2, 3-3, 3-4, 3-5, 3-7, 3-8, 3-11, 4-Z15 and 4-Z29. That is, four pcs is the most that it is possible for a composer to select without implying some inherent orderliness at the secondary level. (Note that all sets of cardinality 4 have some internal zygonic connection at the tertiary level.) This zygonicity forms part of the ‘background’ order that is inevitable in choosing pitch-classes from a highly constrained universal set. Clearly, a key analytical judgement is which zygonic relationships were designed by the composer to function structurally, and which quasi-structural relationships arise by chance from the limited framework of pitch that is used. | |
Alternative measures of orderliness are given by the functions zyg1-seq and zyg2-seq, which take into account only those relationships between adjacent members of a set. Hence they may be particularly appropriate in evaluating the structure of series (i.e., ordered successions) of pcs. For example, the excerpt shown in Figure 40, the pcset is 4-12, prime form {0236}, ic1 vector [0.112101]1 and ic2 vector [1.543110]2. Hence zyg1 = 0 and zyg2 = 0.067. However, zyg1-seq = 4 / 9 = 0.444, and zyg2-seq = 3 / 8 = 0.375. | |
Note that the chromatic scale has a zyg2-seq value of 1. | |
Forte 1973, 83. | |
Forte 1998, 243. | |
See, for example, Forte 1998 and Doerksen 1998. | |
Forte 1973, 83. | |
Ockelford 2004. | |
Forte 1973, 83. | |
See e.g. Roeder 1988. | |
Interestingly, Forte himself raises the issue of the usefulness and validity of mechanical processes in analysis, as opposed to human engagement that requires “education, experience, and … cognition” (1998, 243). | |
Forte 1981, 140. | |
This compares with the amount of ‘background’ organisation identified in relation to the first movement of K. 333. This, however, pertains to different characteristics of perceived sound, which appear to make the processing load manageable. | |
The number of combinations is so great because, as Figure 33 indicates, the chords offer multiple ‘routes’ through the excerpt – a characteristic of which Forte himself takes advantage, as Figure 30 shows. To put the statistics in context, consider that a series of 22 notes that is purely melodic in nature harbours 7(n – 5) = 119 pcsets (3 _ cardinality _ 9) – ignoring the possible effects of repetition: a tiny fraction of the number identified in the opening of Op. 11, No. 1, but far too great a load for human cognitive faculties to bear, nonetheless. | |
The statistics presented here do, however, inform our understanding of the relative probability of occurrence of pcsets of different cardinalities. In his ‘Fortenotes’ (1998), Jonathan Dunsby observes (178): “In his 1988 article Forte at last publicly addressed the issue of probability … by means of an index termed a status quotient [‘squo’]. … Probability was always a niggle-and-a-half in respect of the Structure of Atonal Music. How can 50 hexachords survive the onslaught of 12 trichords? Every time a hexachord is … ‘found’, it is just that much less likely to be … found in comparison with any particular trichord, which has a 1 in 12 chance of appearing among the universe of normal trichords, a lot better than 1 in 50, which is the natural selection field of the hexachords. Or you can turn the probability issue onto its other head, and say that any particular hexachord is more important as a musical instance, because it is statistically less likely to appear than is any particular trichord.” Yet in typical ‘two-dimensional’ musical textures such as that of Op. 11, No. 1, systematic segmentation reveals the incidence of pcsets rising with cardinality. That is, there are far more occurrences of hexachords than trichords, in the ratio of the order of 1:40. This far outweighs the fact that the ratio of trichords to hexachords is of the order of 1:4. Hence the probability of a particular trichord occurring as opposed to a given hexachord is of the order of 0.1. | |
103ff. | |
Ibid., 97. | |
Forte 1973, 47. | |
Forte 1973, 48. | |
Forte 1973, 48 and 49. | |
Isaacson 1990, 3 and 4. | |
The functions are from Teitelbaum (1965), Morris (1979–80), Rahn (1979–80), Lewin (1979–80) and Lord (1981). | |
Isaacson 1990, 25. | |
Isaacson 1990, 21 and 22. | |
Septo-optic dysplasia is a rare condition that occurs in approximately 1 in 16,000 children. It is defined as a combination of optic nerve hypoplasia (absent or small optic nerves), pituitary abnormalities and the absence of the septum pellucidum or corpus callosum or both – without which communication between areas of the mid-brain (such as the transfer of sensory information) is hampered. Among the likely effects of septo-optic dysplasia are visual impairment, hormonal problems, delayed development, behavioral difficulties and obesity. The type and range of symptoms can vary from mild to very severe (Mehta and Dattani 2004). It is important to note that K is totally blind and does not have delayed development. | |
See Ockelford, Pring, Welch and Treffert 2005; Ockelford 2006b; 2007a. | |
That is not to say that, in order to be coherent, K’s improvisation should consist only of repetition. Through ‘perceptual binding’ (the cognitive glue through which the different properties of an object cohere in the mind to form the notion of a single thing – see, for example, Snyder (2000, 7)) and Gestalt perception (through which discrete events are reckoned to form larger wholes – see, for instance, Deutsch (1999)) sounds, or groups of sounds, may differ from each other in some respects while being the same in others. Hence (as we shall see), similarity and diversity work in parallel in the creation of musical material that is at once original though coherent. | |
Fuller presentations of data and their analysis are available in electronic form from the author. | |
Ockelford 2004. | |
See also, for example, Moog 1969; Hargreaves 1985, 60ff); Barrett 2006. | |
Hence the analysis is as fine-grained as it is practicable to make it. Longer pieces could be investigated using more substantial musical gestures as the primary unit of analysis. | |
This work was undertaken by AO, utilising his intuitions as an experienced music analyst, performer and educator. The principal disadvantage of this approach was the possibility of bias through idiosyncratic interpretation of the underlying structural relationships. The advantage was his intimate knowledge of the situation in question – in particular what was going through his mind as the accompanist. Future analyses along these lines could (though need not) be based more on the consensus of a number of people’s views. Indeed, it is anticipated that a significant proportion of the analytical activity could be undertaken by computer (searching for combinations of similarity and salience through appropriate algorithms). | |
Chosen for pragmatic reasons – other analyses could involve more or fewer relationships per feature than this. | |
On the grounds that, other things being equal, their temporal adjacency corresponds to their relative salience and therefore implicative strength. Factors that could impact on this assumption include the possibility of an event pertaining to a larger perceptual unit. Hence it is thought that the bass note at the beginning of bar 5 (third octave F), for example, more strongly derives from the bass notes at the beginning of bars 3 and 1 respectively than the temporally more adjacent Fs in the vocal and piano melody lines (something that is reinforced through common and differing octaves respectively). | |
Future analyses could adopt different approaches. | |
The issue of material derived from other pieces is considered briefly in the third section of the analysis. | |
Similarly, while K’s phrase-lengths indicate her evident cognisance of the underlying harmonic structure, they are not bound by it, ranging in duration from two beats to nine. Here, the influence of the improvised words appears to have been particularly important. Moreover, in the manner of a mature musical dialogue, K sometimes left the piano to play on its own (notably in bars 11 and 12), partly to regroup her own thinking, no doubt, though nonetheless affording a convincing feeling of ‘give and take’. | |
See Berliner 1994, 103ff. | |
AO does, however, quoting Dream, Dream, Dream by the Everly Brothers in bars 20–23. | |
Although this is hinted at by AO in bars 5 and 6. | |
See, for example, Mailman 2007; Ockelford 2009. | |
Cook and Clarke 2004, 5. |
References
Balkwill, Laura-Lee, and William Forde Thompson. 1999. “A Cross-Cultural Investigation of the Perception of Emotion in Music: Psychophysical and Cultural Cues.” Music Perception 17.1: 43–64.
Barlow, Harold, and Sam Morgenstern. 1948. A Dictionary of Musical Themes. London: Faber and Faber.
Barrett, Margaret. 2003. “Meme Engineers: Children as Producers of Musical Culture.” International Journal of Early Years Education 11.1: 195–212.
–––. 2006. “Inventing Songs, Inventing Worlds: the ‘Genesis’ of Creative Thought and Activity in Young Children’s Lives.” International Journal of Early Years Education 14.1: 201–20.
Berliner, Paul F. 1994. Thinking in Jazz: The Infinite Art of Improvisation. Chicago: The University of Chicago Press.
Berry, Wallace. [1966] 1986. Form in Music. Second edition. Englewood Cliffs, New Jersey: Prentice-Hall.
Boulez, Pierre. 1971. Boulez on Music Today. Cambridge, Massachusetts: Harvard University Press.
Bregman, Albert S. 1990. Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, Massachusetts: MIT Press.
Bregman, Albert S. and Jeffrey Campbell. 1971. “Primary Auditory Stream Segregation and Perception of Order in Rapid Sequences of Tones.” Journal of Experimental Psychology 32: 244–49.
Bruner, Cheryl L. 1984. “The Perception of Contemporary Pitch Structures.” Music Perception 2: 25–39.
Clarke, Eric. 1989. “Mind the Gap: Formal Structures and Psychological Processes in Music.” Contemporary Music Review 3: 1–13.
Cohen, Joel E. 1962. “Information Theory and Music.” Behavioural Science 7: 137–63.
Cone, Edward T. 1987. “On Derivation: Syntax and Rhetoric.” Music Analysis 6: 237–55.
Cook, Nicholas. 1994. “Perception: a Perspective from Music Theory.” In Musical Perceptions. Edited by Rita Aiello and John Sloboda. Oxford: Oxford University Press, 64–95.
Cook, Nicholas, and Eric Clarke, eds. 2004. Empirical Musicology: Aims, Methods, Prospects, Oxford: Oxford University Press.
Crowder, Robert G. 1985. “Perception of the Major/Minor Distinction: III. Hedonic, Musical, and Affective Discriminations.” Bulletin of the Psychonomic Society 23: 314–6.
Deutsch, Diana. 1999. “Grouping Mechanisms in Music.” In The Psychology of Music. Edited by Diana Deutsch. Second edition. New York: Academic Press, 299–348.
DeWitt, Lucinda A., and Arthur G. Samuel. 1990. “The Role of Knowledge-Based Expectations in Music Perception: Evidence from Musical Restoration.” Journal of Experimental Psychology: Genera 119: 123–44.
Doerksen, John F. 1998. “Set-Class Salience and Forte’s Theory of Genera.” Music Analysis 17: 195–205.
Dowling, W. Jay. 1978. “Scale and Contour: Two Components of a Theory of Memory for Melodies.” Psychological Review 85: 341–54.
Dunsby, Jonathan. 1998. “Fortenotes.” Music Analysis 17: 171–81.
Einstein, Alfred. 1946. Mozart: His Character, His Work. Translated by A. Mendel and N. Broder. London: Cassell and Co.
Eliot, Thomas S. [1920] 1997. The Sacred Wood: Essays on Poetry and Criticism. London: Faber and Faber.
–––. 1933. The Use of Poetry and the Use of Criticism. London: Faber and Faber.
Forte, Allen. 1973. The Structure of Atonal Music. New Haven: Yale University Press.
–––. 1981. “The Magical Kaleidoscope: Schoenberg’s First Atonal Masterwork, Op. 11, No. 1.” Journal of the Arnold Schoenberg Institute, 5: 127–68.
–––. 1983. “Motivic Design and Structural Levels in the First Movement of Brahms’s String Quartet in C Minor.” The Musical Quarterly 69.1: 471–502; reprinted in Brahms 2: Biographical, Documentary and Analytic Studies. Edited by Michael Musgrave. Cambridge: Cambridge University Press, 1987: 165–96.
–––. 1998. “Afterword.” Music Analysis 17: 241–4.
Fucks, Wilhelm. 1962. “Mathematical Analysis of the Formal Structure of Music.” Institute of Radio Engineers Transactions on Information Theory 8: 225–8.
Gabrielsson, Alf, and Erik Lindström. 2001. “The Influence of Musical Structure on Emotional Expression.” In Music and Emotion: Theory and Research. Edited by Patrick N. Juslin and John A. Sloboda. Oxford: Oxford University Press, 223–48.
Gaver, William W., and George Mandler. 1987. “Play it Again, Sam: on Liking Music.” Cognition and Emotion 1: 259–82.
Gjerdingen, Robert O. 1999. “An Experimental Music Theory?” In Rethinking Music. Edited by Nicholas Cook and Mark Everist. Oxford: Oxford University Press, 161–70.
Gundlach, Ralph H. 1935. “Factors Determining the Characterization of Musical Phrases.” American Journal of Psychology 47: 624–44.
Hargreaves, David J. 1986. The Developmental Psychology of Music, Cambridge: Cambridge University Press.
Harich-Schneider, Eta 1953. “The Present Condition of Japanese Court Music.” The Musical Quarterly 39: 49–74.
Hevner, Kate 1936. “Experimental Studies of the Elements of Expression in Music.” American Journal of Psychology 48: 246–68.
Honing, Henkjan. 2006. “On the Growing Role of Observation, Formalization and Experimental Method in Musicology.” Empirical Musicology Review 1.1: 2–6.
Huron, David. 1998. “What is a Musical Feature? Forte’s Analysis of Brahms Opus 51, No. 1 Revisited.” The 1999 Ernest Bloch Lectures, Berkeley: University of California. Available at
http://musiccog.ohio-state.edu/Music220/Bloch.lectures/Bloch.lectures.html
–––. 2006. Sweet Anticipation: Music and the Psychology of Expectation. Cambridge, Massachusetts: MIT Press.
Isaacson, Eric J. 1990. “Similarity of Interval-Class Content Between Pitch-Class Sets: the IcVSIM relation.” Journal of Music Theory 34: 1–27.
Jairazbhoy, Nazir 1971. The Ragas of North Indian Music. Middletown: Wesleyan University Press.
Jeffries, Thomas B. 1974. “Relationship of Interval Frequency Count to Ratings of Melodic Intervals.” Journal of Experimental Psychology 102: 903–5.
Johnson-Laird, Philip N., and Keith Oatley. 1992. “Basic Emotions, Rationality, and Folk Theory.” Cognition and Emotion 6.1: 201–23.
Juslin, Patrik N. 1997. “Perceived Emotional Expression in Synthesized Performances of a Short Melody: Capturing the Listener’s Judgement Policy.” Musicae Scientiae 1.1: 225–56.
Juslin, Patrik N., Anders Friberg, and Roberto Bresin. 2001–2. “Toward a Computational Model of Expression in Music Performance: the GERM Model.” Musicae Scientiae, Special Issue: Current Trends in the Study of Music and Emotion: 63–122.
Krumhansl, Carol. 1997. “An Exploratory Study of Musical Emotions and Psychophysiology.” Canadian Journal of Experimental Psychology 51: 336–52.
Lerdahl, Fred. 1992. “Cognitive Constraints on Compositional Systems.” Contemporary Music Review 6.1: 97–121.
Lerdahl, Fred and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. Cambridge, Massachusetts: MIT Press.
Lewin, David. 1979–80. “A Response to a Response: On Pcset Relatedness.” Perspectives of New Music 18: 498–502.
–––. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University Press.
London, Justin. 2001–2. “Some Theories of Emotion in Music and Their Implications for Research in Music Psychology.” Musicae Scientiae, Special Issue: Current Trends in the Study of Music and Emotion: 23–35.
Lord, Charles H. 1981. “Intervallic Similarity Relations in Atonal Set Analysis.”Journal of Music Theory 25: 91–111.
Macpherson, Stewart 1915. Form in Music. London: Joseph Williams Ltd.
Mailman, Joshua B. 2007. “Review Article: A. Ockelford, Repetition in Music: Theoretical and Metatheoretical Perspectives.” Psychology of Music 35.1: 363–75.
Malloch, Stephen N. 1999–2000. “Mothers and Infants and Communicative Musicality.” Musicae Scientiae, Special Issue: Rhythm, Musical Narrative and Origins and Human Communication: 29–57.
Mehta, Ameeta, and Mehul Dattani. 2004. “Clinical Aspects of Septo-Optic Dysplasia.” Eye Contact 38: 5–7.
Mercado, Mario R. 1992. The Evolution of Mozart’s Pianist Style. Carbondale, Illinois: Southern Illinois University Press.
Meyer, Felix, and Anne C. Shreffler. 1993. “Webern’s Revisions: Some Analytical Implications.” Music Analysis 3: 355–79.
Meyer, Leonard B. 1956. Emotion and Meaning in Music. Chicago: The University of Chicago Press.
–––. 1967. Music, the Arts, and Ideas. Chicago: The University of Chicago Press.
–––. 1973. Explaining Music. Chicago: The University of Chicago Press.
–––. 1989. Style and Music Theory, History and Ideology. Philadelphia: University of Pennsylvania Press.
–––. 2001. “Music and Emotion: Distinctions and Uncertainties.” In Music and Emotion: Theory and Research. Edited by Patrik N. Juslin and John A. Sloboda. Oxford: Oxford University Press: 341–60.
Moog, Helmut 1969. Das Musikerleben des vorschulpflichtigen Kindes: Grundfragen der allgemeinen Musikpsychologie. Mainz: Schott.
Morris, Robert D. 1979–80. “A Similarity Index for Pitch-Class Sets.” Perspectives of New Music 18: 445–60.
–––. 1997. “K, Kh, and Beyond.” In Music Theory in Concept and Practice. Edited by James M. Baker, David Beach, and Jonathan W. Bernard. New York: University of Rochester Press: 275–306.
Narmour, Eugene. 2000. “Music Expectations by Cognitive Rule-Mapping.” Music Perception 17.1: 329–98.
Nattiez, Jean-Jacques. 1990. Music and Discourse: Toward a Semiology of Music. Translated by C. Abbate. Princeton, New Jersey: Princeton University Press.
–––. 1998. “Le solo de cor anglais de Tristan und Isolde: essai d’analyse sémiologique tripartite.” Musicae Scientiae, Special Issue: An interdisciplinary approach: five authors in search of a subject – Tristan und Isolde, ‘cor anglais’ solo: 43–62.
Nielzén, Soren, and Zvonimir Cesarec. 1982. “Emotional Experience of Music as a Function of Musical Structure.”Psychology of Music 10.1: 7–17.
Ockelford, Adam. 1993. “A Theory Concerning the Cognition of Order in Music.” Unpublished PhD dissertation, The University of London.
–––. 1999. The Cognition of Order in Music: A Metacognitive Study. London: Roehampton Institute.
–––. 2002. “The Magical Number Two, Plus or Minus One: Some Limitations on our Capacity for Processing Musical Information.” Musicae Scientiae 6: 177–215.
–––. 2004. “On Similarity, Derivation and the Cognition of Musical Structure’.”Psychology of Music 32.1: 23–74.
–––. 2005a. Repetition in Music: Theoretical and Metatheoretical Perspectives, London: Ashgate.
–––. 2005b “Musical Structure, Content and Aesthetic Response: Beethoven’s Op. 110.” Journal of the Royal Musical Association 129.1: 74–118.
–––. 2006a. “Implication and Expectation in Music: a Zygonic Model.” Psychology of Music 34.1: 81–142.
–––. 2006b. “Using a Music-Theoretical Approach to Interrogate Musical Development and Social Interaction.” In Sounding Off: Theorizing Disability in Music. Edited by Neil Lerner and Joseph N. Straus. New York: Routledge: 137–155.
–––. 2007a. “Exploring Musical Interaction Between a Teacher and Pupil, and Her Evolving Musicality, Using a Music-Theoretical Approach.” Research Studies in Music Education 28: 3–23.
–––. 2007b. “A Music Module in Working Memory? Evidence from the Performance of a Prodigious Musical Savant.” Musicae Scientiae, Special Issue: Performance Matters: 5–36.
–––. 2008a. Music for Children and Young People with Complex Needs. Oxford: Oxford University Press.
–––. 2008b. Review Article: “D. Huron, Sweet Anticipation: Music and the Psychology of Expectation.” Psychology of Music 36.3: 367–382.
–––. 2009. “Similarity relations between groups of notes: Music-Theoretical and Music-Psychological Perspectives.” Musicae Scientiae, Special Issue on Similarity.
–––. 2008d. “Beyond Music Psychology.” In Oxford Handbook of Music Psychology. Edited by Susan Hallam , Ian Cross, and Michael Thaut. Oxford: Oxford University Press: 539–551.
–––. (forthcoming 1) “Constructing Meaning When Words and Music are Blended: A Zygonic Analysis of Dido’s Lament by Henry Purcell.”
–––. (forthcoming 2) “Hierarchy and Prolongation in Music: A Zygonic Investigation.”
Ockelford, Adam, and Evangelos Himonides. Forthcoming. “The Realisation of Musical Content and Structure in Performance: Exploring Interpretations of Henry Purcell’s Dido’s Lament.”
Ockelford, Adam, and Linda Pring. 2005. “Learning and Creativity in a Prodigious Musical Savant.” In Proceedings of International Society for Low Vision Research and Rehabilitation Conference 2005, International Congress Series 1282, 903–7, Amsterdam: Elsevier.
Ockelford, Adam, Linda Pring, Graham Welch, and Darold Treffert. 2005. Focus on Music: Exploring the Musical Interests and Abilities of Blind and Partially-Sighted Children with Septo-Optic Dysplasia. London: Institute of Education.
Ockelford, Adam, Graham Welch, Sally Zimmermann, and Evangelos Himonides. 2005. “Mapping Musical Development in Children with PMLD: the ‘Sounds of Intent’ Project.” SLD Experience 43: 20–3.
Peretz, Isabelle, Lise Gagnon, and Bernard Bouchard. 1998. “Music and Emotion: Perceptual Determinants, Immediacy, and Isolation after Brain Damage.” Cognition 68: 111–41.
Rahn, John. 1979–80. “Relating Sets.”Perspectives of New Music 18: 483–98.
–––. 1980. Basic Atonal Theory. New York: Longman.
Réti, Rudolph. 1951. The Thematic Process in Music. Connecticut: Greenwood Press.
Roeder, John. 1988. “A Declarative Model of Atonal Analysis.” Music Perception 6: 21–34.
Roe, Stephen. 1989. Keyboard Music: Thirty-Five Works from Eighteenth-Century Manuscript and Printed Sources, New York: Garland Publishing.
Rosen, Charles. 1971. The Classical Style. London: Faber and Faber.
–––. 1980. Sonata Forms. New York: W.W. Norton and Co.
Rosner, Burton S., and Leonard B. Meyer.1986. “The Perceptual Roles of Melodic Process, Contour and Form.” Music Perception 4.1: 1–40.
Ruwet, Nicolas. [1966] 1987. “Methods of Analysis in Musicology.” Translated by M. Everist, Music Analysis 6: 3–36.
Schenker, Heinrich. 1906. Harmonielehre (Neue musikalische Theorien und Phantasien von einem Künstler, Band 1). Stuttgart/Berlin: Cotta (reprint Vienna: Universal Edition 1978).
–––. 1935. Der freie Satz (Neue musikalische Theorien und Phantasien, Band 3). Vienna: Universal Edition.
Scherer, Klaus R. 1991. “Emotion Expression in Speech and Music.” In Music, Language, Speech and Brain. Edited by Johan Sundberg, Lennart Nord, and Rolf Carlson. London: Macmillan: 146–56.
Scherer, Klaus R., Rainer Banse, and Harald G. Wallbott. 2001. “Emotion Inferences from Vocal Expression Correlate across Languages and Cultures.” Journal of Cross-Cultural Psychology, 32.1: 76–92.
Scherer, Klaus R., and James S. Oshinsky. 1977. “Cue Utilization in Emotion Attribution from Auditory Stimuli.” Motivation and Emotion 1: 336–46.
Schönberg, Arnold. 1967. Fundamentals of Musical Composition, London: Faber and Faber.
Selincourt, Basil de. 1920. “Music and Duration.” Music and Letters 1, 286–93; In Reflections on Art. Edited by Susanne K. Langer. Oxford: Oxford University Press 1958, 152–60.
Sharpe, Robert A. 1983. “Two Forms of Unity in Music.” The Music Review 44: 274–86.
Shepard, Roger N. 1982. “Structural Representations of Musical Pitch.” In The Psychology of Music. Edited by D. Deutsch. New York: Academic Press, 344–90.
Simon, Herbert A., and Richard K. Sumner. 1968. “Pattern in Music.” In Formal Representation of Human Judgement. Edited by Benjamin Kleinmuntz. New York: John Wiley and Sons, 219–50.
Smith, Karen C., and Lola L. Cuddy. 1986. “The Pleasingness of Melodic Sequences: Contrasting Effects of Repetition and Rule Familiarity.” Psychology of Music 14: 17–32.
Snyder, Bob. 2000. Music and Memory. Cambridge, Massachusetts: MIT Press.
Sparshott, Francis. 1994. “Music and Feeling.” Journal of Aesthetics and Art Criticism 52.1: 23–35.
Spender, Natasha. 1983. “The Cognitive Psychology of Music.” In Psychology Survey No. 4. Edited by John Nicholson and Brian M. Foss. Leicester: British Psychological Society, 266–301.
Teitelbaum, Richard. 1965. “Intervallic Relations in Atonal Music.” Journal of Music Theory 9: 72–127.
Tyson, Alan. 1987. Mozart: Studies of the Autograph Scores. Cambridge, Massachusetts: Harvard University Press.
Thompson, William F., and Brent Robitaille. 1992. “Can Composers Express Emotions Through Music?”Empirical Studies of the Arts, 10: 79–89.
Trehub, Sandra E., and Takayuki Nakata. 2001–2. “Emotion and Music in Infancy.” Musicae Scientiae, Special Issue: Current Trends in the Study of Music and Emotion: 37–61.
Walsh, Stephen. 1984. “Musical Analysis: Hearing is Believing?” Music Perception 2: 237–44.
Watson, Karl B. 1942. “The Nature and Measurement of Musical Meanings.” Psychological Monographs, 54: 1–43.
Zbikowski, Lawrence. 1998. “Metaphor and Music Theory: Reflections from Cognitive Science.” Music Theory Online 4.1.
–––. 2002. Conceptualizing Music: Cognitive Structure, Theory, and Analysis. New York: Oxford University Press.
Dieser Text erscheint im Open Access und ist lizenziert unter einer Creative Commons Namensnennung 4.0 International Lizenz.
This is an open access article licensed under a Creative Commons Attribution 4.0 International License.

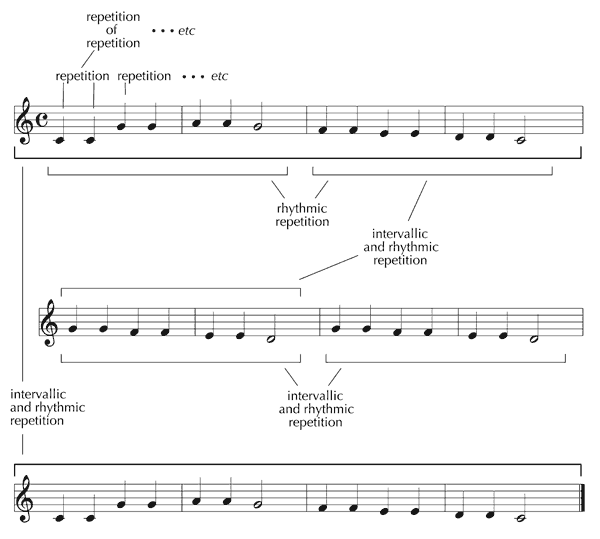
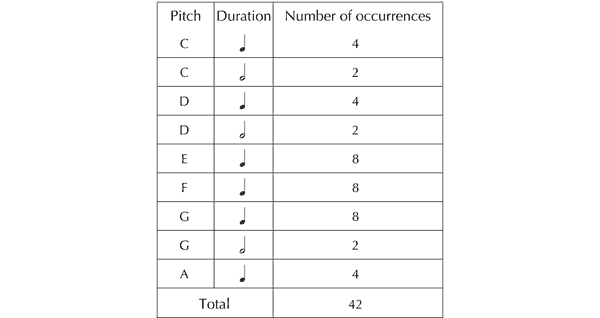
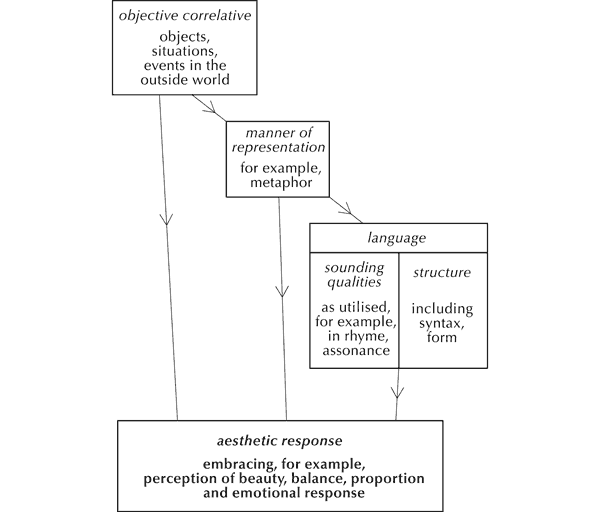
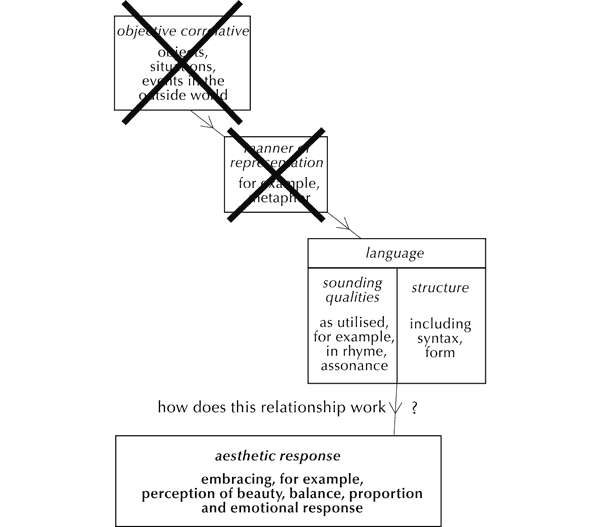
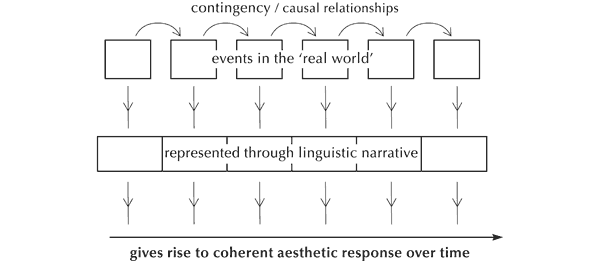
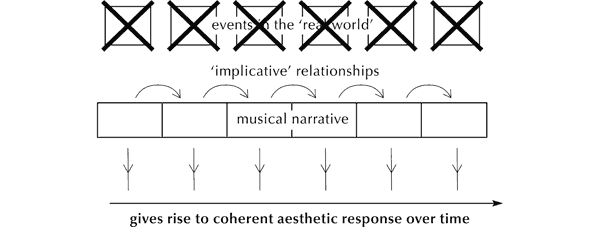


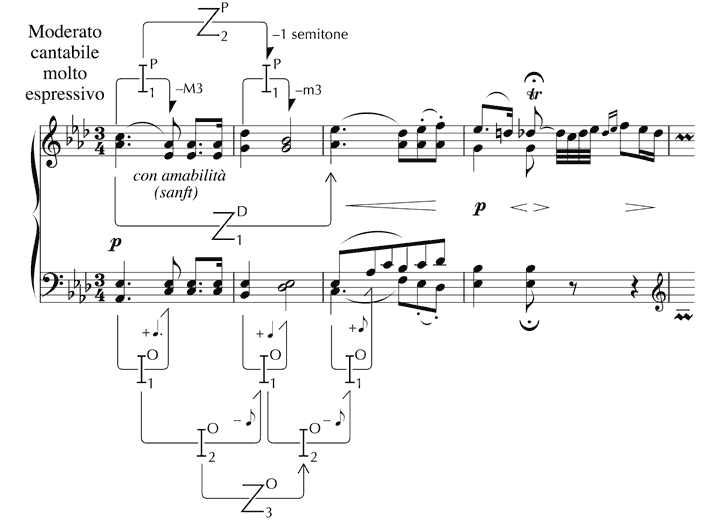
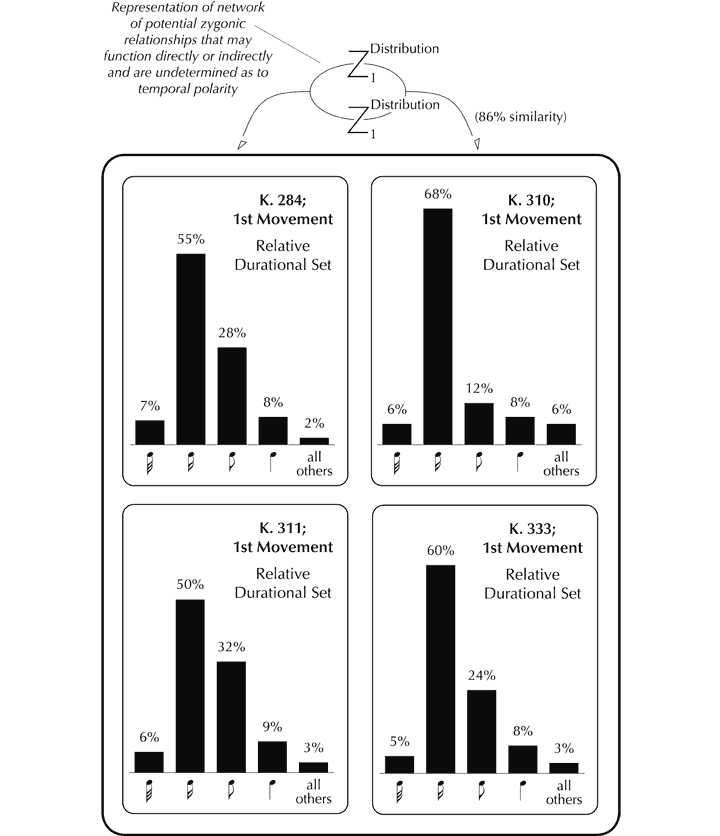
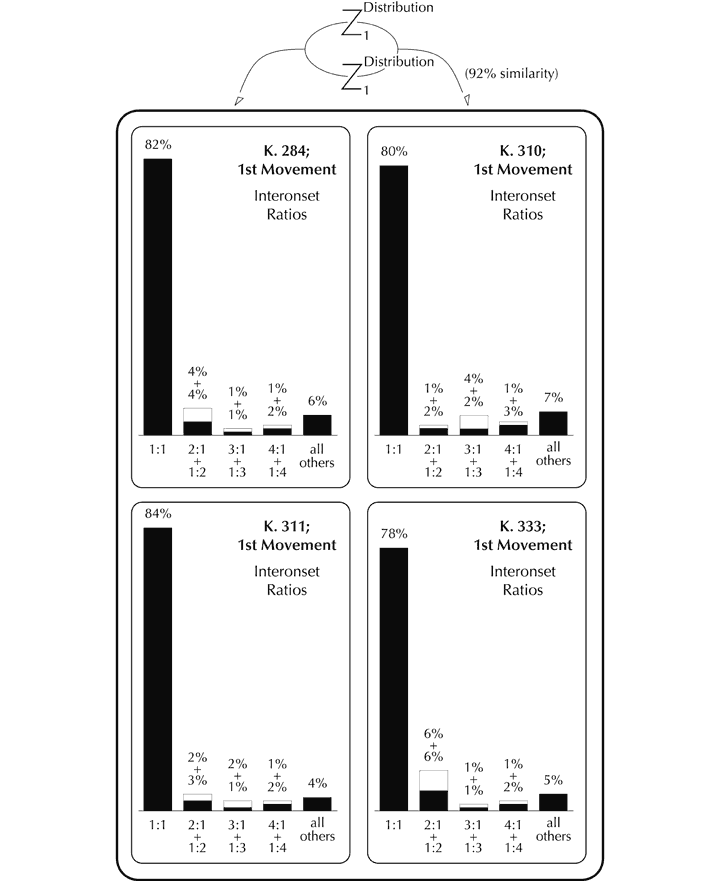
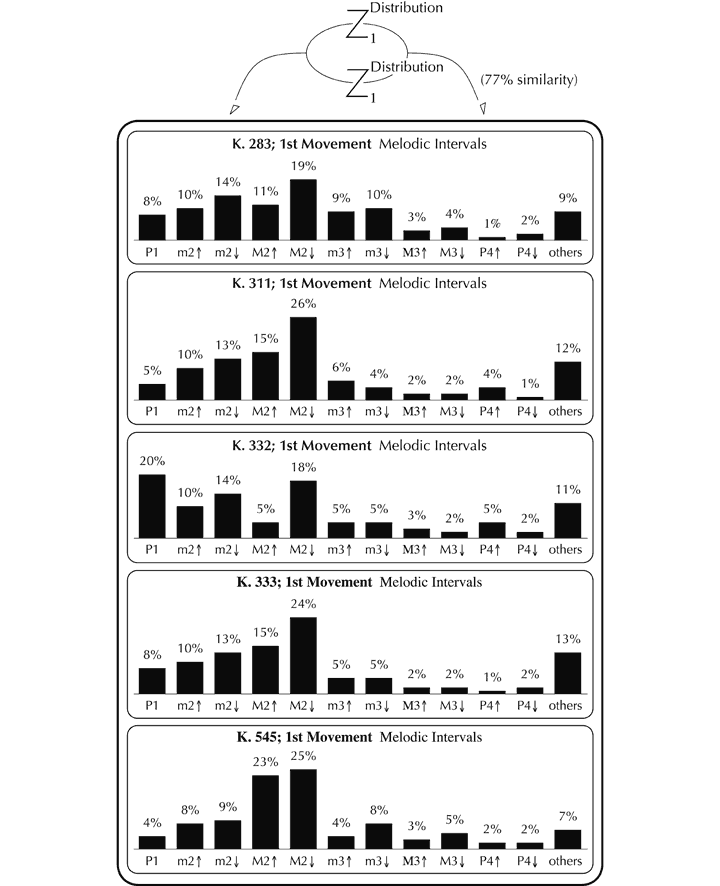
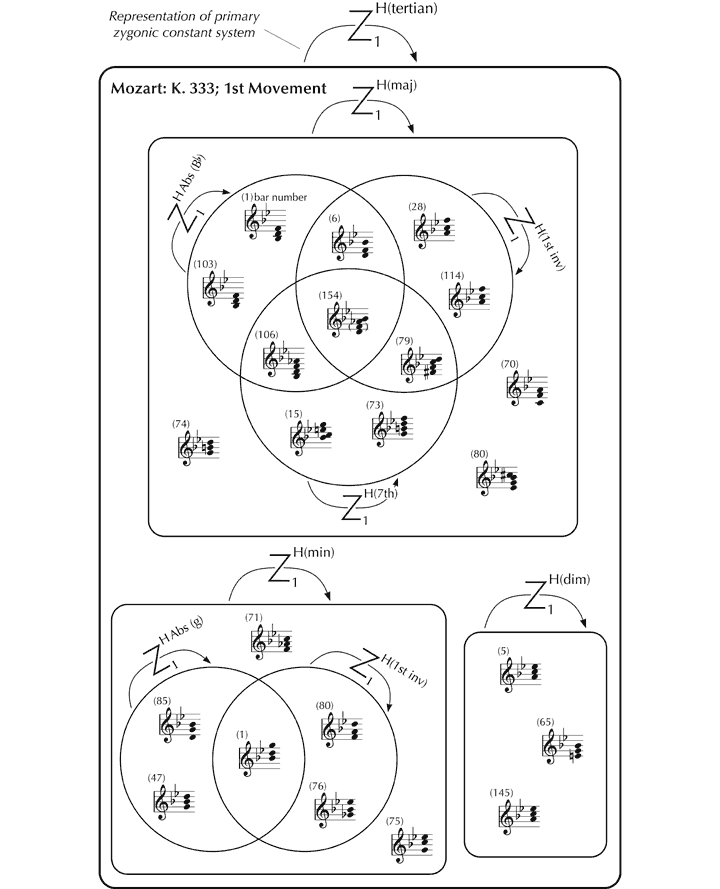
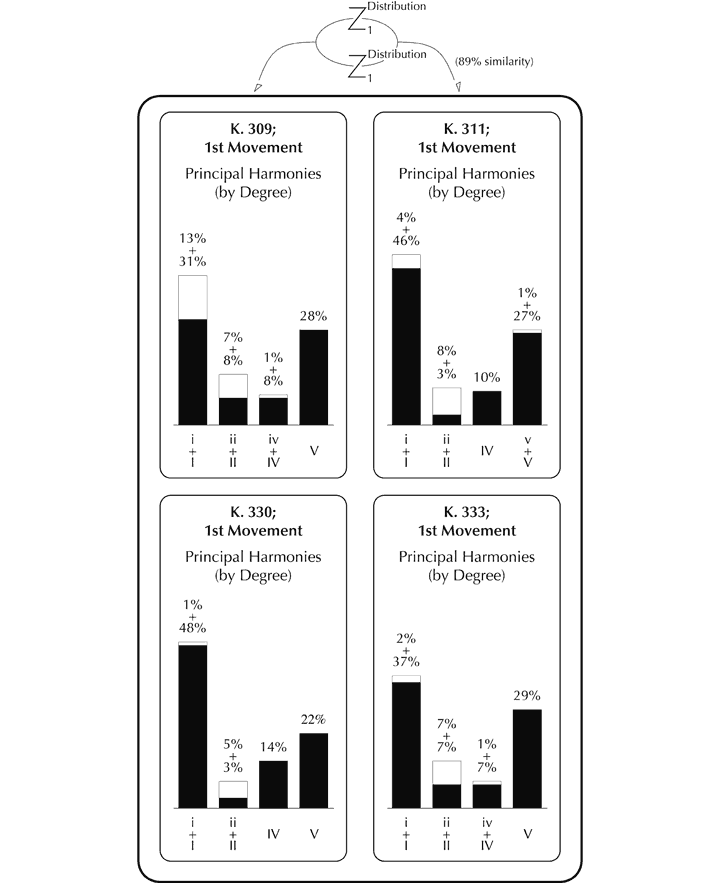
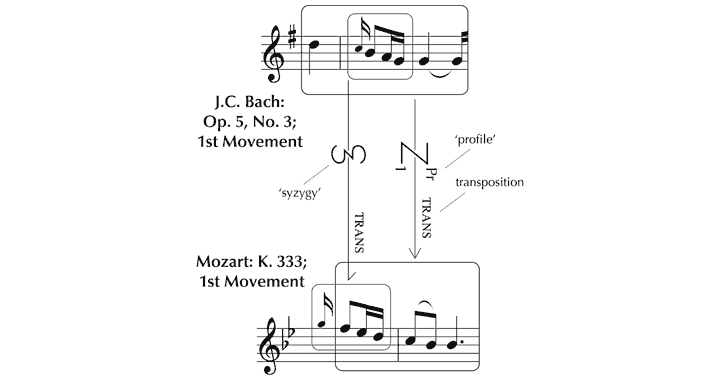
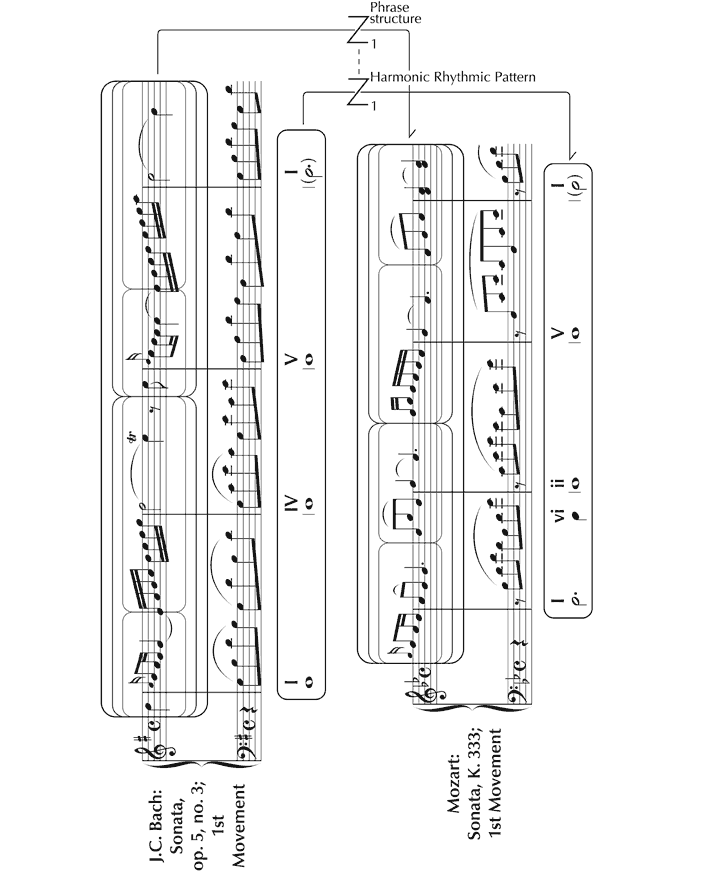
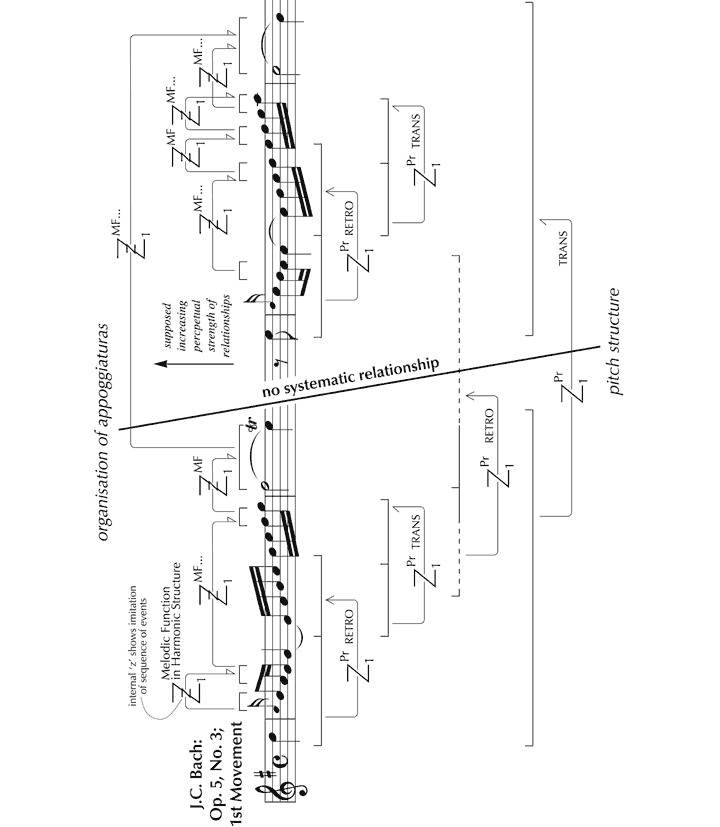
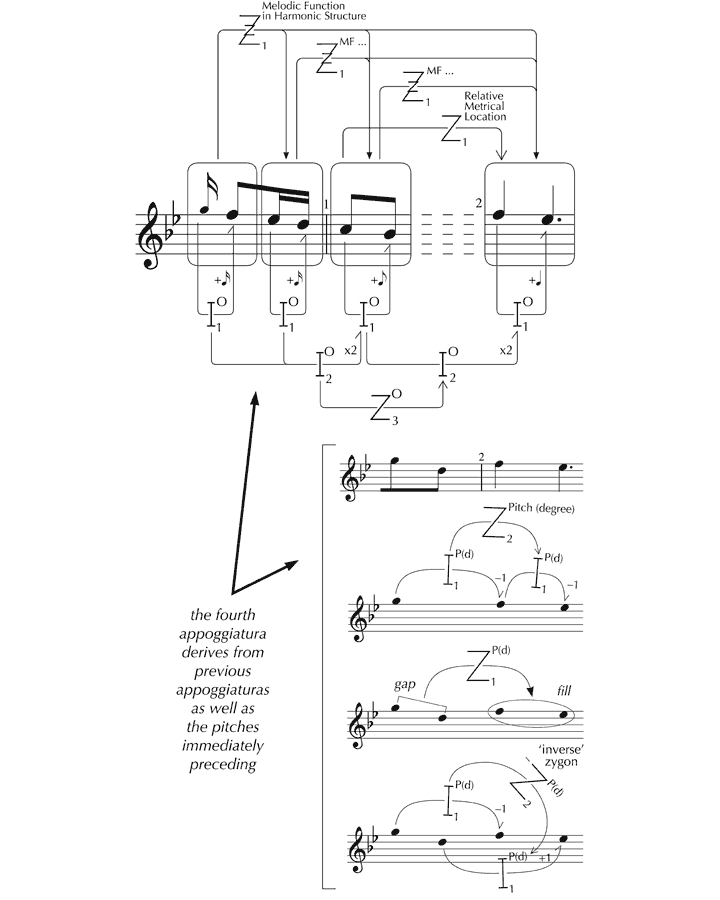
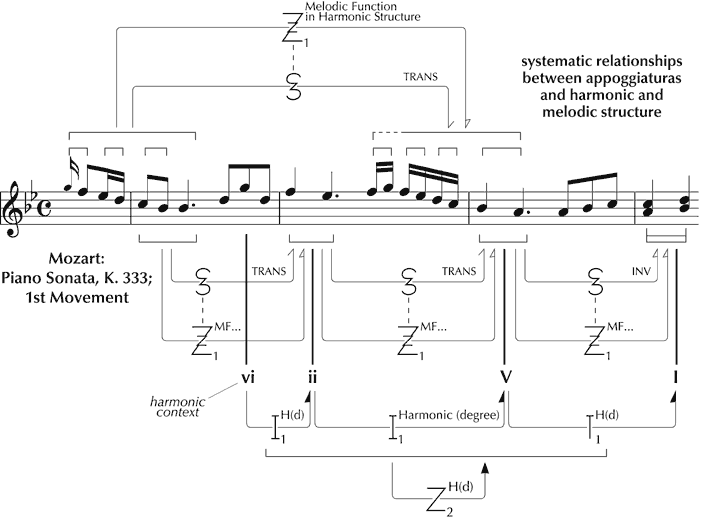
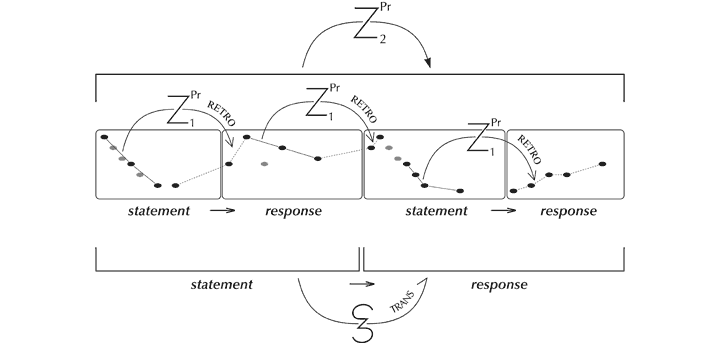




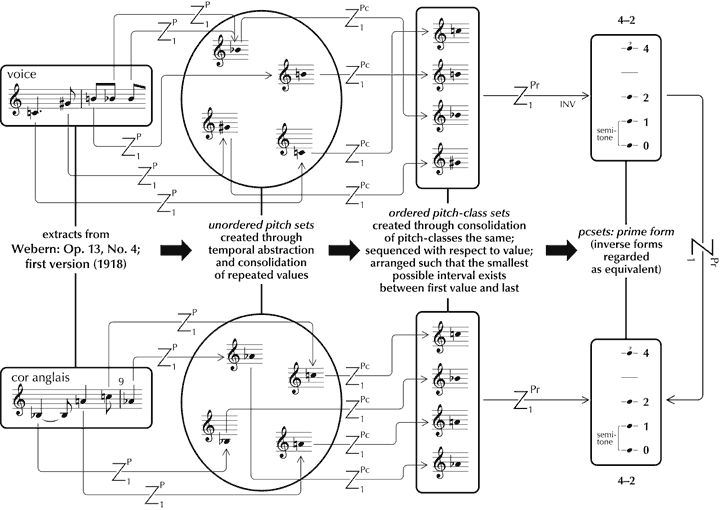

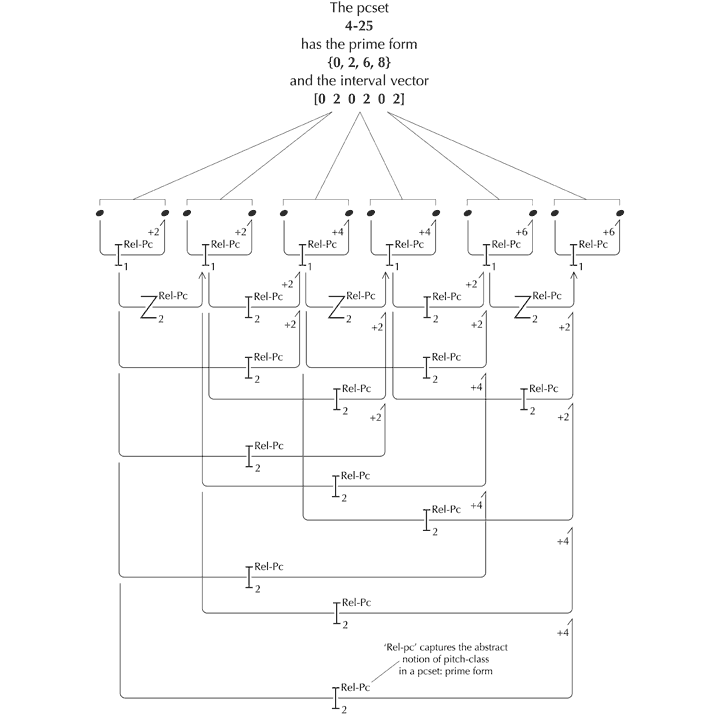
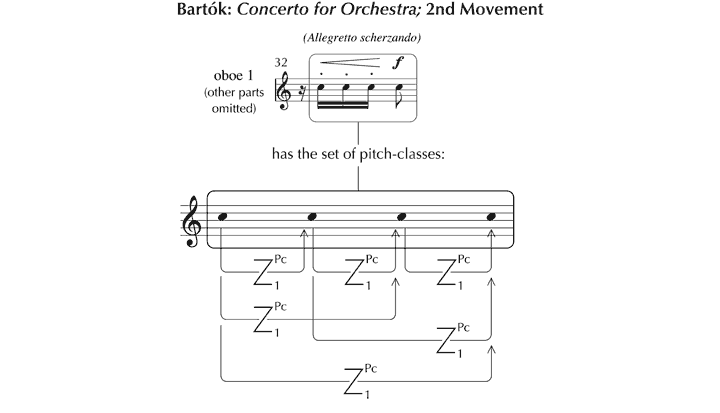
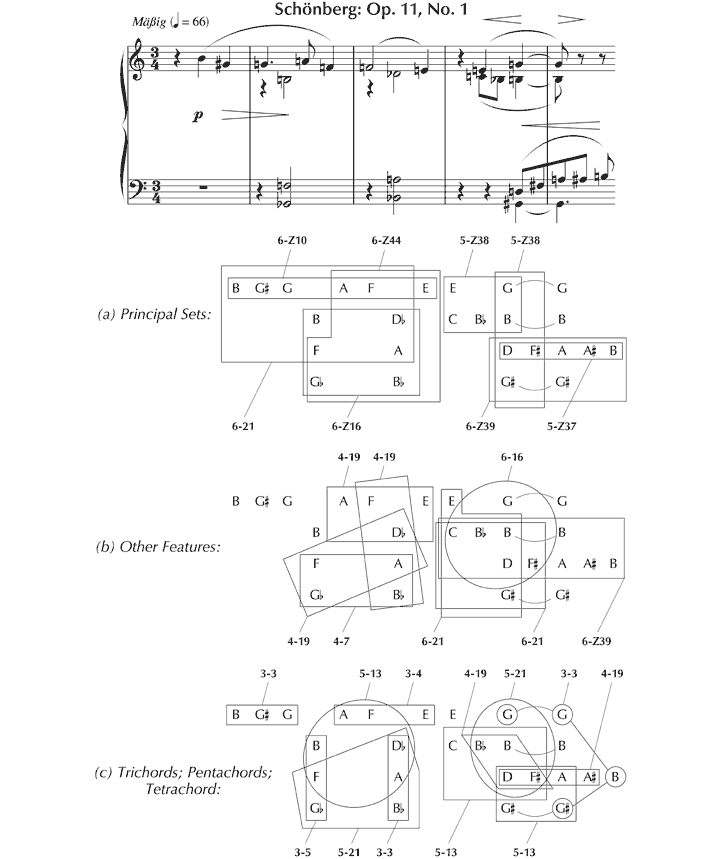
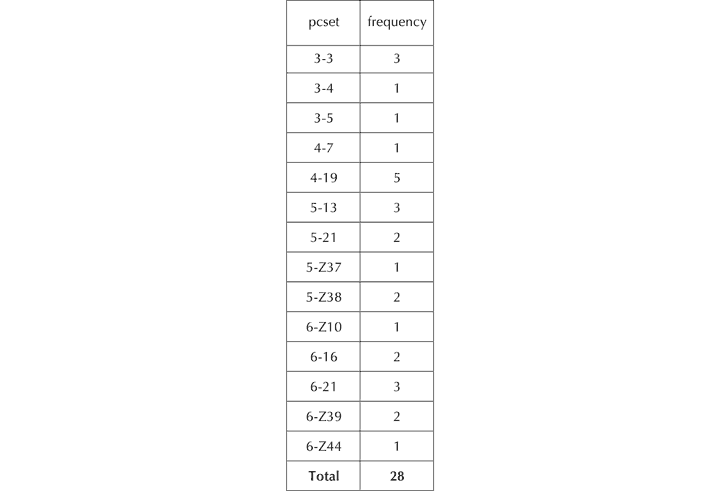
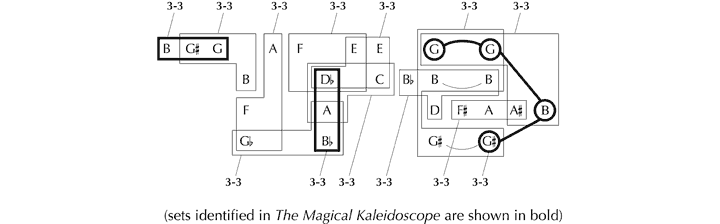
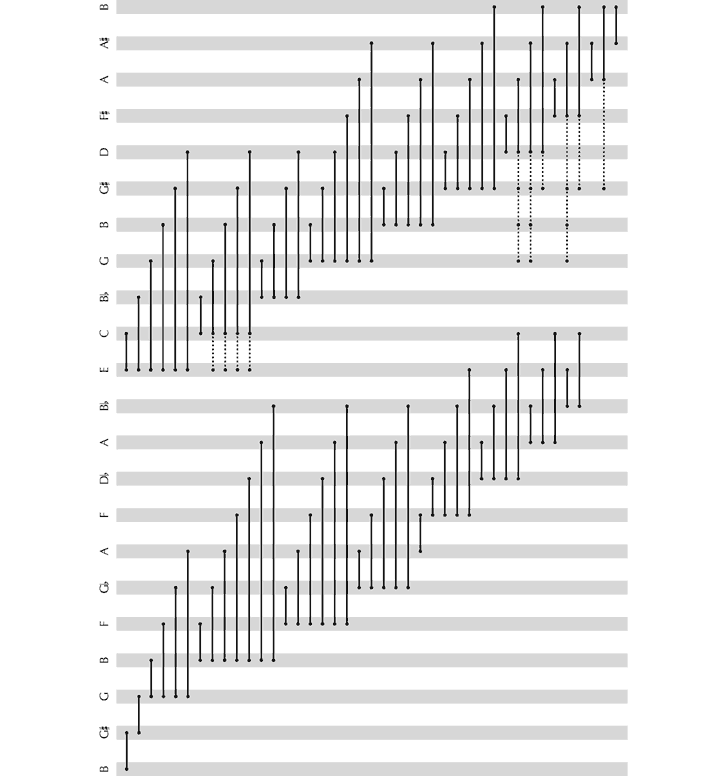
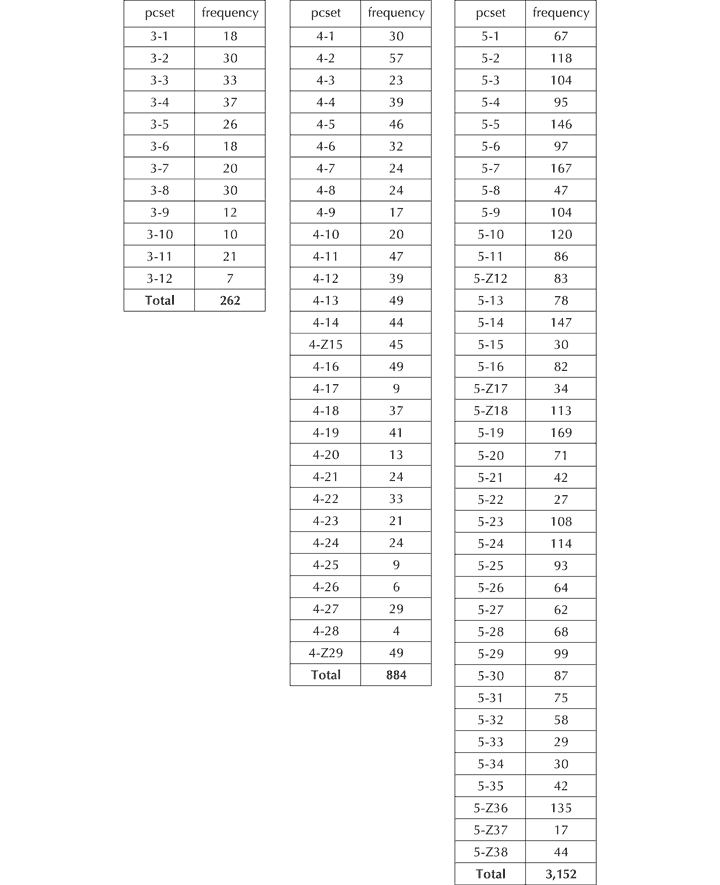
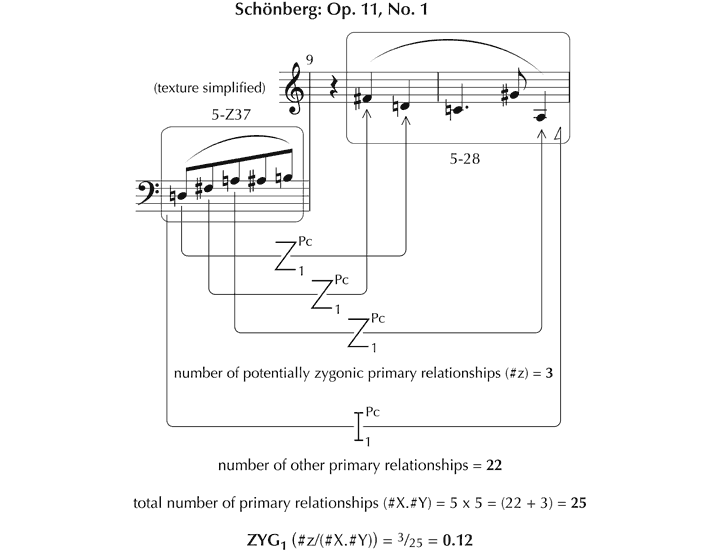
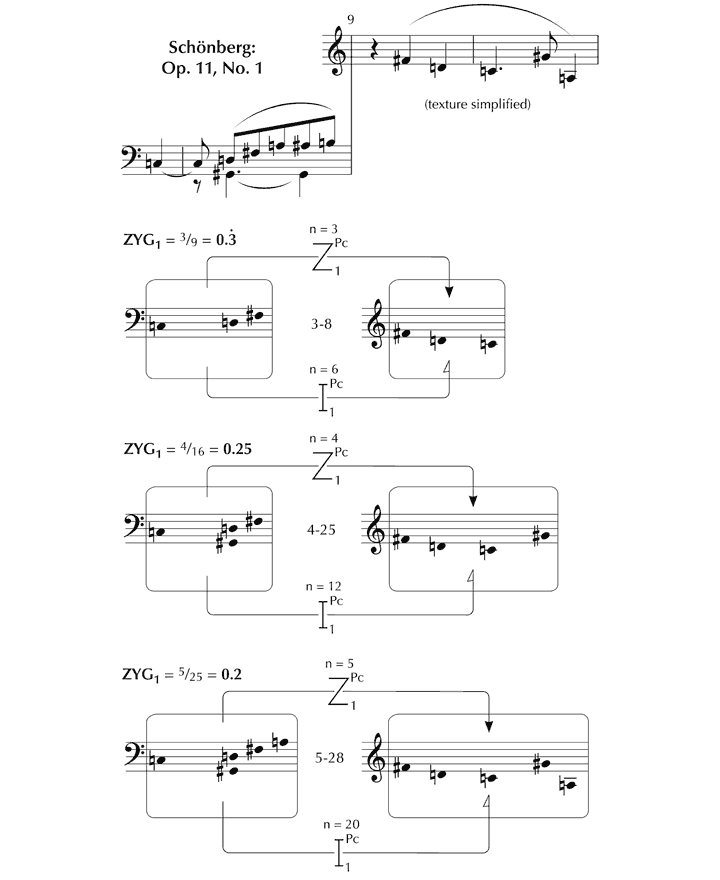

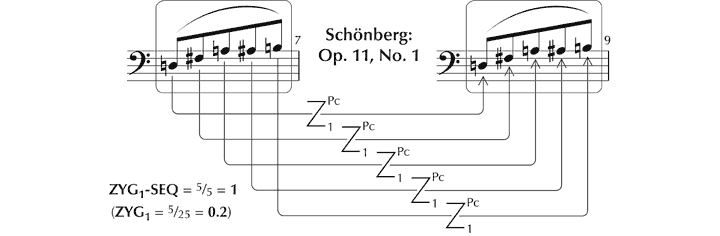
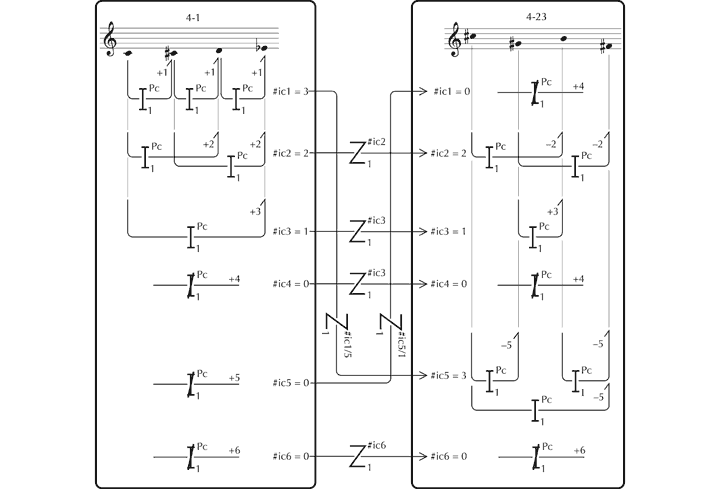
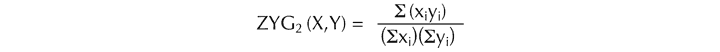
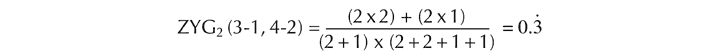
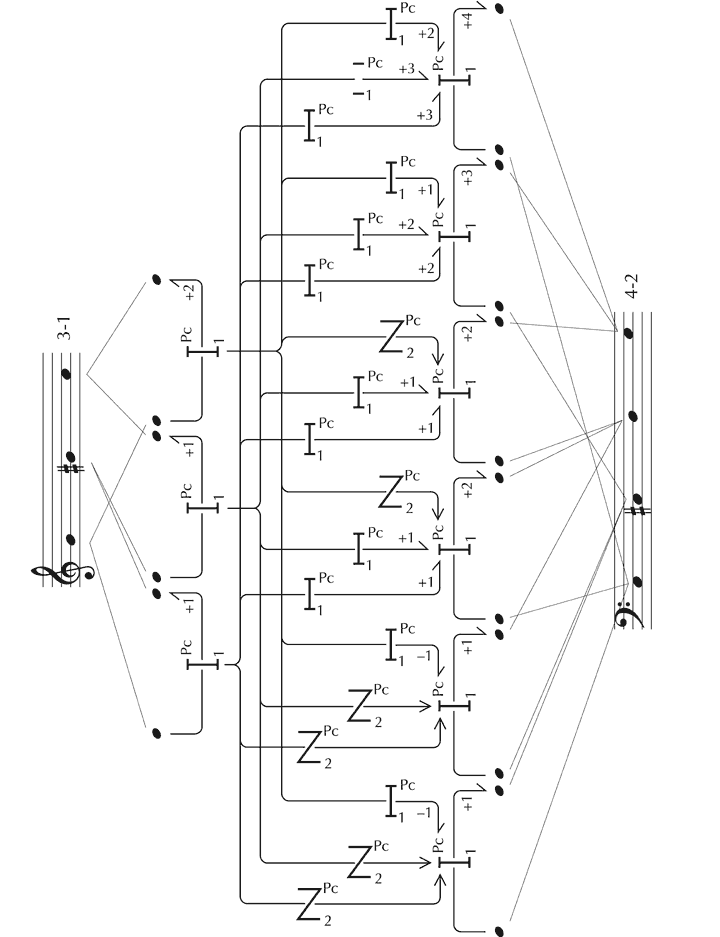
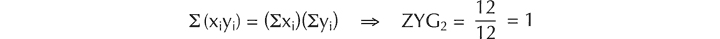

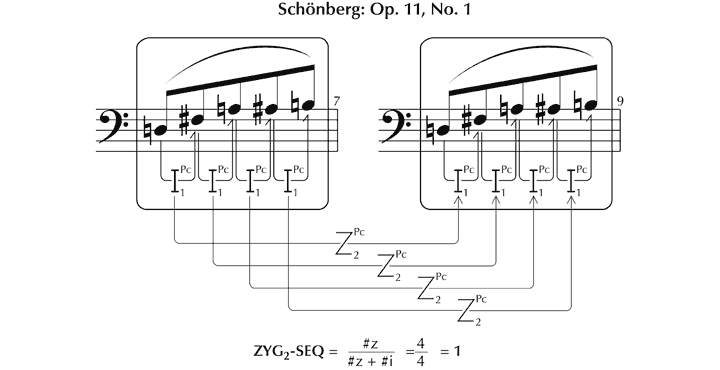



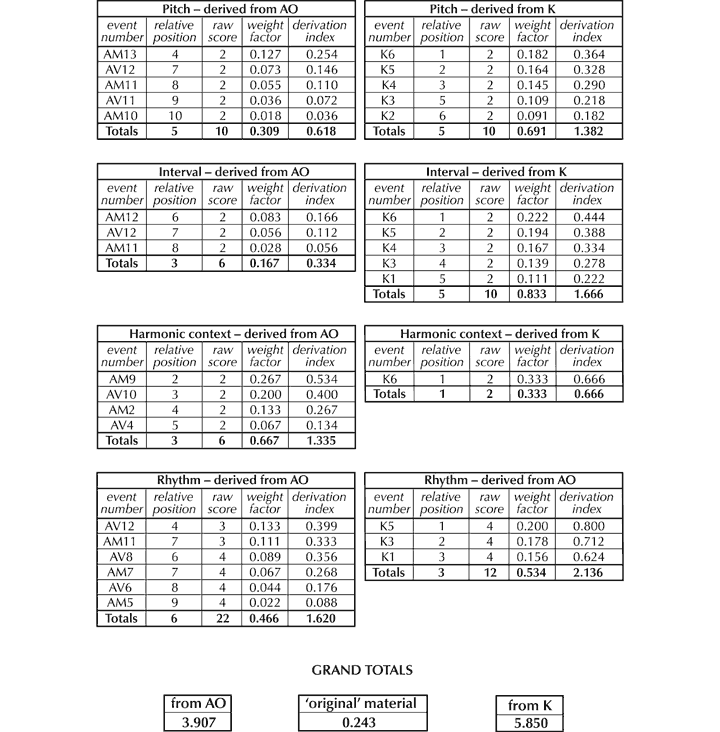

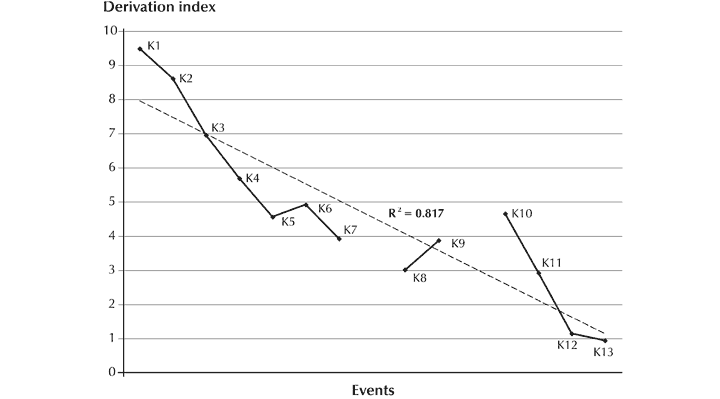
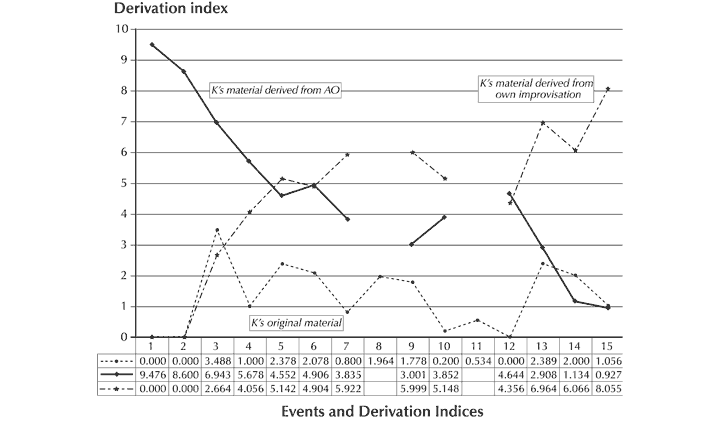
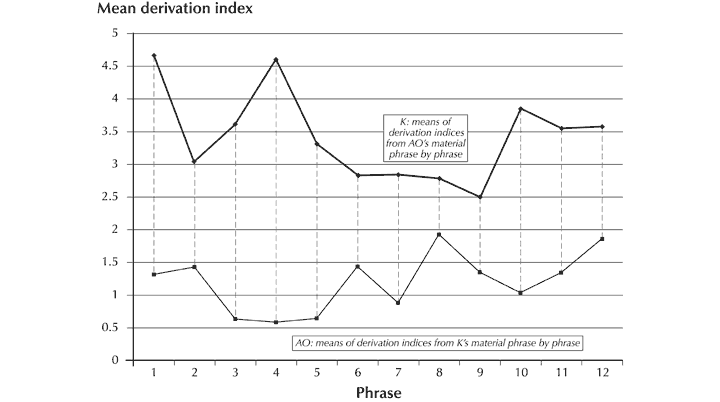
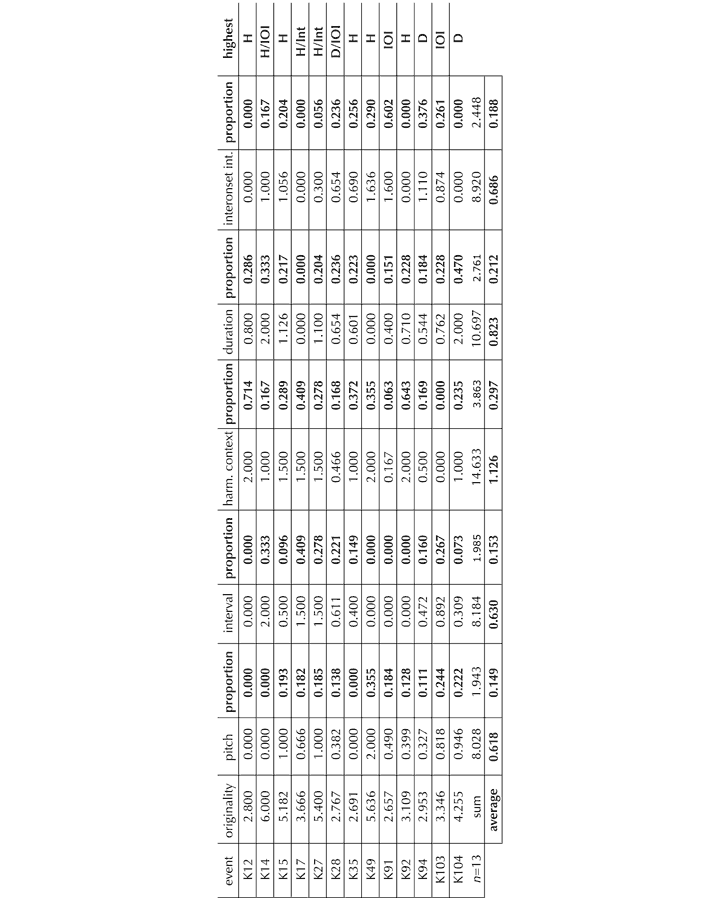
 = 126; Peter Katin (1989)
= 126; Peter Katin (1989)  = 128; Christoph Eschenbach (1971)
= 128; Christoph Eschenbach (1971)  = 129; Paul Badura-Skoda (1989)
= 129; Paul Badura-Skoda (1989)  = 131; Karl Richter (1966)
= 131; Karl Richter (1966)  = 132; Mitsuko Uchida (1984)
= 132; Mitsuko Uchida (1984)  = 132; Andreas Haefliger (1991)
= 132; Andreas Haefliger (1991)  = 132.
= 132. to
to  where
where  = 123; in K. 332 within the range
= 123; in K. 332 within the range  to
to  where
where  = 142; and in K. 576 within the range
= 142; and in K. 576 within the range  to
to  where
where  = 88.
= 88.