Einleitung[2]

Noch vor wenigen Jahrzehnten war es nahezu ausgeschlossen, in einer Zeitschrift oder auf einer Tagung für Musiktheorie afrikanische Musikformen behandelt zu finden. Umgekehrt waren Fachvertreter*innen der Musikethnologie – der damals für ›Außereuropäisches‹ zuständigen Subdisziplin – an einem Austausch kaum interessiert. Im Gegenteil, Konzepte der europäischen Musiktheorie galten als hinderlich für das Verstehen afrikanischer Musiksysteme.[3] In jüngerer Zeit legen beide Seiten vor allem im englischen Sprachraum mehr Wert auf Austausch, doch definiert sich die Musikethnologie mehrheitlich nicht mehr über die geographische Verortung der Untersuchungsgegenstände, sondern über ethnographische Methoden und kulturwissenschaftliche Perspektiven.[4] Da aber die Musiktheorie sich nur zögerlich den Musikformen öffnet, die ehemals der Musikethnologie zugeordnet waren, ist die Perspektive kultureller Diversität in der musikanalytischen und -theoretischen Forschung in Gefahr, fachlich zu verwaisen. In diese Lücke stoßen seit einigen Jahren interdisziplinäre Initiativen, etwa die Bewegung Analytical Approaches to World Music.[5]

Ein Verwaisen der Diversitäts-Perspektive äußerte sich in den vergangenen Jahrzehnten unter anderem darin, dass neue empirische Methoden nach ihrer Einführung einseitig auf euro-amerikanische Musikformen angewandt wurden. So ist etwa die computergestützte Chronometrie von Audio- und MIDI-Aufnahmen seit den 1980er Jahren regelrecht explodiert und hat unser Verständnis von Timing-Strategien, beispielsweise Rubato in europäischer Kunstmusik und Swing-Feel in amerikanischem Jazz, enorm bereichert.[6] Dagegen lassen sich die Timing-Studien afrikanischer Aufführungsstile buchstäblich an einer Hand abzählen.[7] Ein weiteres Beispiel ist die aktuell florierende Analyse umfangreicher Korpora notierter Musik; auch in diesem Bereich liegt der Schwerpunkt noch auf euro-amerikanischen Musikformen.[8] Die rapide Entwicklung digitaler Musikarchive und computergestützter Methoden der Datenextraktion und -analyse laden jedoch zu einer audiobasierten Gegenbewegung ein, die auch schon in Gang gesetzt ist.[9]

Das hier vorgestellte Projekt möchte zu punktuellen Korrekturen eines nach wie vor problematischen eurozentrischen Bias in Teilbereichen der Rhythmusforschung beitragen. Unser Ansatz setzt auf das interdisziplinäre Zusammenspiel von Wissensbeständen und Methoden der Musikethnologie, Musiktheorie, Musikpsychologie und Musikinformatik. Wir analysieren einen Korpus von Audio-Aufnahmen aus Mali und behandeln dabei das Verhältnis von Rhythmus und Metrum (Studie 1), den Status ungleichmäßiger Grundschlagsunterteilung (Studie 2) und die Interaktion musikalischer Rollen bei der Ensemble-Synchronisation (Studie 3).

Korpus

Wir untersuchen einen Korpus live eingespielter Studioaufnahmen von Djembe-Musik aus Bamako (Mali).[10] Die Djembe (jenbe, jembe, djembé) ist eine becherförmige Handtrommel aus Mali und Guinea. Djembe-Spieler[11] waren historisch vor allem zur Tanzbegleitung im Rahmen lokaler Festlichkeiten gefragt. Heute behaupten sie sich auch als Tanztheater-, Konzert- und Studiomusiker sowie in Europa auch als Dozenten für westafrikanische Perkussion.[12]

In Mali sind verschiedene Ensemble-Besetzungen gebräuchlich, etwa das Duo aus einer Djembe und einer zylindrischen Begleittrommel namens Dundun, das Trio aus zwei Djemben und einer Dundun sowie das Quartett aus zwei Djemben und zwei Dunduns. Jedem Spieler ist eine von drei musikalischen Rollen zugewiesen. Die melo-rhythmisch variationsreiche Hauptstimme der ersten Djembe leitet das Ensemble und improvisiert die musikalische Form, sorgt mit virtuoser Ornamentik für Expressivität und koordiniert die Interaktion mit Tanz, Gesang und Publikum. Die erste Dundun spielt eine eingängige, oft asymmetrisch strukturierte Timeline-Figur, deren meist zyklisch-repetitiver Vortrag allen Beteiligten – Ensemble, Tänzer*innen, Sänger*innen und Publikum – zeitliche Orientierung bietet.[13] Die zweite Djembe und zweite Dundun spielen ostinate Begleitfiguren. Sie verdichten das Gewebe des Ensemble-Polyrhythmus und verschaffen damit der ersten Djembe und teilweise auch der ersten Dundun größere Spielräume für Variationsbildung.[14]

Unser Korpus umfasst je vier bis sechs Aufnahmen dreier Stücke des Kernrepertoires der Djembe-Festmusik aus Bamako: Manjanin, Woloso und Maraka. Vier verschiedene Spieler wechseln sich in der Rolle der ersten Djembe ab (Tab. 1). Alle beteiligten Interpreten sind erfahrene urbane Berufstrommler.

Tabelle 1: Zusammensetzung des Korpus

Wir folgen Autor*innen, die eine Anwendung des Metrumsbegriffs in der afrikanistischen Musikforschung befürworten[15], betonen jedoch gleichzeitig die Notwendigkeit, die theoretische Bestimmung des Konzepts ›Metrum‹ offen zu halten. Die Rhythmen der drei Stücke sind vom selben metrischen Typ, einem Zyklus aus vier Grundschlägen (Beat) mit ternärer Unterteilung (Subdivision). Unsere Annahme dieses metrischen Typs beruht auf teilnehmender Beobachtung und musikalischen Analysen und ist konsistent mit dem unten (Studie 2) präsentierten Befund ternärer Timing-Patterns. Sie entspricht darüber hinaus einer etablierten Sichtweise vergleichbarer Polyrhythmen in der westafrikanischen Musikforschung.[16]

Die Audiobeispiele 1a, 1b und 1c stellen Auszüge aus Aufnahmen des Korpus vor. Filmaufnahmen und Analysen der betreffenden Einspielungen sind im Internet abrufbar.[17] Die Abbildungen 1a, 1b und 1c notieren eine typische Phrase je Audiobeispiel. Wir verwenden eine Form der graphischen Rasternotation, wie sie in Teilen der afrikanistischen Rhythmusforschung üblich ist, markieren jedoch nicht nur die Subdivision, sondern auch den Beat. Wir stimmen darin mit der metrischen Auffassung jener Autor*innen überein, die denselben metrischen Typ in europäischer Notenschrift als 12/8 transkribieren und den Wert der punktierten Viertelnote als Grundschlag ansetzen.[18]

Audiobeispiel 1a: Ausschnitt (1:15 min) aus der Aufnahme Manjanin-1 (Drissa Kone Quartett; vgl. Tab. 1). Im Stereobild von links nach rechts: Dundun 1, Djembe 1, Djembe 2 und Dundun 2. Das Exzerpt beginnt mit mehreren Wiederholungen und Variationen der in Abbildung 1a notierten Phrase (knapp 20 Sekunden) und bringt dann weitere Phrasen. Das Tempo steigert sich im Verlauf des Ausschnitts von ca. 155 bpm auf 175 bpm. Zur Erleichterung der metrischen Orientierung beginnt der Ausschnitt mit artifiziell eingefügtem Klatschen auf dem Grundschlag (Beat). Nach drei Zyklen je vier Beats wird das Klatschen wieder ausgeblendet. Wir versuchen lokale Spiel- und Hörweisen insofern nachzubilden, als die Timeline (Dundun 1) nicht mit Beginn des nächsten metrischen 4-Beat-Zyklus (auf dem fünften markierten Beat) einsetzt, sondern entsprechend ihrer figuralen Gestalt mit dem Schlag auf der dritten Subdivision des dritten Beat
(vgl. auch das entsprechende Video unter https://tinyurl.com/Polak-Video-Manjanin). Aufnahme: Polak, Bamako 2006.

Audiobeispiel 1b: Ausschnitt (1:15 min) aus der Aufnahme Woloso-5 (Jeli Madi Kuyate Trio; vgl. Tab. 1). Im Stereobild von links nach rechts: Dundun 1, Djembe 1 und Djembe 2. Das Exzerpt setzt am Beginn der Aufnahme ein und markiert bald darauf mittels artifiziell hinzugefügtem Klatschen einen metrischen 8-Beat-Zyklus und den ersten Beat des folgenden Zyklus (insgesamt neun Beats). Die beiden 8-Beat-Zyklen, die dem mit Klatschen markierten Zyklus unmittelbar folgen, bringen jeweils die in Abbildung 1b notierten Phrasen. Das Tempo beschleunigt von ca. 115 bpm bis auf 145 bpm. Vergleiche das entsprechende Video unter
https://tinyurl.com/Polak-Video-Woloso. Aufnahme: Polak, Bamako 2006.

Audiobeispiel 1c: Ausschnitt (1:15 min) aus der Aufnahme Maraka-2 (Drissa Kone Trio; vgl. Tab. 1). Im Stereobild von links nach rechts: Dundun 1, Djembe 1 und Djembe 2. Das Exzerpt stellt dem Beginn der Aufnahme einen mit Klatschen markieren 4-Beat-Zyklus voran. Die in Abbildung 1c notierte Phrase bzw. Variation davon prägen die ersten 25 Sekunden der Einspielung. Das Tempo steigt von ca. 110 bpm bis auf 155 bpm. Vergleiche das entsprechende Video unter https://tinyurl.com/Polak-Video-Maraka. Aufnahme: Polak, Bamako 2006.

Abbildung 1a–c: Typische melo-rhythmische Patterns für (a) Manjanin, (b) Woloso und (c) Maraka in metrisch annotierter Rasternotation. Durch verschiedene Anschlagsarten sind der Djembe drei grundlegende Sounds zu entlocken, aus denen Klangfarbenmelodien gebildet werden: B(ass)=tief, T(one)=mittel und S(lap)=hoch/hell; die Dundun ermöglicht zwei Sounds: O(ffen)=tief/dunkel und gestoppt (°)=hoch/hell.

Die Textur der Polyrhythmen, die aus dem Ineinandergreifen der einzelnen Ensemble-Parts entstehen, ist von hoher Dichte. Häufig wird nahezu jeder der zwölf metrisch definierten Zeitpunkte im Zyklus durch einen Anschlag mindestens eines der Instrumente im Ensemble artikuliert (Abb. 1). Alle Aufnahmen weisen ein stark ausgeprägtes, nahezu kontinuierliches Accelerando von etwa 100–140 MM bis 160–200 MM auf. In diesem Tempobereich hat die fast durchgehend präsente ternäre Subdivision Dauern von nur 100–200 Millisekunden. Die Frequenz von fünf bis zehn Schlägen pro Sekunde erzeugt den Eindruck einer dichten und rapiden Rhythmik, auch wenn das Beat-Tempo teilweise noch gemäßigt erscheint.

Die Aufnahmen entstanden in den Jahren 2006 und 2007 im Rahmen nicht-öffentlicher Studio-Sessions. Die Musiker improvisierten ihr Repertoire ohne vorherige Proben oder Absprachen, wie es auch für die Aufführungspraxis auf Festen typisch ist. Clipmikrofone (AKG C-419) am Rand jeder Trommel speisten ein mobiles digitales Vierspur-Studio (Edirol R4). Die einzelnen Spuren (WAVE-Dateien mit 16-bit/48-kHz) zeichneten nur wenig Übersprechung der jeweils benachbarten Instrumente mit auf. Die kurze Distanz zwischen Membran und Mikrophon, der stark gerichtete Mikrofontyp und die Aufnahmesituation im Freien, wo kein Raumhall entsteht, spielten hierbei günstig zusammen (Abb. 2). Die Vermessung der Anschläge bedurfte keiner tontechnischen Bearbeitung des Audio-Materials, z.B. durch Frequenzfilter.

Abbildung 2: Studiosession in Bamako im Mai 2007. Von links nach rechts: Madu Jakite (Dundun), Sedu Balo (erste Djembe) und Drissa Kone (zweite Djembe).

Die Audio-Editoren Soundforge, Wavelab, Cubase und Sonic Visualizer dienten der genauen, teils halb-automatisierten[19], teils manuellen Markierung sämtlicher Anschläge. Wir exportierten die Zeitpunkte der rund 42.000 markierten Anschläge als Text-Dateien in ein Kalkulationsprogramm und von dort zur Aufbereitung und Auswertung in die Software Matlab.

Die Anfänge der metrischen 4-Beat-Zyklen ließen sich durch die absolut ostinate Spielweise der zweiten Djembe oder ersatzweise der Dundun (im Fall von Duetten aus nur einer Djembe und Dundun) zunächst annähernd bestimmen. In einem zweiten Schritt definierten wir den Beginn jedes 4-Beat-Zyklus als den Mittelwert der Anschläge aller Parts, die den vorläufig bestimmten Beat artikulieren. Wir berechneten dann sämtliche Anschläge in Relation zur Dauer des jeweils metrischen Zyklus und konnten so die zeitliche Ausdehnung der metrischen Kategorien in Form von Histogrammen erfassen. In jeder Aufnahme zeigen die Histogramme der Onset-Timings zwölf prägnante Cluster der Verteilung im metrischen Zyklus (Abb. 3). Jedes Cluster ist durch ausgesprochen breite und tiefe Kurventäler von seinen Nachbarn getrennt, sodass die meisten Anschläge zuverlässig einer der zwölf metrischen Kategorien zugeordnet werden konnten.

Wir verwarfen gut 2% der ursprünglich markierten Anschläge durch Trimmen am Anfang und Ende der Stücke. Weitere 2% der Anschläge traten in der Nähe von Clustergrenzen auf, wobei es sich ausschließlich um Ornamente der ersten Djembe handelte (Flams, Rolls), die keine metrische Zuordnung intendieren. Diese ornamentalen Anschläge wurden mittels eines Zeitfensters um die Mittelwerte der Cluster gefiltert. Knapp 40.000 metrisch definierte Anschlagszeitpunkte konstituieren den fertig aufbereiteten Korpus, den wir im Folgenden untersuchen.

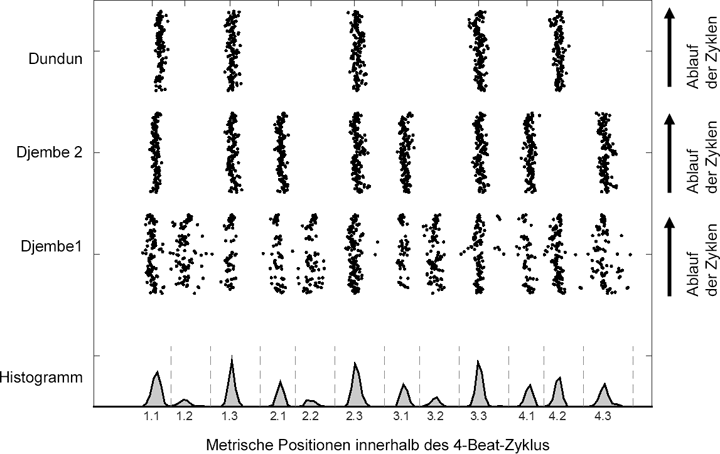
Abbildung 3: Beispiel eines Datensatzes einer Aufnahme von etwa 3:15 Minuten Dauer (Manjanin 3, knapp 3.000 Zeitpunkte). Der obere Bereich zeigt die Daten getrennt nach Ensemble-Parts (Djembe 1, Djembe 2, Dundun). Während die x-Achse die zeitliche Position der aufgetragenen Zeitpunkte innerhalb des metrischen
4-Beat-Zyklus darstellt, zeigt die y-Achse den zeitlichen Verlauf von Zyklus zu Zyklus. Der untere Bereich aggregiert die Datenpunkte sämtlicher Zyklen und Instrumente in einem Histogramm. Die gestrichelten grauen Linien zeigen die Grenzen zwölf diskreter Onset-Cluster, die zwölf metrische Positionen artikulieren.

Studie 1: Metro-rhythmische Gestaltungsweisen

Hintergrund

Viele Rhythmus- bzw. Metrumstheorien verstehen das Verhältnis von Rhythmus und Metrum als eine enge Korrespondenz, die von einer a priori angenommenen Disposition zur Kongruenz her erklärt wird. Das ist offenkundig der Fall bei einer Theorie wie derjenigen Christopher Hastys[20], welche aus rhythmischen Dauern das Potential metrischer Projektionen ableitet. Aber auch jene Theorien, die gruppierend-figurale Rhythmuswahrnehmung und pulsationsbasierte Metrumswahrnehmung unterscheiden, gehen von einer Neigung der Wahrnehmung aus, Rhythmus und Metrum möglichst weitgehend zur Deckung zu bringen.[21] Verschiedene Theorien und Modelle benachbarter Disziplinen teilen diese Annahme, etwa die musikpsychologischen Konzeptionen von Beat-Induktion[22] und dynamischer Aufmerksamkeit[23], Algorithmen zur automatischen Beat- und Tempo-Erkennung[24] und nicht zuletzt auch neurowissenschaftliche Metrumsmodelle[25].

Das folgende, bewusst simple Beispiel soll die Bedeutung dieser Annahme schematisch illustrieren. Man stelle sich eine fortlaufende Reihe perkussiver Anschläge gleicher Klangfarbe und Intensität in moderatem Tempo vor. Alle genannten Theorien gehen davon aus, dass die Wahrnehmung dieses Lautereignisses ein Metrum suggerieren wird, dessen Grundschlag auf der hörbaren Vorgabe synchron aufsetzt. Eine naheliegende Alternative bestünde darin, die klingenden Töne im Offbeat zu hören und somit die Rhythmik und den gefühlten metrischen Grundschlag in ein verzahntes Verhältnis zu setzen. Eine solche gegenphasige Kopplung erschiene ebenso regelmäßig wie die Onbeat-Variante und stellte aus physikalischer Sicht eine durchaus stabile Form der Koordination dar.[26] Sie wird jedoch von keiner der etablierten Metrumstheorien überhaupt erwogen. Hier geht es uns noch nicht darum zu erörtern, ob die Offbeat-Variante beispielsweise für Fans der Stilrichtungen Ska und Reggae eine realistische Hörweise darstellen könnte. Wir wollen zunächst lediglich verdeutlichen, dass die theoretische Eigenständigkeit von Rhythmus und Metrum auch in der anglophonen Musikforschung weniger weit reicht, als deren konzeptuelle Unterscheidung von Gruppierung und Metrum bzw. phänomenalem versus metrischem Akzent vordergründig nahezulegen scheint.[27] Tatsächlich wird der metrischen Struktur zwar oftmals ein gewisses Beharrungsvermögen gegenüber ›abweichenden‹ rhythmischen Akzenten zugetraut, aber kaum Eigenständigkeit.

Für die empirische Untersuchung dieser Thematik kommt eine sehr einfache Form der statistischen Korpusanalyse in Frage, nämlich das schlichte Abzählen der Häufigkeit rhythmischer Ereignisse im Rahmen bestimmter Metren. Mehrere solcher Studien zeigten, dass in europäischen Kunst- und Volksmusikformen die rhythmische Ereignishäufigkeit und metrische Akzentstärke tatsächlich eng korrelieren.[28] Eine graduelle Abweichung besteht beispielsweise im 4/4-Takt darin, dass der Wert für den vierten an denjenigen des dritten Grundschlags beinahe heranreicht, statt dem des zweiten zu entsprechen (vgl. Abb. 4, Positionen 13 [=Beat 4], 5 [=Beat 2] und 9 [=Beat 3]). Die allgemeine Tendenz ist jedoch, dass die Häufigkeitsverteilung rhythmischer Ereigniseinsätze die metrische Hierarchie annähernd widerspiegelt.

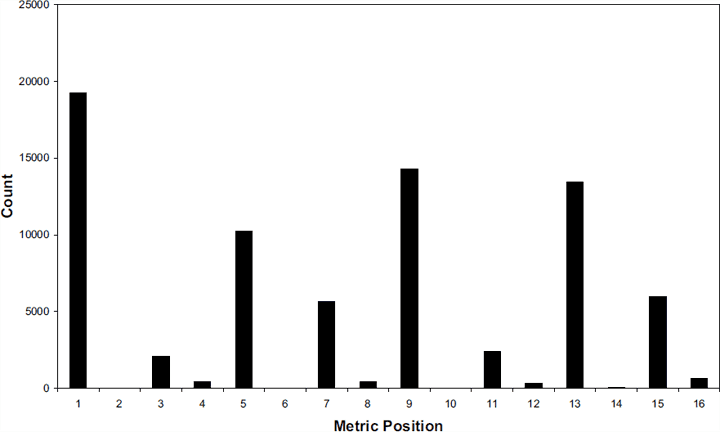
Abbildung 4: Häufigkeitsverteilung der Notenanfänge von gut 1.500 deutschen Volksliedern aus der Essen Folk Song Collection, die im 4/4 Takt stehen.
Die metrischen Positionen 1, 5, 9, und 13 entsprechen den Viertelnoten. (Quelle: Huron/Ommen 2006, Example 4)

André Holzapfel untersuchte das Verhältnis von Eventhäufigkeit und Metrum in einem Korpus von über 900 notierten Stücken modaler türkischer Vokalmusik.[29] In dieser Musikform werden Melodien im Kontext spezifischer rhythmischer Modi (Usul) konzipiert. Grundlegende Schlagfolgen der Trommelbegleitung repräsentieren diese Modi häufig, sind im untersuchten Korpus allerdings nicht notiert. Holzapfel stellte fest, dass die Eventhäufigkeit in der Vokalmusik relativ eng mit den Usul-Patterns korrespondiert (Abb. 5). Das Usul-Konzept prägt die Rhythmik von Melodien also auch in Abwesenheit von Trommelbegleitung. Metrische Hierarchien im Sinne einer Schichtung von Pulsationen verschiedener Dichte treten beispielsweise im Usul Semai zutage (vgl. Abb. 5d), keineswegs aber in allen Modi. So bespielt etwa der 16-schlägige Düyek den zweiten metrischen Grundschlag in Position 5 deutlich seltener als die Positionen 3 und 7 (Abb. 5c). Holzapfel schließt auf eine Rhythmuskonzeption, die zwar eine Metrik ähnlich der europäischen Vorstellung einschließt, aber weniger stark von einer hierarchischen Schichtung metrischer Ebenen geprägt ist.

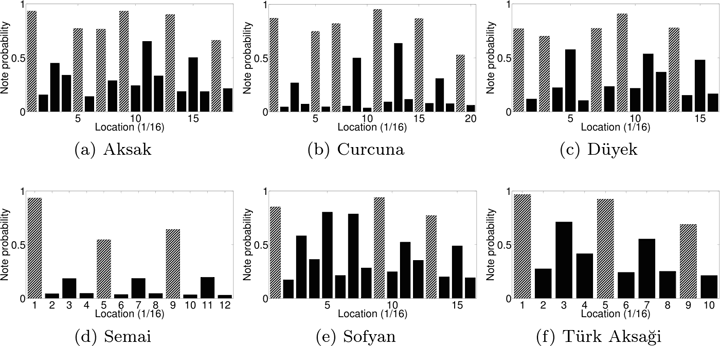
Abbildung 5: Verteilung der Noteneinsatzhäufigkeit in Bezug auf die metrische Position in einem Korpus türkischer Maqam-Musik, getrennt nach rhythmischen Modi (Usul). Die x-Achse zeigt die metrischen Zyklen, die y-Ache die Eventhäufigkeit. Die Balken der Positionen, die den Usul kennzeichnen,
sind grau schraffiert, die anderen schwarz. (Quelle: Holzapfel 2015, Abb. 5)

Der Annahme einer gleichsam natürlichen Tendenz zur Kongruenz im Verhältnis von Rhythmus und Metrum wird oft implizit und teils auch explizit ein universeller Status zugesprochen. Holzapfels Befund erscheint nicht eindeutig konsistent mit dieser Annahme und unterstreicht die Notwendigkeit weiterer Prüfung in kulturvergleichender Perspektive.

Die afrikanistische Rhythmustheorie entwickelte während ihrer Blütezeit, die von den 1950er- bis in die 1980er-Jahre reichte, wahrnehmungsorientierte Metrumskonzeptionen, die teils explizit als Antithese zur europäischen Annahme eines Kongruenzbestrebens formuliert wurden. In einem bahnbrechenden Artikel zum seiner Meinung nach typisch afrikanischen ›Metronomsinn‹ nahm Richard Waterman bereits 1952 zentrale Aspekte der psychologischen Konzepte von Beat-Induktion und Pulsation, dynamischer Aufmerksamkeit und metrischer Expektanz um Jahrzehnte vorweg. Es sind diese Konzepte, deren Konvergenz die Entstehung der pulsationsbasierten nordamerikanischen Metrumstheorie in den 1970er- bis 1990er-Jahren prägten.[30]

From the point of view of the listener, [the metronome sense] entails habits of conceiving any music as structured along a theoretical framework of beats regularly spaced in time […], whether or not the beats are expressed in actual melodic or percussion tones. […]

The maintenance of a subjective meter, in terms of the metronome sense, requires effort and, more particularly, a series of efforts regularly spaced in time. The regular recurrence of these ›rhythmic awarenesses‹ involves the expectancy, at the moment of any beat, that the next beat will occur precisely at some succeeding moment determined by the tempo. Subjectively, the beat does occur. If it is reinforced by an objective stimulus in the form of a percussive or melodic tone, the metronome sense is reassured, and the effort involved in the subjective beat is masked by the effort of perceiving the objective pulse. If the objective beat is omitted, however, the co-operating auditor becomes very much aware of the subjective beat, which thus attains for him greatly increased significance.[31]

In der afrikanistischen Musikethnologie begründete Waterman eine metrumstheoretische Tradition, die Pulsationen als Wahrnehmung periodischer Zeitpunktreihen auf drei Ebenen unterscheidet: Zyklus, Grundschlag und Grundschlagsunterteilung.[32] Dieser Diskurs betonte, dass die Wahrnehmung von Pulsation potentiell von Klangereignissen unabhängig sei und ihr Ablauf aus äquivalenten, nicht gewichteten Zeitpunktswahrnehmungen bestünde. Dies wurde explizit europäischen Metrumskonzepten gegenübergestellt, die Zeitpunktsabläufe als Alternation verschieden gewichteter Akzentstufen begreifen und dabei annehmen, das rhythmisch-metrische Kongruenzbestreben verlange eine rhythmisch-phänomenale Ausprägung entsprechender Akzentstärkemuster: »Im Gegensatz zum Takt in der europäischen Musik enthält der Beat in afrikanischen Musikarten keine Vorstellung von schweren und leichten Taktteilen.«[33] Ganz im Gegenteil wurde angenommen, ›kontrametrische‹ rhythmische Gestaltungsweisen wie Offbeat-Phrasierung und Kreuzrhythmik prägten die afrikanische Rhythmik.[34]

Aus dem zwar uneinheitlich entwickelten Theoriediskurs der afrikanistischen Musikforschung ergibt sich die inhaltlich doch klar konturierte Hypothese, dass Metren in der afrikanischen Musik nicht direkt aus rhythmischen Strukturen abzuleiten sind. Diese Hypothese begründet die Vorhersage, dass die Analyse unseres Korpus malischer Djembe-Musik kein kongruentes Abbild der metrischen Struktur in der Verteilung rhythmischer Eventhäufigkeiten zutage fördern wird.

Methode und Befund

Die Abbildung 6a zeigt für die drei Stücke im Korpus jeweils ähnliche Häufigkeitsverteilungen der rhythmischen Ereignisse (Anschläge) im metrischen Zyklus. Von den vier metrischen Grundschlägen weist nur der erste – der verschiedentlich als ›Downbeat‹ angesprochene Anfangs- und Endpunkt des Zyklus – herausragend hohe Werte auf. Die Beats Nummer 2, 3 und 4 zählen meist weniger Anschläge als die dritte Subdivision des jeweils vorhergehenden Beats. Die zweite Subdivision ist dagegen schwächer besetzt als die dritte. Die von der Dundun-Timeline markierten Positionen weisen relativ hohe Werte auf.

Die getrennte Betrachtung der vier bis sechs Aufnahmen je Stück bringt zwar einzelne Abweichungen ans Licht, etwa vergleichsweise hohe Werte für Beat 4.2 in der Aufnahme Manjanin 2 (Abb. 6b). In keinem Fall führt eine solche Abweichung aber zu einem anderen Gesamtbild, etwa zu einer deutlichen Artikulation des metrischen Grundschlags. Schließlich macht die Gegenüberstellung der ersten und zweiten Hälfte sämtlicher Aufnahmen sichtbar, dass keine Abhängigkeit vom Tempo besteht, das im Verlauf aller Aufnahmen stark ansteigt (Abb. 6c). Die in Abbildung 6a dargestellten Häufigkeitsverteilungen repräsentieren also für jedes Stück spezifische, markante Muster und nicht etwa abstrakte Mittelwerte hochgradig variablen Verhaltens.

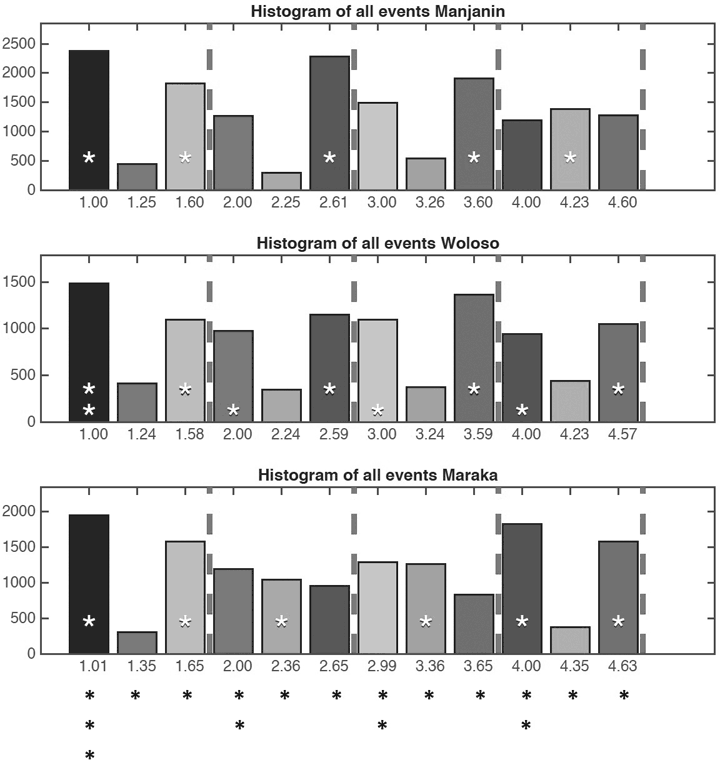
Abbildung 6a: Histogramm der Anschläge in Relation zur metrischen Position, getrennt nach Stücken; die 2–4 Ensembleparts je Aufnahme und 4–6 Aufnahmen je Stück sind aggregiert. Sternchen innerhalb der Balken markieren metrische Positionen, die durch Anschläge der Dundun (Timeline) artikuliert werden; die Timeline im Stück Woloso erstreckt sich über zwei Zyklen und weist dementsprechend zwei Reihen von Sternchen auf. Gestrichelte vertikale Linien markieren die Grenze zwischen den Beat-Spannen. Die hierarchische Struktur des metrischen Typus (vier Grundschläge mit je drei Unterteilungen je Zyklus), der allen drei Stücken unterliegt, ist unterhalb der Histogramme in Form einer Punkte-Grafik dargestellt. (Quelle: London/Polak/Jacoby 2016, Fig. 5)

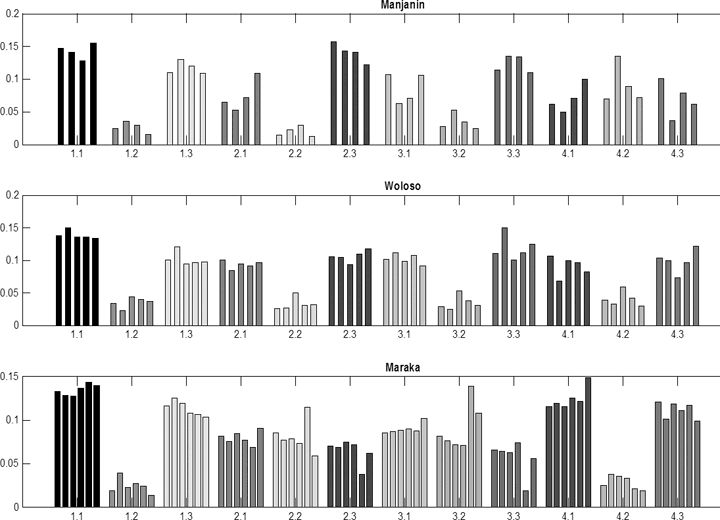
Abbildung 6b: Histogramm der Anschläge in Relation zur metrischen Position, getrennt nach Stücken und Aufnahmen.
Die Balken gleicher Grauschattierung in einer metrischen Position repräsentieren je eine Aufnahme des betreffenden Stücks.

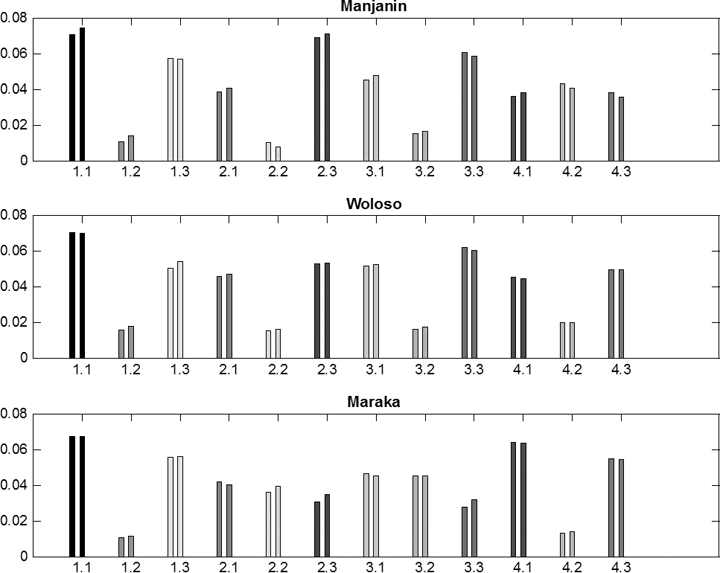
Abbildung 6c: Histogramm der Anschläge in Relation zur metrischen Position, getrennt nach Stücken und erster versus zweiter Hälfte der Aufnahmen
(linker versus rechter Balken gleicher Grauschattierung in jeder metrischen Position)

Diskussion

Die musikethnologische Tendenz, afrikanische und europäische Formen von Rhythmik als völlig unvergleichbar gegenüberzustellen, hat Kritik erfahren.[35] Dies sollte uns jedoch nicht davon abhalten, den oben vorgelegten Befund ernst zu nehmen: Rhythmische Ereignishäufigkeit korreliert in den untersuchten westafrikanischen Musikformen nicht mit metrischer Akzentstärke. Dies schließt keineswegs aus, dass das Verhältnis von Rhythmus und Metrum in der Djembe-Musik als statistische Korrelation höherer Ordnung beschreibbar ist.[36] Der Befund ist jedoch ohne Zweifel inkonsistent mit der für europäische Theorien grundlegenden Annahme, metrische Akzentstärken und -strukturen seien unmittelbar von phänomenalen, insbesondere rhythmischen Akzentmustern abzuleiten. Nach Lerdahl und Jackendoff gilt: »Phenomenal accent functions as a perceptual input to metrical accent—that is, the moments of musical stress in the raw signal serve as ›cues‹ from which the listener attempts to extrapolate a regular pattern of metrical accents«[37]. Für die Djembe-Musik ist dieses Modell der Generierung metrischer Akzentstrukturen offenkundig nicht angemessen. Insbesondere geht hier der metrische Grundschlag (Beat) nicht mit einer entsprechend hohen Ereignishäufigkeit einher. Relevante Einflussfaktoren sind u.a. die Timeline der Dundun, Offbeat-Phrasierung und Kreuzrhythmik der ersten Djembe sowie die Shuffle-Figur der zweiten Djembe. Die vergleichsweise repetitive Rhythmik ergibt jedoch für jedes Stück im Repertoire ein markantes Muster der Häufigkeitsverteilung. Das stabile Verhältnis dieser Muster zum Metrum stellt eine verlässliche Umgebung für Prozesse impliziten Lernens dar, wie sie für Metrumslernen angenommen werden dürfen.[38] Djembe-Rhythmen erklingen als melodische Figuren und erscheinen multi-sensorisch eingebettet in Aufführungskontexte, in denen Teilnehmer*innen auch singen, tanzen, klatschen usw. In ästhetisch, sozial und kulturell derart reichhaltigen Umwelten scheint aktiv-unterrichtende, musikpädagogische Intervention nicht nötig zu sein, um die Periodizität der Beat-Spanne in der komplexen, multimodalen Ereignisstruktur wahrzunehmen und den Beat-Bezug als kulturelles Schema zu erlernen. In Mali findet aktive musikalische Unterweisung jedenfalls kaum statt, und die Bevölkerung hat dennoch keine Probleme damit, öffentliche Tanzveranstaltungen mit metro-rhythmisch inkongruenter, polyrhythmischer Tanzmusik zu bestreiten.

Die vorgelegte Studie liefert einen quantitativen empirischen Beleg für das in der Musikethnologie seit den 1950er-Jahren postulierte und mit den Mitteln konventioneller Analyse vielfach beschriebene Fehlen eines klaren Kongruenzverhältnisses von Rhythmus und Metrum in afrikanischen Musikformen. Dies gibt Anlass, die Loslösung der allgemeinen Metrumstheorie von Festschreibungen durch europäische Repertoires und Theorietraditionen voranzutreiben. Aussichtsreich erscheint der Anschluss an die pulsationsbasierte nordamerikanische Musiktheorie, die mit ihrer Unterscheidung von Rhythmus und Metrum nicht-kongruente metro-rhythmische Verhältnisse potentiell fassbar macht. Allerdings hat sie diesen theoretischen Rahmen mit metrischen Präferenzregeln besetzt, die metro-rhythmische Kongruenz als Idealfall setzt, und lässt damit einen Teil ihrer analytischen Möglichkeiten ungenutzt. Lerdahl und Jackendoffs metrische Präferenzregel 3, der zufolge Ereignishäufigkeit und metrische Akzentuierung korrelieren[39], würde etwa im Stück Manjanin die dritte Subdivision als Grundschlag nahelegen und damit in die Irre führen. Um unseren westafrikanischen Korpus realistisch erfassen zu können, müsste sie folgendermaßen angepasst werden: ›Bevorzuge im Falle ternärer Grundschlagsunterteilung ein Metrum, in dem Ereignisse nicht häufig auf die zweite Subdivision fallen‹. Entsprechend dieser Regel erscheinen Schläge auf der zweiten, aber nicht auch solche auf der dritten Subdivision als Abweichung von einer metrischen Erwartung. Im Unterschied dazu schreibt etwa das Konzept der Synkope[40] allen Offbeats und somit auch der dritten Subdivision metro-rhythmisches Spannungspotential zu. Dieser Unterschied verdeutlicht, dass das Konzept der Synkope auf einer nicht universellen, sondern kulturspezifischen Vorannahme beruht, nämlich der europäisch geprägten Annahme einer Disposition zu kommetrischer Rhythmik bzw. metro-rhythmischer Kongruenz.

Studie 2: Performance-Timing der Grundschlagsunterteilung

Hintergrund und Hypothesen

Fallstudien verschiedener Formen malischer Perkussionsmusik zeigen konsistente Muster ungleichmäßiger Grundschlagsunterteilung und argumentieren für die Hypothese eines metrisch-normativen Status solcher Muster.[41] Die These metrischer Timing-Patterns vertreten auch Studien brasilianischer und skandinavischer Tanzmusikformen.[42] Dementgegen steht die konventionelle Annahme, ungleichmäßige Grundschlagsunterteilungen, wie etwa die Swing-Achtel im Jazz, stellten rhythmische Abweichungen von einer kognitiv gleichmäßigen metrischen Pulsation dar.[43] Auch die afrikanistische Rhythmustheorie vertritt die Auffassung, dass die schnelle Pulsation auf der Ebene der Grundschlagsunterteilung strikt isochron strukturiert ist und etwaige performative Abweichungen ›zurechtgehört‹ werden.[44]

Rhythmische Timing-Variationen können sich auf verschiedene Aspekte der Musikform beziehen. Agogische Phrasierung und freies Rubato betreffen beispielsweise Strukturen der Gruppierung.[45] Aber auch metrische Periodizitäten sind Gegenstand rhythmischer Timing-Variationen, z.B. die Ebene der Viertel-Noten im Wiener Walzer[46] oder die schon angesprochene Swing-Achtel im Jazz. Timing-Variationen können der Erzeugung von Expressivität dienen, im Sinne einer musikalischen Strukturverdeutlichung oder emotionalen Ausdrucksverdeutlichung oder auch im Sinne einer intransitiven Expressivität ›an sich‹.[47] In jedem Fall erweitern sie die Möglichkeiten der spezifischen Ausgestaltung von zeitlichen Strukturen mittels nuancierter Kontraste.

In diesem Zusammenhang lässt sich folgende Hypothese aufstellen: Wird das ungleichmäßige Timing von Grundschlagsunterteilungen als rhythmisch-expressive Abweichung von einer gleichmäßigen Referenzstruktur generiert und wahrgenommen, so sollten Stücke mit stark ungleichmäßiger Subdivision größere Variabilität im Timing aufweisen als annähernd ›gerade‹, von der Referenzstruktur nur wenig abweichende Aufführungen. Wenn aber dies unzutreffend und die alternative Hypothese eines metrischen Status nicht-isochroner Subdivisionen zutreffend ist, dann sollte die Variabilität des Timings keine gravierenden Unterschiede zwischen isochronen und nicht-isochronen Stücken zeigen.

Befunde

Alle drei Stücke im Korpus basieren auf metrischen Zyklen mit vier bzw. acht exakt gleichmäßigen Grundschlägen. Das ungleichmäßige Timing der ternären Subdivision bildet stabile Muster, die sich in jedem Beat einer Aufnahme wiederholen und sich über die verschiedenen Aufnahmen eines Stückes hinweg als konsistent erweisen. In Manjanin und Woloso zeigt sich ein stark ausgeprägtes ›kurz–mittel–lang‹-Pattern (KLL), mit Mittelwerten von ungefähr 25:35:40.[48] In Maraka handelt es sich um ein schwach angedeutetes ›lang–kurz–lang‹, dessen Mittelwerte von etwa 35:30:35 nur geringfügig von einer isochronen Unterteilung abweichen (Abb. 7). Augenfällig ist der Unterschied beider Muster besonders im Timing der zweiten Subdivision, die in den Stücken Manjanin und Woloso wesentlich früher erfolgt als im Stück Maraka. Man beachte, dass nach etwa einem Drittel der Dauer des Grundschlags (im Bereich um 33%) in den Stücken Manjanin und Woloso überhaupt keine Anschläge erfolgen, weil die Artikulationen der zweiten Subdivision sämtlich im Bereich zwischen 20% und 30% stattfinden.

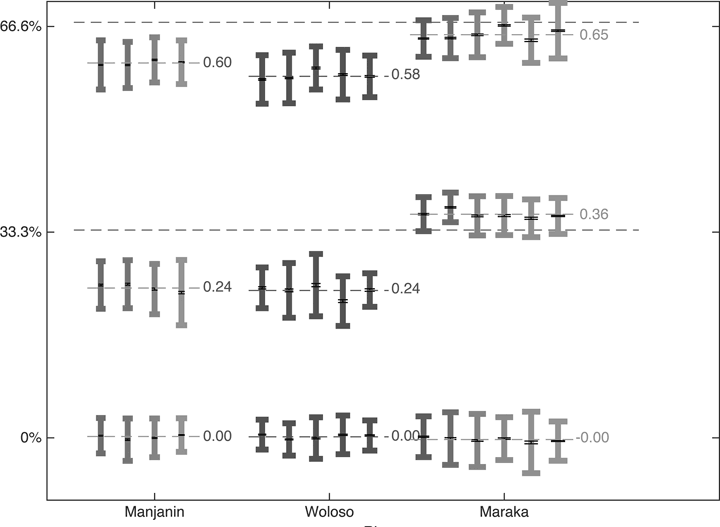
Abbildung 7: Mittelwerte und Variabilität (Standardabweichung als Fehlerbalken) der Onset-Timings relativ zur Beat-Spanne (=100%) (y-Achse),
getrennt nach Aufnahmen je Stück (x-Achse). (Quelle: Polak/London/Jacoby 2016, Fig. 5)

Im Zusammenhang unserer Fragestellung können die Stücke Manjanin und Woloso mit ihrem prägnanten KLL-Timing als Beispiele für stark ungleichmäßige Grundschlagsunterteilung gelten. Im Vergleich dazu ist die Subdivision in Maraka als annähernd gleichmäßig einzuschätzen.

Die Abbildung 8 zeigt in Form eines Histogramms je Stück die genaue Verteilung sämtlicher Onsets im Verlauf der Beat-Spanne. Die steilen Kurven weisen artikulierte Spitzen und tiefe, auf null absinkende Täler auf. Die Breite der Täler zeigt an, dass geraume Abschnitte der Beat-Spanne gar nicht für Anschläge genutzt werden, was vermutlich die Wahrnehmung der Subdivisionsspannen als diskrete metrische Kategorien unterstützt. Angesichts der Tatsache, dass die Abbildung die Timings verschiedener individueller Spieler, Ensembleparts, Instrumente und Phrasentypen in verschiedenen Aufnahmen bei verschiedenen Tempi aggregiert, zeugt die Prägnanz der Verteilungskurven von einer ausgesprochen hohen Konsistenz des Timing-Verhaltens. Im Hinblick auf unsere Fragestellung ist wichtig, dass die Kurven aller Stücke etwa gleichermaßen prägnant wirken. Tatsächlich ist die Variabilität der Grundschlagsunterteilung in allen drei Stücken ähnlich niedrig; die Standardabweichung der Durchschnittswerte beträgt jeweils 2,5–3,5% der lokalen Beat-Spanne.[49]

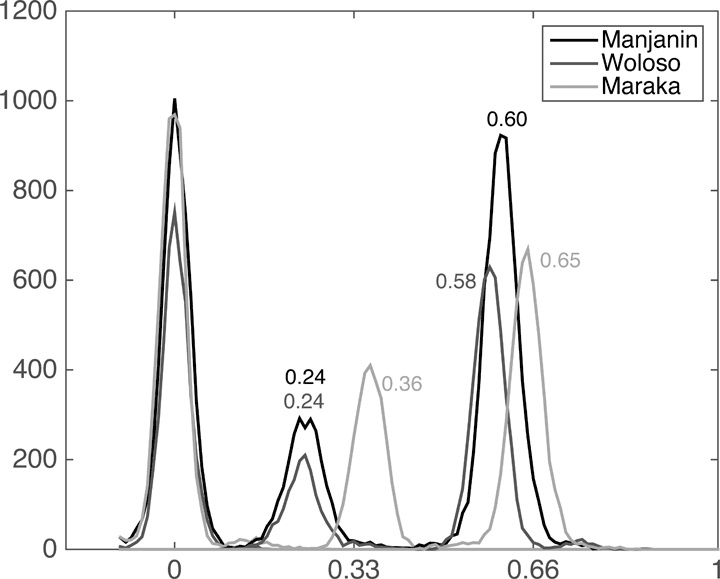
Abbildung 8: Histogramm der Onset-Timings in Relation zur lokalen Beat-Dauer, getrennt nach Stücken. Die y-Achse zeigt die Anzahl der Events, die x-Achse
die Beat-Spanne. Alle Schläge aller Ensemble-Parts aller Aufnahmen eines Stück erscheinen aggregiert. (Quelle: Polak/London/Jacoby 2016, Fig. 4)

Um die Eigenschaften der Ensemble-Synchronisation zu erfassen, vermessen wir das Ausmaß, die Muster und die Variabilität der durchschnittlichen Asynchronien, die zwischen den Anschlägen verschiedener Ensemble-Mitglieder in derselben metrischen Position auftreten. Wir berechnen zunächst für jede Subdivision in jeder Aufnahme den Mittelwert aller Onsets und kalkulieren dann die durchschnittlichen Asynchronien jedes Ensemble-Parts in Bezug auf diese virtuelle Referenz. Im gesamten Korpus beträgt die mittlere Asynchronie nur etwa 2–3% der Beat-Spanne, was je nach Tempo einer absoluten Dauer von nur 6–12 ms entspricht. Trotz dieses ausgesprochen geringen Umfangs zeigen die Asynchronien ein Muster der Phasenverschiebung zwischen den Instrumenten: Die erste Djembe setzt ihre Anschläge minimal vor dem Mittelwert, die Begleitinstrumente (zweite Djembe und zweite Dundun) dahinter (Abb. 9). Dieses zeitliche Vorangehen der Hauptstimme findet sich auch in europäischer Kammermusik (melody lead)[50], während Solisten im Jazz auch hinter der Rhythmusgruppe spielen können (laid back)[51].

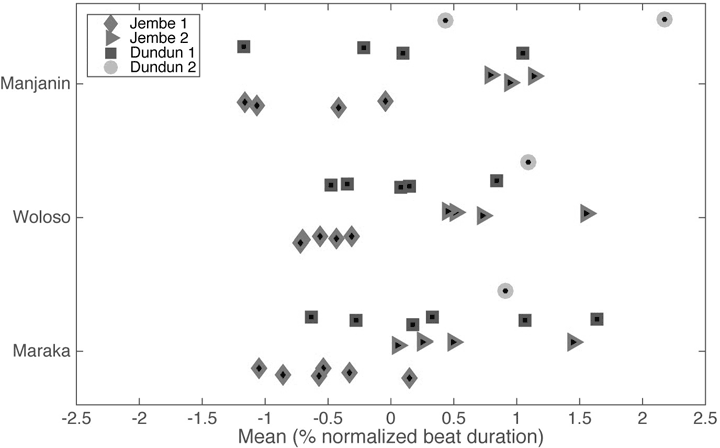
Abbildung 9: Durchschnittliche Asynchronien zwischen den Ensemble-Parts, gruppiert nach Stücken und innerhalb der Stücke nach Instrumenten. Die Symbole eines Instruments innerhalb eines Stücks sind vertikal ganz leicht voneinander abgesetzt, um etwaige Überlappungen nicht unkenntlich zu machen. Jedes Symbol markiert den Durchschnittswert eines Instruments in einer Aufnahme des jeweiligen Stücks. Der Nullpunkt auf der x-Achse markiert den Mittelwert aller Instrumente,
negative und positive Werte bedeuten Zeitpunkte davor bzw. danach. (Quelle: Polak/London/Jacoby 2016, Fig. 7)

Die Größenordnung der auftretenden Asynchronien zeigt keine statistisch signifikanten Unterschiede zwischen den Stücken.[52] Die hohe Präzision der Ensemble-Synchronisation in der Aufführung von Djembe-Musik ist demnach nicht abhängig von der Isochronie der Grundschlagsunterteilung. Standardabweichungen von nur 1,5–3,2% der lokalen Beatspanne (maximal 20 ms) verifizieren, dass das niedrige Ausmaß der durchschnittlichen Asynchronie nicht etwa durch Ausmitteln höherer positiver und negativer Werte entsteht (Abb. 10). Die Asynchronien in Manjanin sind minimal stärker variabel als in Woloso und Maraka[53], aber auch hier tritt kein qualitativer Unterschied zwischen den drei Stücken zutage. Erwartungsgemäß zeigt dagegen die erste Djembe markant höhere Werte als die anderen Instrumente. Die erste Djembe hat mehr verschiedene und stärker variierbare melo-rhythmische Phrasen zur Verfügung als die anderen Ensemble-Parts, was sich in der etwas höheren Variabilität des Timings niederschlägt.

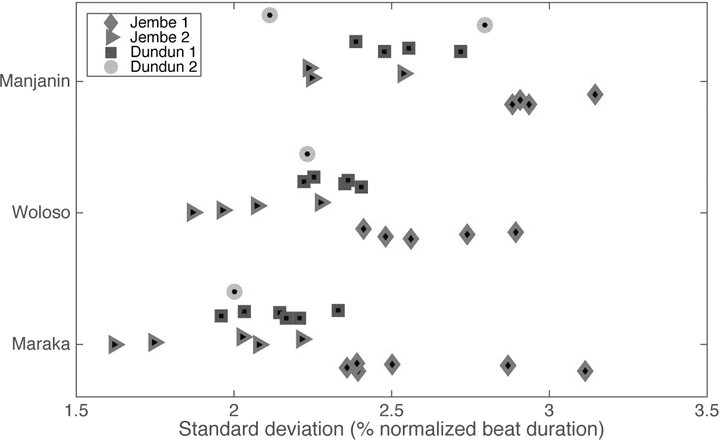
Abbildung 10: Standardabweichungen der mittleren Asynchronien zwischen Ensemble-Parts,
gruppiert nach Stücken und Instrumenten. (Quelle: Polak/London/Jacoby 2016, Fig. 8)

Diskussion

Das Timing der Grundschlagsunterteilung im Korpus ist hoch präzise und stabil; die Synchronisation der Ensemble-Parts ist deutlich enger als etwa in europäischer Kammermusik und im Jazz.[54] Dabei zeigen sich kaum quantitative und keine qualitativen Unterschiede zwischen den Stücken mit gleichmäßiger und ungleichmäßiger Grundschlagsunterteilung. Auch die geringen quantitativen Unterschiede weisen nicht systematisch darauf hin, dass das Timing nicht-isochroner Stücke variabler ausfällt als das isochroner. Die Hypothese, dass die ungleichmäßigen Grundschlagsunterteilungen in Manjanin und Woloso als rhythmisch-expressive Abweichung von einer gleichmäßigen Referenzstruktur generiert und wahrgenommen werden, ist inkonsistent mit diesem Befund.

Teilnehmende Beobachtungen des Autors Polak im Rahmen ethnographischer Feldforschung zeigen an, dass malische Musiker*innen, Tänzer*innen und Publika ungerade ebenso wie gerade Grundschlagsunterteilungen als zugänglich, verlässlich und ›natürlich‹ empfinden. So verwenden etwa Kinder bei ihren spielerischen Aufführungen schon in sehr frühem Alter ungerade Subdivisionen, ohne sich etwa zunächst vermeintlich einfachere, ›gerade‹ Spielweisen zurechtzulegen. Jugendliche Nachwuchsensembles gebrauchen dieselben Timing-Pattern wie ihre erwachsenen Vorbilder, zwar mit etwas höherer Variabilität[55], aber nie mit einer Tendenz zur Isochronie. Erfahrene Berufstrommler sind auf Nachfrage oftmals nicht in der Lage, annähernd ›quantisierte‹ Versionen zu präsentieren. Diese Beobachtungen stützen die alternative Hypothese, dass die untersuchten, stark ungleichmäßigen Grundschlagsunterteilungen in Mali nicht als expressive Timing-Variationen einer isochronen Referenz entstehen, sondern eigenständig metrische Referenzstrukturen konstituieren.

Unsere Befunde widersprechen der weitverbreiteten Annahme, metrische Prozesse (z.B. Projektion, Beat-Induktion, Pulsation oder Oszillation) beruhten notwendig auf der Wahrnehmung isochroner Periodizitäten. Gegen letztere Annahme spricht allerdings auch die weite Verbreitung nicht-isochroner Grundschlagsfolgen, an deren metrischer Funktionalität kein Zweifel besteht. Von Springar-Tänzen in Norwegen über Aksak-Rhythmen in Bulgarien bis hin zu den Chappu Talas der karnatischen Musik lassen sich dafür zahlreiche Beispiele anführen.[56] Erin Hannon und Kolleg*innen verifizierten beispielsweise die metrische Funktionalität nicht-isochroner Beat-Folgen der Dauernverhältnisse 2:2:3. In einer Reihe von Experimenten wiesen sie nach, dass zwar Versuchspersonen mit kulturellen Hintergründen aus Südosteuropa, der Türkei und Indien derlei nicht-isochrone Beat-Folgen kognitiv ebenso gut verarbeiten wie isochrone, nicht aber Personen aus Nordamerika ohne diese Hintergründe. Die Voraussetzung kultureller Vertrautheit bzw. das Fehlen derselben macht hier den entscheidenden Unterschied aus.[57] Diese Forschungen zeigen zusammen mit unseren Befunden, dass Isochronie weder auf der Ebene des Beat noch auf jener der Subdivision eine notwendige Voraussetzung für metrische Funktionalität darstellt.

Realistisch erscheint allerdings, ein gewisses Maß an rhythmischer Regelmäßigkeit als Voraussetzung anzunehmen. Ein erster Vorschlag zur Bestimmung dieses Maßes ist die Forderung einer ›maximal gleichmäßigen‹ Verteilung von Ereignissen in einem gegebenen metrischen Rahmen (maximal evenness).[58] Die erwähnte 2:2:3-Beatfolge entspricht beispielsweise einer maximalen Verteilung der drei Grundschläge über einen Zyklus von sieben Subdivisionen. Die Definition eines größten gemeinsamen Teilers ist jedoch problematisch, wenn die zu verteilende Ungleichmäßigkeit auf der Subdivisions-Ebene liegt. Die oben beschriebenen Dauernverhältnisse von etwa 25:35:40 (oder auch 24:38:38, im Sinne einer Quantisierung des KLL-Patterns) haben zum Beispiel keinen gemeinsamen Teiler, der bei Weitem nicht zu klein wäre – sprich: zu schnell –, um als metrische Pulsation wahrnehmbar zu sein. Die Bestimmung der notwendigen Regelmäßigkeit ungerader metrischer Grundschlagsunterteilungen wird also auf andere mathematische oder qualitative Eingrenzungen zurückgreifen müssen.

Studie 3: Ensemble-Synchronisation

Hintergrund und Hypothese

Menschliches Verhalten zeigt eine starke Neigung, periodisch-repetitive Bewegungsformen gemeinsam und synchron auszuüben. Dies betrifft so verschiedenartige Tätigkeiten wie Fortbewegung (Marschieren, Rudern), manuelle Arbeit (Dreschen, Sägen, Hämmern), den Transport besonders schwerer Gegenstände (›Hau-Ruck!‹), Spiel (Seilspringen, Klatschspiele), Drill, Musik, Tanz und Ritual.[59] Die Synchronisationsleistungen von Instrumentalensembles erscheinen dabei als besonders komplex, präzise und gleichzeitig flexibel. Die Mitglieder eines Ensembles passen ihr Timing fortlaufend an, um natürliche Schwankungen auszugleichen und gemeinsame Intentionen, zum Beispiel einen Tempo-Wechsel, zu verfolgen.[60]

Abbildung 11 zeigt zwei aufeinanderfolgende Subdivisionen im Spiel eines Djembe-Trios. In Subdivision 1 liegt der Anschlag des Spielers 3 zwischen 20 und 30 ms hinter denen der Spieler 1 und 2 zurück, in Subdivision 2 fallen die Asynchronien geringer aus. Hat der Spieler 3 ein fehlerhaftes ›Zu-spät-Kommen‹ seines ersten Schlags wahrgenommen und den zweiten korrigierend angepasst? Oder passten sich umgekehrt die Spieler 1 und 2 dem Timing des Spielers 3 an? Oder entsprach der späte erste Schlag von Spieler 1 einer musikalischen Intention, z.B. einer besonderen Phrasierung? Aus den Asynchronien nur zweier Subdivisionen oder auch einiger metrischer Zyklen lassen sich Antworten auf diese Fragen nicht erschließen. In größeren Datensätzen für ausgedehnte Passagen lassen sich jedoch Kreuzkorrelationen über benachbarte metrische Positionen hinweg berechnen und daraus das Ausmaß abschätzen, in dem einzelne Ensemblemitglieder einander führen oder folgen.

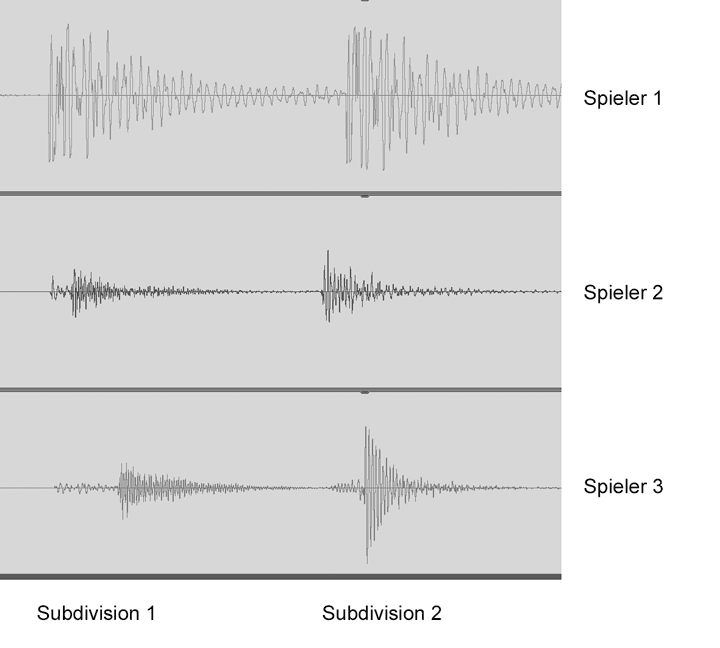
Abbildung 11: Screenshot der sechs Anschläge eines Djembe-Trios während zweier Subdivisionen

Ein noch junger Teilbereich der Aufführungspraxis- und Interpretationsforschung versucht, durch statistische Modellierung des Timings der Ensemblemitglieder die Mechanismen verstehen zu lernen, die der Synchronisationsleistung zugrunde liegen. Die vorherrschende Fragestellung betrifft die vermutete Tendenz bestimmter musikalischer Rollen, Führung auszuüben. Dem liegt die verbreitete Annahme zugrunde, dass stabile Beziehungen der Führung und Gefolgschaft von Vorteil für besonders komplexe Synchronisationsleistungen seien, zum Beispiel für Ensemblemusik.[61] Diese Annahme einer hierarchischen Struktur wird nicht zuletzt auch von vielen Musiker*innen geteilt.[62] Erste empirische Befunde weisen jedoch in eine andere Richtung. Die Untersuchung von Klavierduetten ergab keine Führungsrolle der Melodiestimme gegenüber der Begleitung, sondern wechselseitige Timing-Anpassungen von ausgeglichener Häufigkeit.[63] Studien professioneller Streichquartette zeigten zwar eine gewisse Führungsfunktion der ersten Violine, daneben aber auch wechselseitige und netzwerkartig verteilte Anpassungsvorgänge.[64] Offenbar hängt die Synchronisation zumindest kleiner Ensembles stark auch von Selbstorganisation und Teamwork ab.

Das Djembe-Ensemble eignet sich methodisch zur Erweiterung dieses Forschungsfelds, da jedem Instrument eine distinkte musikalische Rolle zugeordnet ist und sich die perkussiven Onsets präzise bestimmen und analysieren lassen. Darüber hinaus eröffnen sich auch thematisch interessante Perspektiven. Die erste Djembe spielt die melo-rhythmische Hauptstimme, verfügt über die größten spielerischen Freiheiten und verlangt den höchsten Grad an Kompetenz. Spieler der ersten Djembe erwerben außerdem höhere Bekanntheitsgrade als ihre Kollegen, erhalten höhere Honorare und leiten das Ensemble häufig auch in organisatorischen und ökonomischen Belangen.[65] Somit lässt sich die Rolle der ersten Djembe eindeutiger noch als jene der ersten Violine im Streichquartett als eine musikalische Führungsrolle charakterisieren. Dies bringt auch die lokale Terminologie zum Ausdruck, welche die erste Djembe wörtlich als ›Mutter-Djembe‹ anspricht und von der zweiten Djembe abgrenzt, deren Bezeichnung ›Kinder-Djembe‹ lautet.[66] Zwar können sich diese Begriffe auch auf die physikalische Größe der Instrumente und das Lebensalter der Spieler beziehen: Historisch wurde tendenziell das Instrument mit dem kleineren Felldurchmesser für die Begleitrolle der zweiten Djembe eingesetzt und es waren jugendliche Lehrlinge, die sie spielten. Allerdings hat sich das Verhältnis von Felldurchmesser und Rollenzuordnung aufgrund technischen und ästhetischen Wandels umgekehrt: Heute benutzt der Spieler der ›Mutter-Rolle‹ oftmals das kleinere Instrument, weil es sich leichter mit der angestrebten, sehr hohen Spannung versehen lässt.[67] Auch ist es durchaus üblich, dass sich zwei erfahrene Instrumentalisten an der ersten und zweiten Djembe abwechseln. Wenn ein Spieler der ersten Djembe sich etwa aus Gründen der körperlichen Ermüdung von seinem Begleiter in der Rolle des Solisten ablösen lassen möchte, so ruft er diesem einfach zu: »Spiel [die] Mutter[rolle]!«[68] Der Sprachgebrauch ist also teilweise unabhängig vom Alter der Spieler und der Größe der Instrumente, was nahelegt, dass vor allem ein hierarchisch konzipiertes Verhältnis der beiden musikalischen Rollen gemeint ist.

In diesem musikalischen Kontext, da der ersten Djembe eine klar hierarchisierte Führungsrolle zugeschrieben wird, lässt sich folgende Vorhersage treffen: Schließt die Führungsrolle der ersten Djembe den Aspekt der Ensemblesynchronisation mit ein, so sollten die Begleitstimmen (zweite Djembe und zweite Dundun) und auch die Timeline (erste Dundun) sich im Mikrotiming nach der ersten Djembe richten. Sollte dies nicht der Fall sein, so wäre zu erörtern, inwieweit das Konzept der Führung analytisch geeignet ist, das Synchronisationsverhalten in Ensembleaufführungen zu beschreiben und zu erklären.

Methoden und Befunde

Wir greifen zwei Ansätze zur statistischen Modellierung der Richtung und Stärke von Timing-Anpassungen zwischen Ensemblemitgliedern auf.

Das Modell der linearen Phasenkorrektur

Das Modell der linearen Phasenkorrektur wurde ursprünglich für die Untersuchung der einseitigen Synchronisation einer Person mit einem Metronom in sogenannten Tapping-Experimenten entworfen[69] und jüngst für den Bereich der Ensemble-Synchronisation weiterentwickelt.[70] Die Kernidee des Modells ist, dass jedes Ensemblemitglied die Asynchronien zwischen seinen eigenen Noteneinsätzen und denen der anderen Mitglieder als geringfügige Phasenverschiebung wahrnimmt und versucht, gleich mit der nächsten Note zu korrigieren (vgl. Abb. 12).

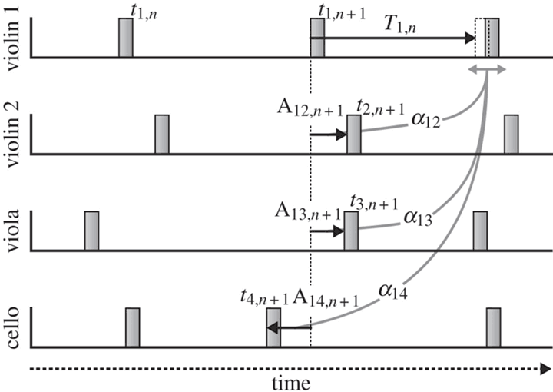
Abbildung 12: Schematisches Modell der linearen Phasenkorrektur aus Sicht der ersten Violine in einem Streichquartett. Die gestrichelte Vertikale markiert die Gegenwart, T_1,n ist das zu modifizierende Inter-Onset-Intervall. Im mathematischen Modell berücksichtigt, aber graphisch nicht dargestellt ist die Vorannahme eines unabhängigen internen Zeitgebers für jede/n Spieler*in. Das Modell beschreibt die Modifikation der vorläufigen, vom Zeitgeber generierten Erwartung (in der Abb. aus Sicht der ersten Violine). Diese ergibt sich zum einen aus den aktuell wahrnehmbaren Asynchronien (A_12,n+1, A_13,n+1, A_14,n+1), zum anderen aus
drei Konstanten (α₁₂, α₁₃, α₁₄), die angeben, wie stark die Asynchronie der jeweiligen Beziehung auf das eigene Timing rückwirkt (correction gain).
Die Bestimmung der Konstanten ist das Ziel des Modells. (Quelle: Wing u.a. 2014, Fig. 1)

Wir berechnen für jedes Ensemblemitglied die Phasenkorrektur gegenüber allen anderen Mitgliedern nach folgender Formel: I_k = Σ_jα_jA_j,k + T_k + M_k − M_k−1 (vgl. Abb. 13). α_j ist die zu berechnende Phasenkorrekturkonstante in Bezug auf andere Spieler j; A_j,k sind die Asynchronien des fokussierten Spieler gegenüber anderen Spielern; T_k, M_k repräsentieren zufällige Schwankungen, die sowohl für den internen Zeitgeber als auch für die Bewegungsausführung anzunehmen sind.[71]

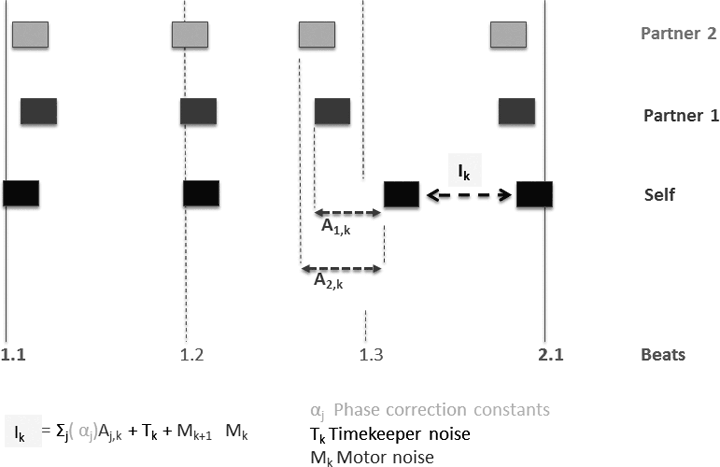
Abbildung 13: Modell der linearen Phasenkorrektur zwischen einem Ensemblemitglied (Self) und seinen Partnern. Die vertikalen Linien kennzeichnen virtuelle metrische Positionen (Grundschläge: durchgezogene Linien; Subdivisionen: gestrichelte Linien). Die Rechtecke repräsentieren die Anschläge dreier Ensemble-Mitglieder, die jeweils mehr oder weniger stark von den metrischen Erwartungen abweichen. I_k ist das gegenwärtig fokussierte Inter-Onset-Intervall eines Spielers (Self).
A_1,k und A_2,k bezeichnen die unmittelbar vorausgehenden, als Einflussfaktoren hypothetisierten Asynchronien
zwischen dem fokussierten Mitglied (Self) und seinen Ensemble-Partnern 1 und 2.

Um die Interaktionen eines Ensembles zu erfassen, wird das Modell auf alle Self-Partner-Paare in je beide Einflussrichtungen angewandt. Wir präsentieren die Ergebnisse als Mittelwerte je Ensemblegröße (Abb. 14). Pfeile kennzeichnen die Richtung und den Stärkegrad der Anpassung: Die Stimme am Pfeilanfang passt sich der Stimme an, in deren Richtung die Pfeilspitze weist; die relative Stärke der Anpassungsbeziehungen ist durch die Pfeilbreite gekennzeichnet. Aus Gründen der Übersichtlichkeit zeigen wir nur die jeweils stärksten Anpassungsbeziehungen und lassen schwächere unberücksichtigt.

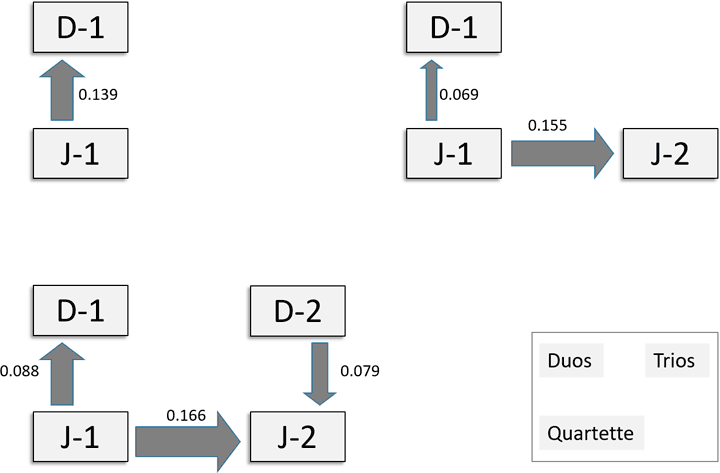
Abbildung 14: Schematische Darstellung der Mittelwerte der stärksten Anpassungsbeziehungen, getrennt nach Ensemblegrößen (Duett, Trio, Quartett). Die graduelle Stärke der Anpassungsbeziehungen wird mit einem Wert zwischen 0 und 1 beziffert, wobei der Wert 1 die einseitige Anpassung in allen erfassten Korrelationen zweier Ensemblemitglieder bedeuten würde. D1 = Dundun 1, J1 = Djembe 1, D2 = Dundun 2, J2 = Djembe 2.

In der kleinsten Besetzung, dem Duett, passt sich die Djembe häufig der Dundun an, nicht aber umgekehrt die Dundun an die Djembe. Im Trio richtet sich die erste Djembe ebenfalls nach der Dundun und, stärker noch, auch nach der zweiten Djembe. Im Quartett wirkt als drittstärkste Bindekraft die Anpassung auch der zweiten Dundun an die zweite Djembe. Das Hauptergebnis ist, dass sich die erste Djembe – die Hauptstimme – als anpassungsfreudigster und nicht etwa als führungsstärkster Ensemble-Part erweist. Die meiste Orientierung bietet dabei die zweite Djembe.

Das Modell der Granger-Kausalität

Das Modell der Granger-Kausalität wurde erst jüngst aus der wirtschaftswissenschaftlichen Zeitreihenanalyse in die musikalische Synchronisationsforschung übernommen.[72] Es vergleicht das Ausmaß, mit dem Schwankungen einer Zeitreihe aus vorhergehenden Schwankungen derselben Zeitreihe vorhergesagt werden können, mit dem Ausmaß der zutreffenden Vorhersagen unter Einbezug des Einflusses einer zweiten Zeitreihe.[73] Ist der zweite Wert höher als der erste, so kann ein kausaler Einfluss angenommen werden, obwohl die mathematischen Berechnungen jeweils nur Korrelationen erfassen, denn als hypothetisch erklärende Schwankungen werden nur solche getestet, die den erklärten zeitlich vorausgehen.

Wir folgen einem Vorschlag von Glowinski und Kollegen (2012) und berechnen die Granger-Kausalität zwischen zwei Ensemblepartnern durch einen Abgleich zweier verschiedener linearer Modelle: Das einfache Eigen-Modell (self model) berücksichtigt nur die Inter-Onset-Intervalle des fokussierten Ensemblemitglieds (I_k = xI_k−1 + n_k), während das Interaktions-Modell (joint model) zusätzlich zum Eigen-Modell auch den möglichen Einfluss eines Partners erfasst (I_k = xI_k−1 + yA_k + m_k). Im Interaktionsmodell gilt: I_k ist das Inter-Onset-Intervall des fokussierten Ensemble-Mitglieds zum Zeitpunkt k und A_k ist die Asynchronie zwischen den beiden Mitgliedern; m_k, n_k sind unabhängige und zufällige Schwankungen, für die wir jeweils Normalverteilung annehmen. Die freien Parameter des Modells (x, y) können mittels Standardregression den Daten angepasst werden. Zur Berechnung des Granger-Index (G = 1 − SS_joint/SS_self) sei SS_self bzw. SS_joint die Variabilität von I_k, erklärt durch das Eigen- bzw. Interaktionsmodell (vgl. Abb. 15).

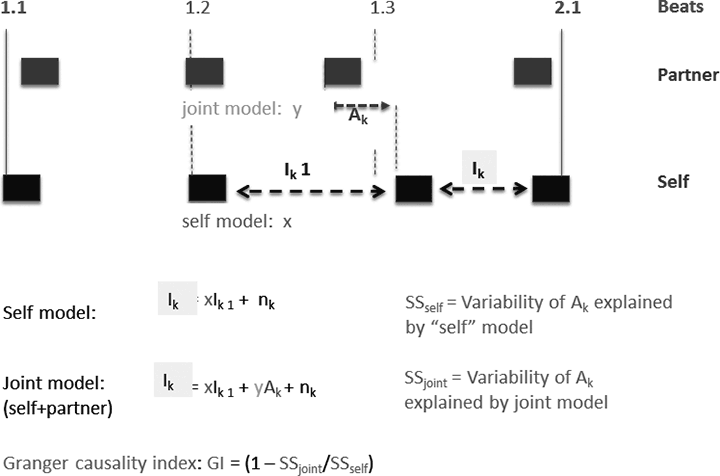
Abbildung 15: Modell der paarweisen Granger-Kausalität zwischen einem Ensemblemitglied (Self) und einem Partner. I_k ist das gegenwärtig fokussierte
Inter-Onset-Intervall eines Spielers (Self), A_k die unmittelbar vorausgehende Asynchronien zwischen Self und Partner.

In Abbildung 16 stellen wir die Resultate des Granger-Modells den oben (Abb. 14) dargestellten Ergebnissen des Phasenkorrektur-Modells gegenüber. Wiederum zeigen wir nur eine Auswahl der stärksten Anpassungsbeziehungen für jede Ensemblegröße. Sowohl für das Duett als auch für das Trio stimmen die Ergebnisse beider Modelle qualitativ überein: Die erste Djembe passt sich an die erste Dundun und an die zweite Djembe an. Im Quartett hebt das Granger-Modell hingegen die Anpassung der ersten Djembe auch an die zweite Dundun als drittstärkste Bindekraft hervor, während das Phasenkorrektur-Modell eine Anpassung der zweiten Dundun an die zweite Djembe ergab.

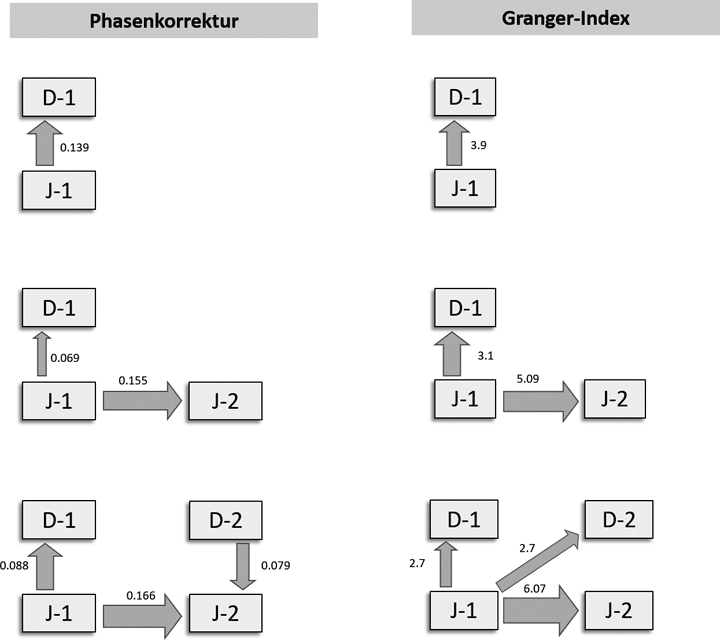
Abbildung 16: Schema der stärksten Anpassungsbeziehungen, getrennt nach Ensemblegrößen (von oben nach unten: Duette, Trios und Quartette) und berechnet mit zwei verschiedenen statistischen Modellen (links: lineare Phasenkorrektur, rechts: Granger-Kausalität). D1 = Dundun 1, J1 = Djembe 1, D2 = Dundun 2, J2 = Djembe 2.

Diskussion

Der Hauptbefund unserer Studie ist das Anpassungsverhalten der ersten Djembe, die sich bei der Ensemble-Synchronisation auf ihre Partner verlässt. Die weitgehende Übereinstimmung der Resultate zweier verschiedener Verfahren zur statistischen Modellierung (Phasenkorrektur und Granger-Kausalität) unterstreicht beider Validität. Das Ergebnis ist insofern plausibel, als die hoch variable Hauptstimme der ersten Djembe als Zeitgeber vermutlich nicht gut geeignet wäre. Zum einen machen komplizierte Rhythmen, virtuose Ornamente und unvorhersehbare Wendungen es den Ensemble-Partnern schwer, ihr kontinuierlich aufmerksam zu folgen. Zum anderen hätte die vergleichsweise hohe Variabilität im Timing der ersten Djembe (vgl. oben, Studie 2, Abb. 10) sicher eine größere Variabilität auch des Ensemble-Timings zur Folge.

Auf ähnliche Weise struktur-funktionalistisch orientierte Erklärungen bringen auch malische Musiker in Gesprächen und Interviews zum Ausdruck. Spieler der ersten Djembe, so ein narrativer Topos, entfernen sich während solistischer ›Ausflüge‹ oft auf schwer berechenbare Weise vom Ensemblerhythmus. Den Begleitern obliegt es, dem Solisten jederzeit eine verlässliche Plattform zur ›Rückkehr‹ zu gewährleisten. Daher sollten Dundun- und zweite Djembe-Spieler besser nicht mit uneingeschränkter Aufmerksamkeit dem Solisten folgen, so ein oft gehörter Ratschlag, denn das könnte sie zu Fehlern verleiten. Vielmehr sollten sie vor allem jeweils bei sich selbst und untereinander verbunden bleiben. Allerdings wird dieser Ratschlag gerne mit dem Hinweis verbunden, dass man dennoch ständig ein offenes Ohr für alle Stimmen im Ensemble haben sollte.

Schon Studien europäischer Kammermusik erwiesen sich als nicht oder nur teilweise konsistent mit der Hypothese, Ensemble-Synchronisation bedürfe der hierarchischen Führung durch eine Person bzw. musikalische Rolle. In Klavierduetten wurden reziproke Timing-Anpassungen und in Streichquartetten verschiedene Mischungen von Führung der ersten Violine und nicht-hierarchischer Wechselseitigkeit festgestellt.[74] Unsere Befunde gehen noch darüber hinaus und kehren die ursprüngliche Annahme um: Die Führungsrolle, die die erste Djembe in vieler Hinsicht im Ensemble spielt, geht mit einer ›Gefolgschaftsrolle‹ im Bereich der Ensemble-Synchronisation einher. Eine kohärente Führungsrolle – eine Stimme im Ensemble, die auf allen Ebenen des Verhaltens die Fäden in der Hand hält – existiert nicht in der Djembe-Musik. Zwar kann man sagen, bei der Ensemble-Synchronisation übernehme die Begleitung (zweite Djembe) die Führung und die Führstimme (erste Djembe) leiste ihr Gefolgschaft. Aber paradoxe Fügungen wie ›Begleitung als Führung‹ und ›Führung als Gefolgschaft‹ deuten doch auch an, dass das Konzept der Führung (leadership) dem Prozess der Ensemble-Synchronisation nicht angemessen ist. Anpassung ist der Verhaltensaspekt, der Synchronisation eigentlich ermöglicht. Das Beispiel des Djembe-Ensembles zeigt, dass ›Referenz für Anpassungsverhalten‹ nicht notwendig mit ›Führung‹ gleichzusetzen ist.

Fazit

Unsere Korpusanalysen einer westafrikanischen Musikform verstehen sich als Beitrag zur verstärkten Anerkennung kultureller Diversität in der empirischen Rhythmusforschung. Die vorgelegten Befunde begründen Modifikationsbedarfe sowohl der allgemeinen, psychologisch orientierten Rhythmustheorie universalistischen Anspruchs als auch der musikethnologisch fundierten Theorie afrikanischer (subsaharischer) Rhythmik. Studie 1 widerlegte die im Rahmen euro-amerikanischer Musikforschung vorherrschende Annahme eines universellen Kongruenzstrebens im Verhältnis von Rhythmus und Metrum und bestätigte hierin Einsichten der afrikanistischen Musikforschung. Studie 2 belegte die Möglichkeit einer metrischen Funktionalität nicht-isochroner Rhythmen und widerspricht damit der Annahme von Isochronie als notwendiger Grundlage metrischer Prozesse. Während die Resultate der Studie 1 mit der Musikethnologie und gegen eine Tendenz zum Eurozentrismus in der allgemeinen Rhythmustheorie argumentieren, richtet sich das Argument der Studie 2 auch gegen die afrikanistisch-musikethnologische Rhythmustheorie, in der das Axiom metrischer Isochronie ebenso verankert ist wie in der euro-amerikanischen Musikforschung. Die Großregion der west- und zentralafrikanischen Sahel- und Sudanzone, in der nicht-isochrone Grundschlagsunterteilungen verbreitet sind, ist in der afrikanistischen Musikforschung musikanalytischer Ausrichtung unterrepräsentiert.[75] Hier wird deutlich, dass kulturvergleichende Forschungsperspektiven und die Anerkennung kultureller Diversität nicht nur einer Kritik eurozentrischer Annahmen dienen können, wie sie häufig aus der Musikethnologie an die Musikpsychologie und Musiktheorie gerichtet wird, sondern auch einer Überprüfung empirisch unzureichend begründeter Generalisierungen innerhalb der Musikethnologie.

Studie 3 widmete sich der Analyse von Performance-Timing zur Untersuchung von Führungsrollen bzw. Anpassungsverhalten bei der Ensemble-Synchronisation. Dieses Forschungsfeld ist erst im Begriff, sich zu konstituieren. Die bislang untersuchten Ensemble-Typen zählen zum Segment der interpretierenden europäischen Kunstmusik und unser Hauptergebnis, die Anpassungsleistung der Hauptstimme und eine zeitliche Referenzfunktion der Begleitstimmen, kontrastiert mit deren bisherigen Befunden. Es erscheint jedoch wenig wahrscheinlich, dass wir es hier mit einem stil- oder kulturspezifischen, ›djembe-typischen‹ oder ›afrikanischen‹ Phänomen zu tun haben. Plausibler erschiene uns, Hypothesen an die improvisatorische Aufführungspraxis und die im Ensemble stark abgestufte Verteilung von Variabilität (vom strikten Ostinato der Begleitung zur großen Spontaneität der Hauptstimme) zu knüpfen. Sollten diese Faktoren für das Anpassungsverhalten im Djembe-Ensemble verantwortlich sein, so wären ähnliche Befunde etwa in afro-amerikanischen Musikformen zu erwarten, deren Ensembles vergleichbare Beziehungen von Begleit-Parts einerseits und Haupt- bzw. Solostimmen andererseits aufweisen. Das Konzept des ›time-keeping‹ durch Schlagzeug und Bass im Jazz[76] lässt diese Hypothese plausibel erscheinen.