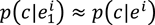Musical Expectancy

1. Introduction

A mind is fundamentally an anticipator, an expectation-generator.[2]

Once a musical style has become part of the habitual responses of composers, performers, and practiced listeners it may be regarded as a complex system of probabilities […]. Out of such internalized probability systems arise the expectations—the tendencies—upon which musical meaning is built […]. The probability relationships embodied in a particular musical style together with the various modes of mental behavior involved in the perception and understanding of the materials of the style constitute the norms of the style.[3]

Musical expectancy is regarded as one of the most central aspects of music perception[4], and as such has received a great deal of scientific attention. The concepts of expectancy and prediction link static analytical approaches in music theory and analysis with the dynamic temporal aspects of the musical listening experience. The core insight that musical experience is (in part) closely linked with the cognitive processing of patterns of expectancy dates back to Leonard B. Meyer’s seminal theory.[5] Prediction and expectancy formation constitute fundamental neurocognitive mechanisms of ongoing, automatic temporal processing of events of all kinds and are coupled with emotional reactions to the forms of expectancy associated with (musical) events.[6] Up to present there is large agreement that a substantial part of musical emotional experience originates in ‘side effects’ of processing likely and unlikely events, fulfilled and unfulfilled predictions. Given its neurocognitive basis, it is barely surprising that music has evolved to make heavy use of various forms of expectancy and predictive processing to trigger strong emotional effects.[7] Supporting this cognitive account is a large body of interdisciplinary recent research bridging psychology, computational modeling, and the neurosciences.[8] The study of the phenomenon of musical expectancy demonstrates successful ways to bridge theoretical/analytical, psychological, neurocognitive, and computational approaches in order to jointly advance our understanding of the foundations of the dynamic experience of musical listening.

Since the recent growth of literature on musical emotion, tension, and expectancy[9], several extensive reviews of cognitive and computational approaches have been published that explain the psychophysiological, neural, cognitive, and computational underpinnings of musical expectancy.[10] Accordingly, the purpose of this contribution is not to reiterate a review of the cognitive bases of musical expectancy that is up to date with this recent series of publications, but to introduce and to relate some of these notions and core underlying ideas to a more general music-theoretical audience in order to illustrate how interdisciplinary interactions between theoretical, computational, and cognitive approaches may be established.

This article is organized as follows: It first introduces core concepts to understand expectancy from a perspective of cognitive model building and discusses theoretic aspects of musical representation and constraints of well-defined models that have important implications for music-theoretical approaches. Departing from this background the article discusses different types of models of expectancy, in particular local Markov models. Using the example of Markov models the article introduces the notions of overfitting and sparsity and illustrates that these notions, that often remain unaddressed in current music-analytical literature, are of fundamental relevance for music-theoretical descriptions in general. The final part of the text analyzes the implications of hierarchical models for the concept of expectancy.

2. Relating Theoretical, Psychological and Computational Perspectives

Fundamentally, expectancy is a core cognitive process (i.e., a partial foundation of musical listening), and not a property of the musical score or of any other representation of musical structure (e.g., MIDI). Although they might be described in terms of music-theoretical constructs, statements about musical expectancy always refer fundamentally to an act of listening associated with underlying neural/mental processes and not to certain structures. Furthermore, discussing expectancy in the context of music analysis implicitly (and inescapably) assumes an underlying cognitive model of listening and expectancy formation that operates in terms of the music-theoretical or music-analytical concepts used. Following on from discussions by Ian Cross, Geraint Wiggins and others, it is crucial to ensure that the foundations of music-theoretical concepts and arguments do not lie in vague forms of folk-psychology[11], but are firmly rooted in psychological, neurocognitive, mathematical and computational foundations.

A description that specifies in detail how elements (derived from music-theoretical concepts and described by a well-defined language) are organized and combined to predict other elements constitutes a (more or less detailed) formal model, which is in essence analogous to the definition of a computational model in the sense of computing well-defined operations on symbolic representations.[12] The notion of formal descriptions that are in essence computational is far older than the arrival of the first electronic computers. Similarly the intent of a numerous (music-)theoretical descriptions and models is (implicitly) computational. Music analytical models, “pen-and-paper” models, syntactic models or (psychological) box models may be conceived of as computational descriptive or explanatory models that just—and crucially—differ with respect to the level of detail and consistency in which they are described or specified.[13] The degree of detail in some music-theoretical approaches is indeed very close to computational modeling[14], particularly in cases that parallel some forms of syntactic analysis in linguistics.[15] The potential for the development of a rich understanding of musical expectancy lies in close collaboration between theoretical and computational approaches.[16] The advantage of concise computational models (and their implementations) over mere theoretical accounts is manifold: The details are fleshed out in terms of the precise nature and representation of all elements involved, as well as the precise order and interaction of all processes involved[17]; the process of implementation frequently leads to the identification of notable inconsistencies and redundancies in the theoretical account; the implementation allows one to verify whether the theoretical predictions are indeed predicted; and whether they are fulfilled or not, given evaluation criteria and evaluation with test cases. The following discussion examines some theoretical accounts of musical expectancy from this background.

3. Expectancy and Underlying Models – Basic Concepts

What, When, and Which Forms of Representation?

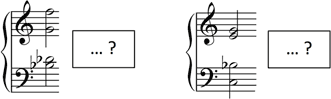
The following paragraphs introduce and exemplify a number of fundamental issues regarding musical expectancy. Consider a simple first simple example in the domain of harmony (see Fig. 1).

Figure 1. Harmonic implication and prediction illustrated by two predictive contexts.

Figure 1 illustrates two simple cases of harmonic expectancies generated by different chords. One might state that a sixte ajoutée chord predicts a subsequent dominant (Fig. 1, left) or, more trivially, that a dominant-seventh chord predicts a major or minor chord the root of which is a fifth below (Fig. 1, right). However, these simple examples involve several implicit assumptions; first of all the ‘what’ question, with which most analysts are concerned. However, expectancy does also involve the ‘when’ aspect. Given a sixte ajoutée chord, when is the dominant expected to enter? At the next bar, the next beat, the (immediate) next event, at an unspecific point in the ‘near’ future? All of these options suggest different assumptions concerning the underlying model of expectancy: Is the element (the ‘what’) dependent on metrical structure, metrical hierarchy, rhythm, the mere sequence of events (i.e., independent of meter), or dependent on the following context (does the model allow for other elements to fall in between; and if so, which ones are defined as structurally important or unimportant)? It is important to note that any answer a music theorist may give inescapably involves an underlying theoretical choice concerning such choices of representation even if it may not be made explicit. Every account of expectancy relies on a well-defined model of expectancy. Crucially, if no model is explicitly defined, its parameters are covert in the analytical process and the account is prone to be incomplete, inconsistent or ill-defined. Each of the options listed above (and their combinations) imply different expectancy models with respect to the postulated components and their interaction.

Turning back to the ‘what’ aspect, does expectancy formation make predictions about the chordal root (C), the chord type (a major chord on C: root and type), the functional category (a dominant), a specific instance of the chord or even a specific voicing? (It is important to keep in mind here that this description of expectancy concerns listening, not the score.) As before, there is no natural, a priori ‘right’ answer to this, and no ‘right’ answer that can be discovered through reflection; the answer depends on the underlying model and involves a decision with respect to the level of representation, the fine-grained or rough resolution, and, more specifically, the purpose of the model. Further, are the input and output of the model of the same type? Does a dominant-seventh chord on G imply a continuation with a C root, a generic chord, or a specific C-major chord? At one theoretical level, it may be appropriate to say that sixte-ajoutée chords imply dominant-seventh sonorities or a dominant function, while at another level more detail may be required. Purely analytical or theoretical approaches require careful design in order to be globally consistent with respect to the level of representation. These points illustrate the role of the chosen representation, the components of the model, and the interaction between these components.

One frequent counter-argument raised against cognitive or computational models is that they involve accounts of music that are overly naïve or simplistic, lack complexity, or are dismissive of important context or musical (philological or music-theoretical) details. While it is always possible to include more detail or raise the level of abstraction, there is no a priori foundation of a ‘right’ level of analytical detail (or the ‘best model’) without reference to a specific purpose or evaluation criterion depending on the purpose.

Depending on the evaluation criterion there is also a trade-off between simplicity and accuracy as well as the problem of overfitting (see below). After all, accounts with greater levels of detail are not necessarily better and may gain only little improvement for the price of massive additional complexity, or they may even turn out with worse descriptive/predictive power, while (seemingly) simple models may have strong predictive power. Highly complex models that account for a large number of different factors/components may further be prone to design mistakes and redundancies when specifying their interaction and be difficult to interpret (which interactions did lead to the observed results?).

Like Borges’s famous “map” “representing” its territory at a 1:1 scale[18], excessive musical detail may impair the interpretability and the use of a music-theoretical account. In the spirit of Borges’s “Del rigor en la ciencia” (“On Exactitude in Science”), imagine the final establishment of an ideal type of a comprehensive 6000-page encyclopedia (any resemblance to real projects or publications purely coincidental) with a finely detailed ‘final’ description of sonata form classified by an abundantly rich variety of historically, philologically and systematically relevant distinctions and parameters, organized into 35 types and subtypes, differentiated in time by single year, in place by shire, organized by the causal web of mutual influence, amongst many other pieces of information. What would a pattern of interaction between type 3, 8 and 12 in two locations and between 1781, 1785 and 1787 mean—once the effort is comprehensively pursued to excavate such a relation—and what would it entail with respect to an account of expectancy of form? What generalizable insight might be drawn from a description with excessive level of detail? The first step to ‘analyze’ such a comprehensive account (say, in the case of teaching it to students or to yourself) would be one of simplification, in other words coming up with a map for the map, i.e. a simple model to cut a swath through the thicket. One instance of a fruitful outcome of the tension between theoretical complexity and stepwise simplification in consequence of theoretical and empirical explorations is found in the recent history of music cognition in terms of the successive simplification of Eugene Narmour’s implication-realization theory that led to fundamental insights into the nature of musical expectancy that are also informative from a music-theoretical perspective.[19]

Incorporating Context-Dependency

Expectancy is further dependent on various kinds of ‘context’: The sixte ajoutée chord or the dominant-seventh chord (Fig. 1) may entail different predictions depending on the underlying tonal or stylistic context. The dominant-seventh chord suggests a much greater variety of possible continuations in works by Schumann or Liszt than in works by Vivaldi, Telemann, or Handel, and may exhibit a much weaker implicative tendency in the context of a Blues scheme. Another common example for style-dependent expectancy is constituted by the added sixth major (or minor) chord, which clearly invokes a subdominant function in the eighteenth century while it may function as a tonic for composers like Claude Debussy or Duke Ellington. This aspect of the overarching (stylistic) context is an implicit or covert assumption in a model of expectancy. How can this context be accounted for in a model?

One way would be to posit a different model for each case: one for common-practice music, one for Jazz, one for Rock, one for the Classical Style, one for Schumann, one for Handel, one for early Beethoven, one for late Beethoven, one for Bach’s Partitas, one for Beethoven’s “Waldstein” sonata, etc. While it may be insightful to study differences or similarities between different stylistic models, this list points at the core distinction between the type of a model and its parameters.

Generally, the definition of a model distinguishes between its parameters and the independent structure of the model. The parameters represent the information that the model operates on (for instance the information encoded in a Markovian transition matrix, that may represent style-specific knowledge about, e.g., chord transitions). While the parameters may be different for each of the above cases, there may be a single type of underlying model of expectancy that is independent of its parameters (such as a Markov model, e.g.,a table of usual root progressions in the sense of Piston, or a tree structure in the sense of hierarchical models). In the case of music-analytical description of features that govern a certain style, it may be beneficial to draw clear distinctions between the model structure and its parameters. Once there is a clear distinction between a model and its parameters, one may examine how the parameters of the model may be inferred from data given. Recent computational models commonly involve methods to infer/learn the parameters from given examples (training data) such that the parameters do not need to be specified by hand but may be flexibly adapted to the ecological properties of the data/corpus it operates on.

The clear definition of a model of expectancy, its parameters and the inference process may be closely related to an overarching notion of (an aspect of) musical competence.[20] If one intends the model to represent cognitively relevant representations that govern musical competence and assumes that the corresponding processes are shared across the members of a community, the unity of the model, its parameter space in conjunction with its acquisition process as well as the corresponding stabilized structures of the music of the community characterize the intersubjectively shared medium[21] of musical communication (e.g.,Western tonality, Middle Eastern maqām, or the North Indian rāga).[22] This understanding makes it possible to undermine purely subjectivist or solipsist accounts of aesthetics or musical forms of private languages by a cognitively founded account of intersubjectivity.[23] From this cognitive perspective arguments about subjectivity of musical listening (an imaginary overly post-structuralist critic may insist to hear iii to be implied by V rather than I which in turn ‘sounds irregular’) may point towards questions that are decidable on an empirical basis: Assuming that a Markov model (see below) is a fair model of musical competence and musical expectancy, given the Markov model and its parameters learned from a corpus of common-practice tonal music the context of a V chord predicts a I chord as the most likely continuation.[24]

The Choice of the Type of Model

Following up on the previous account of a model, one core foundation underlying analytical approaches to musical expectancy concerns the structure of the model, i.e. making explicit how expectancy is derived. One simple way is to define a model based on statistical frequency of occurrence (as above): Find instances of ‘V–x’ in the chosen musical material (the ‘corpus’), count their number, count the instances of ‘V–I’ among them, and divide the latter by the former to arrive at an estimate of the predictive probability based on the frequency counts. This is not far from what Walter Piston’s early account of the table of common root-progressions (Fig. 2) may express, if it were specified with sufficient level of detail and with explicit accounts of the covert underlying assumptions.

Figure 2. Walter Piston’s table of usual root progressions (1948).[25] The table constitutes an early instance of an informal Markov model of root progressions based on musical experience and intuition (or ‘intuitive statistics’).

Note that the notion of such a Markov model rests on the assumption that there is an (accessible) level of representation that allows for comparison and counting (e.g., how to count pitch slides or notes with slight differences in intonation?) and that an estimate of the predicted next event can be determined by frequency counts. The account is independent of style and musical representation (i.e., the choice of building block): It is sufficiently general to be applied to melody, harmony, sequences of drum strokes or North Indian rāga. Crucially, the above specification of the Markov model contains another underlying assumption: that only the immediate context but no larger context[26] is relevant for expectancy (since prediction is only computed in terms of one predictive event, any event preceding this context is not taken into account and hence irrelevant to the model; models that incorporate nonlocal dependencies are discussed below). This model is called a Markov model, and the assumption about the relevant context the Markov assumption, given in mathematical terms as:

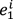
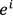
In words: The probability of any event c at the position i + 1 given a context e ranging from the beginning of the piece to position i (written as ) is well approximated by the probability of c, given just the smaller context of the element . Such models, which have been implemented from the 1950s onwards[27], are widespread and still frequently employed today.[28] A recent example of a corpus study of Bach’s chorales provides one possible empirical implementation of a heuristic that approximates harmonic counts and provides an empirical estimate:[29] V–I is roughly seven times more likely than V–vi. The difference is that Piston’s judgments (Fig. 2) about frequency are intuitive[30] (‘regular’ vs. ‘sometimes’ without specification of whether ‘sometimes’ has roughly the same meaning across different rows), while the latter are empirical estimates and based on both a corpus and a detailed replicable and comparable process.[31]

Further, well-defined music-theoretical accounts of expectancy such as Markov models lend themselves to empirical testing and evaluation providing further insight into the process of expectancy formation. For instance, the characterization of harmonic expectancy by progression tables has been tested empirically in studies using probe chord and harmonic continuation paradigms, leading to partial confirmation and partial revision of the theoretical predictions made by Piston.[32]

Different levels of musical expectation

So far, a model of expectancy has been characterized as the combination of the model structure and its (potentially learned or acquired) parameters from which predictions are derived. However, in an endeavor to model expectancy in listening (or interactive cognitive tasks such as improvising), different sources of expectancy have to be accounted for: There are differences between expectations based on our general acquired musical competence and expectations based on particular features of the current piece we are listening to or interacting with. Accordingly, a distinction is required between knowledge driven and online expectancies (or long-term and short-term models according to the terminology by Pearce et al.[33]). These types of expectancy formation may interfere (see below).[34]

Another distinction has to be made regarding levels of expectancy. The cognitive musicology literature commonly assumes three levels of expectancy: data-driven, veridical and schematic/knowledge driven.[35] Data-driven predictions characterize simple musical processes that may not require a foundation in acquisition: an ascending scale, for example, or a simple pattern such as note repetition or alternation.[36] One may further classify accounts of musical processing and prediction based on purely sensory processing as forms of knowledge-free data-driven sources of expectancy.[37] Veridical expectancy refers to cases in which the musical source itself (the piece) is known so that predictions about upcoming events are based on prior knowledge of the (presumed) true source (Fig. 3). Finally, expectancy formation that is neither based on simple patterns nor on prior veridic knowledge of a piece may rely on previously acquired style-specific knowledge or schemata (musical competence), e.g. of harmony or voice leading. The sixte-ajoutée chord above (Fig. 1) constitutes an example of knowledge-driven expectancy acquired by previous experience of tonal music. Crucially, knowledge-driven forms of expectancy are bound to an underlying process of expectancy generation (such as a Markov model or a tree-based model) and a complementary process of knowledge inference and acquisition (implicit learning).[38]

Figure 3. Example of veridical expectancy

The Problems of Overfitting and Sparsity

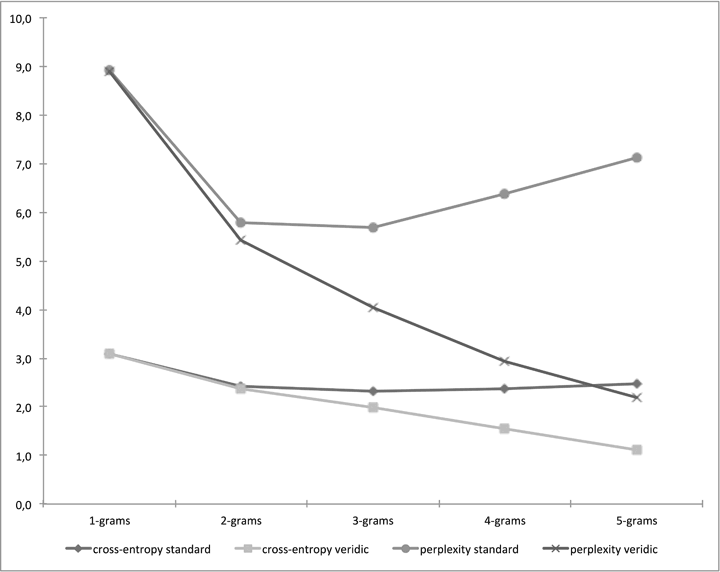
It is a commonplace in computational modeling that descriptions and models do not necessarily get better by adding more information. One example of a study modeling Jazz harmony shall illustrate this.[39] Using Markovian methodologies similar to the ones introduced above, the study implemented n-gram models (amongst others) for the prediction of chord sequences from a large Jazz corpus and compared the performance of models of different context length: The prediction of the next chord was based on mere single-chord frequencies (1-gram model), conditioned on the previous chord (2-gram model), the two previous chords (3-gram model), or the three or four previous chords (4-gram and 5-gram model). These n-gram models were evaluated using a large corpus of harmonic lead-sheet annotations of 1600 Jazz standards.[40] Furthermore, the study compared two forms of evaluation: In the standard case, the corpus of Jazz standards was split into two parts, one of which was used for model training (i.e., for estimating the probability tables used for prediction as outlined above) and one for evaluating each model; in the second veridical case, the training set contained the evaluation set.[41] Figure 4 displays the performance of the different n-gram models under standard and veridical conditions.

Figure 4. Performance of predictive n-gram models of harmony using different context length[42]

As the figure illustrates, the n-gram models of the Jazz corpus reach an optimal performance level for n=2 or n=3. This means that a context of one or two previous chords is optimal for predicting the next chord, whereas a model with a larger context possesses lower predictive power. Hence, more information incorporated into the model does not necessarily improve its performance. To the contrary, larger contexts here contain too many chord sequences specific to individual pieces or individual progressions and thus are not generalizable across a larger set of cases.

A second observation can be made comparing the performance for the veridical vs. the standard case. In the veridical case, in which the test set is included in the training set from which the model parameters are estimated, the performance continuously improves with increasing context length. For the cases of 4- and 5-grams, predictions for chord contexts of three and four chords are compared. These chord progressions are highly individual; since the models have incorporated all the test cases as well, they are good at predicting individual progressions in the test cases. However, this does not entail that these are ‘better’ models: They would generalize poorly similar when confronted with novel progressions as the example of the same models in the non-veridical case illustrates. Although they incorporate a large amount of piece-specific knowledge, by no means does this result in neither improved general harmonic knowledge, nor does it improve the model’s capacity for predicting harmonic progressions. This case constitutes an example in which more detailed harmonic knowledge is even detrimental for a description of harmony with generalized predictive power.[43]

This result is not limited to harmony and transfers to other musical structures. For instance, Marcus Pearce and Geraint Wiggins report a similar finding for the modeling of melodic prediction with n-gram models.[44] This problem is referred to in the computer science literature as the ‘overfitting problem.’ Some models may be over-trained with too much information that does not improve, but rather impairs the description/the inferred knowledge of the structures.

Another related issue concerns the contrasting common problem of sparsity: Even though a Markov or n-gram model may be trained with data from a large number of musical examples, there is still a high likelihood that an application of the model to musical prediction may encounter a context the training materials did not contain and the model has no information about. Given the definition of the Markov model above, it is impossible to derive a prediction for the next event if there is not a single sample case (e.g., how to predict the continuation of [U V W …] if there is no instance of [V W] in the reference data?). This problem occurs frequently in computational modeling[45] and bears theoretical implications for music theory (see below). Commonly, Markov or n-gram models involve specific techniques of ‘zero-escape methods’ and ‘smoothing’ to avoid such cases.[46]

The phenomenon of sparsity, related to the ‘Zipf distribution,’ is a common property of the distribution of events across a large range of natural phenomena, including language and music.[47] Briefly construed, it implies that there is a small number of items that occur very frequently and account for most of the domain while a large number of items occurs highly infrequently[48] (frequency approximates inverse rank). The relevance of this distribution for music has been demonstrated for the cases of pitch and harmony.[49]

Zipf’s law relates in two ways to modeling as well as theoretical descriptions: On the one hand, it implies that fair models or descriptions may be achieved employing a small number of rules (capturing the rules governing the most frequent items). On the other hand, however, a complete or comprehensive description requires an exponential number of rules and exponential effort; the accurate completion of this is, without the aid of computational analysis, a virtually intractable task for human analytic scholarship and even with computational methods, a comprehensive description would hold little informational value. Therefore, the problems of overfitting, sparsity and Zipf’s law define crucial constraints for descriptions in music theory: Style descriptions (say of Handel’s suites, or a structure like sonata form in general) do not benefit from extensive and indefinite addition of detail and description —even if the Sisyphean task of a comprehensive description were tractable and possible for a particular repertoire in decades of analytical scholarship. This problem is further aggravated because the characterization of a musical style frequently deals with corpora that are historical and hence complete. Numerous music-theoretical approaches therefore operate in ways that are analogous to the case of ‘veridic’ modeling described above. Accordingly, such approaches face the problem of having to draw a careful line between meaningful description and generalization and problematic overfitting by adding excessive details that do not generalize and merely describe random artifacts and coincidences in the corpus—analogous to the case of veridical overfitting described above. The method of withholding a set of data that is not used for theory building and only for theory evaluation constitutes a core and obligatory standard in computational and statistical modeling[50], yet it is still almost entirely ignored in the standards of music-theoretical practice. Reflections on the nature of description, generalizability and model building may suggest the use of such standards of in future music-theoretical endeavors.

To conclude and to tap into the spirit of David Huron’s, Michael Cuthbert’s research paradigms (amongst others) as well as Ian Quinn’s reflection of musicology in the age of Big Data and Digital Humanities, music theoretical scholarship of the 21^st century may draw great benefit from close interdisciplinary collaboration and from taking on board a number of the issues raised above in theory building. In particular, this concerns aspects such as precise, formal definitions of concepts, operations, methods and notation, making explicit underlying assumptions, grounding theoretical concepts and their operationalization in firm psychological, cognitive, mathematical and computational foundations, defining testable hypotheses and evaluation criteria, and evaluating theoretically derived hypotheses that concern corpora or ways of listening in terms of computational or psychological research.[51]

4. Local and Hierarchical Structure

The discussion above has largely focused on only one specific type of expectancy models, namely local models (such as Markov or n-gram models, and to some extent, regular grammars) which share the common assumption that event prediction is only characterized by the local context, consisting of the immediately preceding events. However, a large number of music-theoretical models such as those proposed by Schenker or more the strictly formalized approaches of Alan Keiler, Fred Lerdahl and Ray Jackendoff (GTTM), Eugene Narmour, Mark Steedman, Martin Rohrmeier, and Jonah Katz and David Pesetsky[52], take as their basis hierarchical principles of musical structure, which formally exceed the expressive power of local models and postulate both proximate and distal realizations of implications.[53] With respect to music expectancy, however, nonlocal models come packed with a number of implications that are not self-evident, outlined below.

Hierarchical Structure and Expectancy

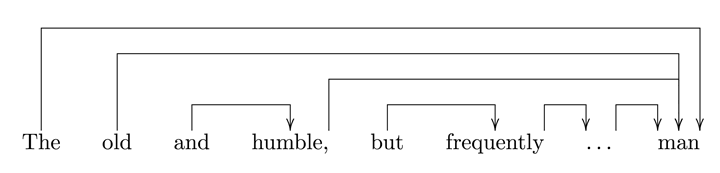
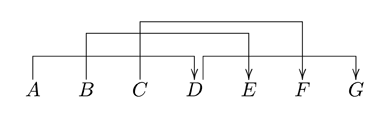
One linguistic example will first illustrate the issues involved in hierarchical processing before turning back to music. Speaking about a man, which word or word class is predicted by “the old…”? One might say: “man” or a noun. The continuation, however, is: “the old and…”. Was the prediction “man” violated or unfulfilled? What is the new prediction? Is it “humble” (or any adjective) or is it still “man”? In some sense, it is both. Continuing as “the old and humble…”, one may now be aware that the prediction may be “man” yet also “but”, for instance: “the old and humble, but…” or “the old and humble, but frequently… man” etc. A merely local account (i.e., an account that treats predictions as strictly local) is insufficient for such a case. For instance, arriving at “but frequently” a trigram model would have lost the context of “the …” predicting a noun and may, in contrast, predict the continuation “but frequently you [will]”. A complex expectancy structure like the one illustrated by the present example involves nonlocal dependencies and predictions that may be interrupted by another structure. This is illustrated by the dependency structure represented in Figure 5. This example illustrates that cases like this require an account that is able to capture such hierarchical, potentially nested dependencies, for instance, by employing representations of a flexible number of simultaneous instances of predictions at different local or nonlocal levels.

Figure 5. Nested syntactic patterns of expectancy

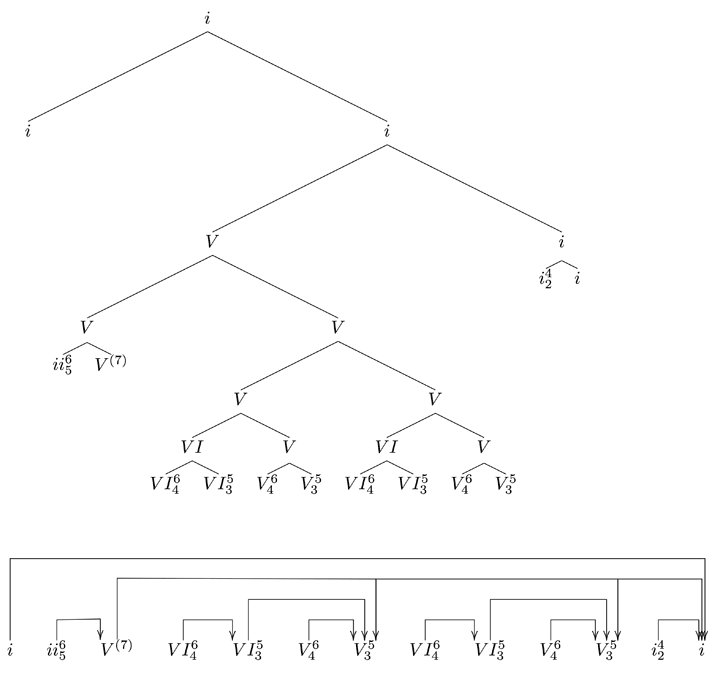
This case bears a musical analogue. Figure 6 illustrates several ways in which local and nonlocal types of expectancy are linked together. First, there are several local implications: ii^6/5 (m. 2) implying V (m. 3), V (mm. 3, 5, and 7) implying I, VI^6/4 implying VI^5/3 (m. 4), V^6/4 implying V^5/3 (m. 5), I^7/4/2 implying I (m. 8; note that this latter implication is context-dependent; in a neutral, non-cadential context the implication pattern would more likely be I^7/4/2–V^6/5). All of these local implications are immediately met except for the V–I implication, which is not (immediately!) met all three times. Note further that implication and realization pairs are tightly linked by the fact that realization events and new implicative events are combined: e.g., the V chord in m. 3, which is the expected realization of the ii^6/5 in m. 2, in turn sets up a new expectation. The expectation set up by the V chord (m. 3, 5) is violated twice by the same V–VI^6/4 deceptive progression (m. 4, 6; note that the second occurrence establishes a stronger implication due to the doubling of the bass note of V in m. 5). In turn the sequence VI^6/4–VI^5/3–V^6/4–V^5/3 constitutes a chain of mutual implication-realization patterns (combined with a 6–5–6–5 voice-leading pattern); this chain leads to the reestablishment of the V harmony and raises again the previously unfulfilled expectation of a I sonority, only to interrupt it once again – constituting a “one-more-time pattern.”[54] The third time, V proceeds to V⁷, demarcating the end of the eight-bar phrase, yet not resolving into I immediately despite the right bass note at m. 8. Accordingly, the final chord is locally implied by the V⁷ chord at the end of m. 7 while being interrupted by an even more local implication of the I^7/4/2. This constitutes a form of two nested implications. Moreover, the three V chords may be regarded at a higher level as a prolongation of an overarching V function that sets up a strong final V–I implication by virtue of being interrupted and reestablished twice by deceptive progressions, thus reinforcing a chain of implications towards the final V. In this respect the nested implications of the musical example are analogous to the linguistic example above. It is important not to neglect the fact that the first two chords establish the key of F minor almost unambiguously due to their scale membership[55] and thus strengthen the V–I expectation. Furthermore, the I chord may be analyzed as setting up an expectation itself in terms of its implied tonic return at the end of the period. Altogether this example motivates a representation of the different implication-realization patterns or nested expectancies as set up in the example of this sonata movement. Turning back to the linguistic example, the I and V chords set up nonlocal implications that are maintained and interrupted by several other patterns of implication and realization until they are realized.

Figure 6. Wolfgang Amadé Mozart, Piano Sonata F-Major, KV 280, second movement, mm. 1–8

Figure 7. Visualization of the nested patterns of expectancy in the Mozart phrase from Figure 6

Such hierarchically nested patterns of expectancy involve both local and nonlocal components.[56] Note that, for instance, in Figure 7 the arrows are organized in a way that some may be superordinate to two or more others.[57] Such a hierarchical form of organization entails a tree-based representation. This formalization of the hierarchical understanding of musical dependency and expectancy is useful for casting precise and testable predictions that may not be straightforward under an informal notion of hierarchicality. Specifically, it predicts that crossed patterns of implication-realization events such as those in Figure 8 may not occur.[58] As outlined before, the requirement for processing (and listening to) such a structure is the ability to keep more than one open implication actively in mind, while other intervening events and patterns of implication, realization, and prolongation occur.

Figure 8. Crossing patterns of expectancy that are predicted to be impossible in musical contexts

Once a hierarchical model of music is involved, the notion of expectancy becomes less straightforward (as outlined in the previous example). One cannot easily predict the next event any more because an interruption of a current implication may occur at a large number of points. Consequently, to say that a I–IV–V progression implies a I now entails the awareness that the implied I may occur several measures later after a potentially large series of multiple and recursive interruptions. Examples of such structures may be found in the analysis of deceptive cadences and half cadences amongst other phenomena.[59] In this context, a recent empirical study provides neural evidence that nonmusicians process original and modified versions of two two-part phrases from Bach’s chorales differently, depending on whether the second part returned to the initial key of the entire phrase or not after a (comparably long) intermitting modulation.[60] Such a case of nonlocal prediction provides a prototypical example of predictive processes that cannot parsimoniously be expressed by virtue of plain local, n-gram or Markov models and suggests that we possess and employ capacities of nonlocal processing in music, for the least supplementing local processing[61]).

Expectancy Violation and Revision in Hierarchical Models

The example above illustrates that the notions of expectancy fulfillment and expectancy violation need to be reconsidered when taking into account a hierarchical model of structural organization: Returning to the sentence “the old and humble, but frequently … man,” the occurrences of “but,” “and,” “old,” or “frequently” might further be regarded as instances of expectancy violation in the context of local predictions. Assuming that the ongoing listening/parsing process maintains an updated version of the best possible analysis[62], the time course of analyzing the sentence involves that, having expected the word “man” to close the noun phrase (NP), the parser is required to adapt the inferred tree model of the NP to accommodate for the newly encountered information. In terms of the predicted tree structure, encountering a less probable, yet grammatically correct option like “but” forces another adaption to the sentence model during online perception. This is an instance of an expectancy violation due to a less probable but grammatical event—a case contrasting the violation through an ungrammatical event such as “the old and but” where there is no structural recovery possible.

In addition, the nested dependency structure requires that all parts are fulfilled: “the old and man” strikes one as ungrammatical even though the nonlocal structural predictive dependency is fulfilled. An analogous musical example of this may be found in the following common-practice harmonic sequences:

(1*) I V ii^6/5 I

(2*) I V ii^6/5 V^6/4 I

In both cases, the two overarching implications are fulfilled, but the local contexts involve open implicative dependencies (ii^6/5 or V^6/4) that require closure for the sequence to be regular. An analogous example could be constructed for the respective nonlocal dependencies.

(3*) I […] ii V || vi iii vi V/iii iii

(4) I […] ii V || vi iii vi V I

Assuming that these two examples would occur constituting the context of a complete 8-measure period, their difference illustrates the style-specific necessity of the tonic return after a progression to V and particularly after a non-tonic continuation in the second half of the phrase in order to fulfill the nested predictive dependencies—just as illustrated by the empirical study mentioned in the previous paragraph.[63]

An understanding of expectancy in terms of hierarchical structure and multiple (recursively) nested predictive dependency relationships bears further consequences for the concept of expectancy violation: While expectancy and its violation is a mere matter of degrees of continuous probability values for a local model, patterns of expectancy receive a different interpretation in a hierarchical account. Common musical patterns such deceptive cadences, one-more time patterns, interruption, etc., may be accounted for in terms of overarching nonlocal dependencies. Accordingly, what may appear to a local model as a local expectancy violation, may resolve into a regular analysis under the perspective of a hierarchical account. In these terms, an expectancy violation may likely be a local interruption of an established predictive event, which delays or defers the realization of the predicted event and in turn sets up a new nested predictive context (analogous to “but frequently…” in the language example). A very simple example of this is provided by the following harmonic progression:

(5) I ii V [ vi ii V ] I

This sequence sets up a V–I implication which is interrupted by a deceptive progression V–vi which in turn initiates two further predictive dependencies to reestablish (and potentially strengthen) the predictive effect of the initial dominant context (as indicated by the brackets). In the tree analysis vi would not be merged with the preceding V, but analyzed as subordinated to ii and hence be merged with ii. This understanding may be useful to recast a variety of deceptive cadences in terms of recursively embedded predictive dependencies rather than understanding them solely in local terms of ‘regular’ and ‘less regular’ continuations of a dominant.[64]

Two Case Studies of Expectancy Violation and Revision

The hierarchical understanding of expectancy outlined above further entails a link between expectancy violation and revision. As argued above, the update of the current tree based on the previous context in an instance of Jackendoff’s idealized parser may require smaller or larger adaptations of the tree structure based on newly encountered unexpected events. Within the framework of a recursive grammar model such updates of the tree structure may imply further change and revision of previously heard structure.

Figure 9. Ludwig van Beethoven, Symphony I, C Major, op. 21, first movement, mm. 1–13

Two well-known examples illustrate this, the beginning of Ludwig van Beethoven’s First Symphony (Fig. 9) and the beginning of Robert Schumann’s lied “Am leuchtenden Sommermorgen” (Fig. 10).[65] The beginning of Beethoven’s symphony initially implies the key of F major by an unusual initial, dynamically reinforced dominant-seventh chord (m. 1). This tonal context is immediately revised to the key of C major by virtue of a deceptive progression (V–vi, m. 2). This weakly established C-major key is in turn revised by the subsequent seventh chord on D setting up a prediction for a (local) tonic G-major chord (m. 3). Finally this G-major context is functionally revised to be the dominant of the C-major key (mm. 4–7), which turns out to be underlying key of the entire passage. This passage can be interpreted in close analogy to linguistic ‘garden path’ phenomena such as “The horse raced past the barn fell” (which forces a parse of “The horse [(that) raced past the barn] fell” rather than “[The horse raced past the barn] fell”, which requires the parser to backtrack and revise the entire constituent structure after encountering the word “fell”). In analogy, the remarkable feature of this segment is that the expectancy violations trigger a reparse and revision of the underlying key and the entire set of assigned scale degrees and tonal functions three times for three different points of tonal reference.

A phenomenon like this suggests that the process of expectancy formation is a by-product of predictive generative parsing and that expectancy violations inform an internal update and revision process of the parser (the likely candidate parse(s) is/are generated on the fly and interactively matched with the incoming stream of events to update the best current candidate parse(s)). In his discussion of this phenomenon, Ray Jackendoff asserts a similar dynamic parsing process for rhythmic or metrical ambiguities.[66] Finally, it is important to note in this context that a mere plain local Markovian account of musical processing (as outlined above) is in principle incapable of capturing such features relating to a parsing process since it does by definition not incorporate a representation of underlying deep structure that may be revised on the fly.

Figure 10. Schumann, “Am leuchtenden Sommermorgen”, No. 12 from Dichterliebe, mm. 1–13

Schumann’s lied “Am leuchtenden Sommermorgen” illustrates an additional feature of expectancy formation, expectancy violation, and parsing by predictive processing. The opening of the piece creates a strong surprise by continuing what sounds like a dominant-seventh chord with a 6-4 suspension and a semitone descent in the bass. The strong effect is caused by the sudden effort required by the parsing process to revise the dominant-seventh tonic expectancy retrospectively towards an unlikely German sixth, a precedential V^6/4 progression in a different key (B vs. B^b). As in the previous example the parsing process is forced to reinterpret both tonal function and key structure. The formal preconditions of this strong effect are two-fold: Firstly, within the tonal system functionally ambiguous chords are possible and, secondly, the probabilities of the competing interpretations are skewed (i.e., they diverge largely[67]).

The example of Schumann’s lied provides an additional instance of the interaction between predictive processing, online learning and expectancy violation: When the initial sonority reappears for the third time (m. 8) after a strong stabilization of the Bb-major key, it is continued as a dominant-seventh chord (mm. 8–9) providing the B-major context that was originally expected. However, after having created a strong garden-path effect by subverting the established hearing of the initial dominant seventh chord, Schumann here demonstrates a second comparably strong effect by playing yet another trick on the established expectation: After two occurrences of the German sixth chord reinterpretation, the continuation to B major which was previously the most likely has now turned into an unlikely progression. The basis of this effect is again twofold: Firstly, it takes advantage of the established Bb-major context and the higher likelihood of interpreting the sonority as a German sixth chord in Bb-major rather than expecting a modulation. Secondly, there is an effect of online learning of this motivic sequence during the course of the first eight measures.[68] With respect to the first aspect, it is important to note that, without any additional context, the probability of tonal function and key of the pitch class set Gb/F#–Bb/A#–Db/C#–(Fb)/E is highly favoring the interpretation of a dominant-seventh chord, whereas this probability changes once a previous context in the key of Bb is established. Regarding this second aspect, Schumann’s piece provides a case of online learning (or what Darrell Conklin as well as Marcus Pearce and Geraint Wiggins refer to as “short-term model,”)[69] i.e., learning during the course of a piece. Another example of the strong effects of expectancy violations based on online learning is found in the second movement of Schubert’s piano sonata A major D. 959, in which the multiple repetition of the A–G# motive in F# minor is unexpectedly replaced by the step A–G in D major (mm. 189–190). While this effect can be simply accounted for in terms of online learning and a short-term model of pitch-class distribution or melodic-harmonic bigram structure, this and the previous example illustrate the strong contribution of online-learning to listening and the interaction of long-term and short-term knowledge to musical experience.

Effects of expectancy, expectancy violation, ambiguity, and revision continue to have an (albeit weaker) effect even over the course of multiple listening. Such effects and their emotional correlates that remain after multiple listening would be difficult to account for considering the ongoing implicit learning and, particularly, the learning of the veridical structure of a piece. One potential explanation that solves this dilemma is proposed by Ray Jackendoff: He suggests that the parser constitutes a separate module that is “‘informationally encapsulated’ from long-term memory of pieces”[70] and overrides veridical knowledge to some extent by operating independently on the musical input. Accordingly, the same backtracking and revision processes would still operate each time we listen to the opening of Beethoven’s first symphony triggering similar emotional effects despite our growing knowledge of the piece.

Altogether, the examples above illustrate how closely musical expectancy is linked to implicit learning and implicit knowledge both in long-term enculturation and short-term musical listening.[71] It is further deeply grounded in the processing of local as well as hierarchical structure, and involves multiple nested dependencies as well as the workings of the recursive parsing mechanism that provides incremental structure building, predictive generation, update and revision processes. Automatic expectancy formation, effects of retardation, anticipation, expectancy violations, deceptive structures, ambiguity, musical garden-path phenomena and revision: Such effects in musical listening and the emotional experience[72] result from the operation of an ongoing parsing mechanism that processes the musical stream, generates likely parses and continuations, and matches them with the ongoing stream of musical events.

5. Conclusion

Generally, perspectives of cognition and modeling may provide a number of contributions to the field of music theory: Apart from demonstrating the necessity of precise specification of covert assumptions and characterizing constraints of theoretical description that arise from problems such as sparsity or overfitting, they illustrate the insight that theoretical models of music and expectancy are intrinsically linked to implicit or explicit underlying formal, computational assumptions.

After all, musical expectancy is intrinsically linked to cognitive accounts of predictive processing. It provides a constructive case for the mutual interaction of music theory and music cognition[73] and illuminates ways in which concepts from music cognition, computational modeling, and (neuro)psychology may help to address music-theoretical issues from a different perspective. They provide ways to support, adapt, and revise music-theoretical concepts, to clarify theory formation in music analysis and to take into account music-theoretical insights in the formation of cognitive theory.