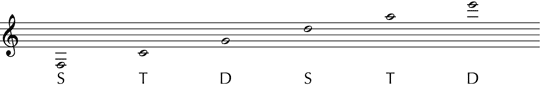Albert Simon – ein ungarischer Autor

Die ›Theorie der Tonfelder‹ des ungarischen Dirigenten und Musiktheoretikers Albert Simon wurde in den letzten Jahren in mehreren Aufsätzen erwähnt, kommentiert oder analytisch aufgegriffen.[1] Bekannt geworden ist die Theorie allerdings allein durch die Einführung von Bernhard Haas aus dem Jahre 2004, der sich auf persönliche Unterweisung durch Simon beruft.[2] Insbesondere fehlen uns bis heute Einblicke in eine Niederschrift Simons – ob eine vollständige Arbeit oder nur ein Manuskript vorliegt, ist nicht bekannt –, in der er offenbar die Summe seiner theoretischen Arbeiten festgehalten hat.[3] Trotz dieser Einschränkung, die Aussagen über Simons Theorie nur unter Vorbehalt möglich macht, sind die Wurzeln von Simons Denken in der ungarischen Musiktheorie offenkundig. Im Folgenden sollen Gemeinsamkeiten und Unterschiede zwischen Simons Theorie und den Theorien anderer ungarischer Musiktheoretiker herausgearbeitet werden.

Im Wesentlichen sind es drei Autoren, zu deren Schriften Simons Theorie einen engen Bezug aufweist: Lajos Bárdos mit seiner Darstellung modaler Harmoniefolgen bei Franz Liszt[4], Zsoltán Gárdonyi mit dem sogenannten ›Distanzprinzip‹ sowie Ernö Lendvai mit dem an Béla Bartóks Werken entwickelten Achsensystem.[5] Während Gárdonyi in wesentlichen Punkten an Bárdos anknüpft, muss Lendvais Systementwurf als eigenständig angesehen werden.[6]

Die Ansätze der drei Autoren werden zunächst vorgestellt und dann mit Simons Tonfeld-Theorie verglichen. Die Darstellung orientiert sich dabei nicht an chronologischen, sondern an inhaltlichen Aspekten: Im Blickpunkt stehen das Begriffspaar ›authentisch-plagal‹ sowie der jeweilige Umgang der Autoren mit der Riemannschen Funktionstheorie. Schließlich wird gezeigt, in welcher Weise bestimmte, bereits existierende Begriffe oder Phänomene[7] in die Tonfeldtheorie einbezogen werden.

A. Systeme vor Simon

1. Bárdos Neomodalität

Bárdos’ Aufsatz »Modale Harmonien in den Werken von Franz Liszt« geht von der Beobachtung aus, dass sich bestimmte harmonische Wendungen, die für die Klangsprache Franz Liszts charakteristisch sind, einer an der Klassik orientierten kadenzharmonischen Deutung entziehen. Solche Wendungen bezeichnet Bárdos als modal. Sein Modalitätsbegriff ist dabei weit gefasst und bezieht sich auch auf die Musik Palestrinas und seiner Zeitgenossen. Deren Kompositionsweise wiederum beschreibt Bárdos mit dem Begriff »harmonische Polyphonie«.[8] Auch dieser hat bei Bárdos einen stilübergreifenden Sinn: Bereits bei Palestrina sei der einzelne Klang nicht mehr bloß horizontal als ein Zusammentreten verschiedener Stimmen, sondern ›harmonisch‹ als Terzschichtung zu deuten. Ausgehend von diesem Palestrina-Verständnis versucht Bárdos zwischen ›funktioneller‹ und ›modaler‹ Harmonik zu unterscheiden.

Zur Beschreibung modaler Harmonik unterscheidet Bárdos zwischen der Anordnung von Akkorden im Sinne der Quintensäule auf der einen und der Terzensäule auf der anderen Seite. Mit Hilfe der Quintensäule misst Bárdos den Unterschied zwischen den Vorzeichen, die zwei Tonarten besitzen. So beträgt das Verhältnis C-Dur – D-Dur +2, das Verhältnis C-Dur – d-Moll -1. Den Unterschied in der absoluten Maßzahl (hier 2, dort 1) fasst Bárdos als Spannungsgrad zwischen den Tonika-Akkorden der jeweiligen Tonarten auf; zwischen einer Tonika C-Dur und einem D-Dur-Dreiklang ist der Spannungsgrad also größer als zwischen einem C-Dur- und einem d-Moll-Dreiklang.[9] Den Tonvorrat Palestrinas stellt Bárdos als Entwicklung in drei Schritten dar: siebenstufige Diatonie, gregorianische Achtstufigkeit (Erweiterung um das lydische b), modale Elfstufigkeit (Hinzunahme der drei erhöhten Stufen oder ›Diesen‹ cis, fis und gis).[10] Die Anordnung dieses Tonvorrats als Quintenreihe scheint in Bezug zum Prinzip der Quintensäule zu stehen.

Die Terzensäule umfasst im Gegensatz zur Quintensäule nur sieben Akkorde, da ihr Zweck die Beschreibung von Akkordrelationen innerhalb siebenstufiger Systeme ist. Bezogen auf einen Ausgangsakkord bezeichnet Bárdos Terzschritte abwärts als authentisch, aufwärts als plagal und definiert in jede Richtung ›Terzwendungen‹ von ein, zwei oder drei Terzen (Beispiel 1).[11]

Beispiel 1: Authentische und plagale Wendungen

Die Bestimmung einer Terzwendung geschieht unabhängig davon, ob die beteiligten Akkorde Dur- oder Moll-Akkorde sind und auf welcher Stufe einer Tonart sie stehen. Stehen zwei Akkorde im Tritonusabstand, spricht Bárdos von einer »polaren Wendung«.[12]

Entfernung/Spannungsgrad und das in Terzschritten beschriebene Wendungsverhältnis sind nicht als gegensätzliche Prinzipien, sondern als zwei unterschiedliche Qualitäten einer Akkordverbindung zu betrachten. So ist beispielsweise die Fortschreitung A-Dur - fis-Moll eine authentische Terzwendung, deren beide Akkorde sich auf denselben Tonikagrundton a beziehen, bei der Fortschreitung fis-Moll - e-Moll hingegen handelt es sich um eine plagale Wendung (drei Terzen aufwärts), die auf der Quintensäule einen Abstand von zwei Quinten hat.

Bárdos demonstriert seine Analysemethode an zahlreichen Beispielen, bei denen es sich meist um kurze Werkausschnitte handelt. Er unterscheidet zwischen modal-harmonischen Phänomenen, die mehr oder weniger an Palestrina anknüpfen, und solchen, die als Ergebnis einer Weiterentwicklung modaler Harmonik durch Franz Liszt zu betrachten sind. Die Zuordnung der Musikbeispiele zu einer der beiden Kategorien leuchtet in fast allen Fällen unmittelbar ein, und die Beschreibung der modalen Vorgänge, die Bárdos anbietet, ist immer hinreichend differenziert. Allerdings ist nicht in jedem Beispiel klar, ob die Akkordrelationen im Sinne der Terzen- oder der Quintensäule betrachtet werden. Der so entstehende Eindruck der Unübersichtlichkeit wird dadurch verstärkt, dass mit relativen Solmisationsilben, Stufenziffern und Akkordbezeichnungen drei verschiedene Bezeichnungssysteme nebeneinander zur Anwendung kommen.[13]

Letztlich zielt Bárdos’ Artikel eher auf die Vorstellung einer empirisch fundierten Analysemethode als auf die Entwicklung eines Systems. Dies erhellt sich aus der Beobachtung, dass Bárdos seine ›Analysewerkzeuge‹ zwar ausführlich vorstellt, aber nicht begründet. So wird zum Beispiel nicht erklärt, ob Bárdos’ Anordnung des Palestrina-Tonvorrats in Quinten, die offenbar quer steht zur Vorstellung skalenförmig angeordneter Modi, durch eine entsprechende Erscheinungsform dieses Tonvorrats bei Liszt motiviert ist. Ebenso bleibt offen, warum zweiquintige Wendungen in besonderer Weise typisch für eine modale Klanglichkeit sein sollen.

2. Das Distanzprinzip

Das ›Distanzprinzip‹ wurde von Zoltán Gárdonyi entwickelt und in zwei Arbeiten vorgestellt.[14] Von diesen aus fand es Eingang in die Harmonik Zsolt Gárdonyis und Hubert Nordhoffs, in der sich die vielleicht einfachste und deutlichste Erklärung findet:

Der Begriff Distanzprinzip stammt aus dem Bereich der Akustik und wurde in der Musikforschung auf solche Tonhöhenordnungen übertragen, die auf einer Aufteilung der Oktave in gleiche oder alternierende Abstände und in diesem Sinn auf Periodizität beruhen.[15]

Das Distanzprinzip setzt die Möglichkeit enharmonischer Verwechslung voraus. Diese habe sich – so Zoltán Gárdonyi – in der ersten Hälfte des 19. Jahrhunderts etabliert. Dabei sei dem Klavier eine bedeutende Rolle zugekommen, weil es »die tastenmäßige sowie klangliche Identität verschieden benannter und notierter enharmonischer Töne«[16] augen- und ohrenfällig mache.

Distanzielle Vorgänge führt Zoltán Gárdonyi auf gleichstufige Tonhöhenordnungen oder alternierende Modellskalen zurück. Unter gleichstufige Tonhöhenordnungen fallen die Ganztonleiter, der Kleinterzzirkel, der Großterzzirkel und die Halboktave (sie teilen die Oktave in jeweils gleiche Teile). Alternierende Modellskalen entstehen durch die Kombination von zwei gleichstufigen Tonhöhenordnungen gleichen Typs. So entsteht etwa aus der Kombination zweier Kleinterzzirkel das Modell 1+2 (alternierende Achtstufigkeit), aus der Kombination zweier Großterzzirkel das Modell 1+3 (alternierende Sechsstufigkeit) und aus der Kombination zweier Halboktaven das Modell 1+5 (Beispiel 2); die Zahlen geben jeweils Halbtonschritte an.

Beispiel 2: Modellskalen nach Zoltán Gárdonyi

Jede der Modellskalen kann von einem gegebenen Grundton aus auf zwei Arten gebildet werden: das Modell 1+2 als Modus 1+2 oder 2+1, das Modell 1+3 als Modus 1+3 oder 3+1 und das Modell 1+5 als Modus 1+5 oder 5+1 (der Begriff ›Modus‹ lässt an Messiaen denken, dessen 2. Modus dem Modell 1+2 entspricht). Die Modellskalen sind, um in Messiaens Sprachgebrauch zu bleiben, nur ›begrenzt transponierbar‹. So erlaubt das Modell 1+2 eine Transpositionsmöglichkeit, sein anderer ›Modus‹ 2+1 ebenfalls eine, so dass sich für dieses Modell insgesamt vier Variationsmöglichkeiten ergeben. Auf diese Weise ergeben sich aus dem Modell 1+3 sechs Varianten, aus dem Modell 1+5 sogar zwölf.[17]

Analog zur Unterscheidung in Gleichstufigkeit und Modellskalen gliedert Gárdonyi die analytische Betrachtung der Musikbeispiele in die Darstellung harmonischer Zirkel und melodischer Skalen. Um problematischen Beispielen gerecht zu werden, nimmt er gelegentlich unvollständige Zirkel an und spricht dann von ›Stufen‹. (z.B. Kleinterzstufen im Unterschied zu Kleinterzzirkeln). Meist zeigen die Beispiele sequenzielle Vorgänge, deren Tonvorrat und/oder Harmoniefortschreitung sich auf eine der oben besprochenen Skalen zurückführen lässt.

Die Darstellung der jeweiligen Sequenzen durch Gárdonyi ist überzeugend und imponiert durch ihre Detailgenauigkeit. Allerdings erscheint die Zuordnung einzelner Musikbeispiele nicht immer zwingend. Beispielsweise tritt im Gefolge einer Modellskala wie der alternierenden Achtstufigkeit (2+1 oder 1+2) oft auch ein harmonischer Kleinterzzirkel auf, so dass aus dem Notentext eigentlich nicht hervorgeht, warum im einen Fall die Melodik, im anderen die Harmonik im Vordergrund stehen soll. Ebenso sieht Zoltán Gárdonyi keinen funktionalen Unterschied zwischen einzelnen Tönen, wenn etwa ein als Struktur wirksamer verminderter Vierklang erst durch kolorierende Nebennoten zur alternierenden Achtstufigkeit ergänzt wird. Hier zeigt sich eine gewisse Indifferenz, die damit zusammenhängt, dass z.B. Kleinterzstufen, Kleinterzirkel und alternierende Achtstufigkeit eigentlich denselben Tonvorrat repräsentieren. Es scheint, als könnten Gárdonyis Unterscheidungen am konkreten Tonsatz nicht weiter begründet werden, weshalb sie Gefahr laufen, bisweilen willkürlich zu wirken.

3. Das Achsensystem Ernö Lendvais

Lendvais erstmals in dem Aufsatz »Einführung in die Formen- und Harmoniewelt Bartóks«[18] dargestelltes Achsensystem besteht aus drei Achsen, die er als Tonika-, Dominant- und Subdominantachse bezeichnet. Ausgehend von einer Tonika c können die beiden anderen Achsen von den traditionellen Grundtönen g (Dominante) und f (Subdominante) aus gedacht werden. Jede der drei Achsen umfasst vier Akkordgrundtöne im Kleinterzabstand. Ausgehend von einer Tonika c gehören der Tonika-Achse also die Akkorde mit der Grundtönen es/dis, fis/ges und a an, der Dominant-Achse die Akkorde mit den Grundtönen g, b/ais, des/cis und e und der Subdominant-Achse die Akkorde mit den Grundtönen f, as/gis, h und d. Akkorde, deren Grundtöne im Tritonusabstand stehen, bezeichnet Lendvai als Gegenpole. Sie bilden innerhalb einer Achse einen sogenannten ›Ast‹. Lendvai unterscheidet zwischen einem Haupt- und einem Nebenast; wiederum bezogen auf eine Tonika c besteht der Hauptast aus den Akkorden auf c und fis/ges, der Nebenast aus den Akkorden auf a und es/dis.[19]

Lendvai versucht, die historische Notwendigkeit des Achsensystems durch Ableitung aus vier traditionellen ›Anschauungsmodellen‹ zu belegen: aus Vorstellungen der traditionellen Harmonielehre, der distanziellen Oktavteilung, der Akustik und der allgemeinen Musikgeschichtsschreibung. Als Anschauungsmodell der traditionellen Harmonielehre fungiert der Quintenzirkel. Ordnet man die Akkorde, die im Quintstieg einander folgen, nacheinander den Funktionszeichen S, T und D zu (der nächste Akkord ist wieder S), dann entspricht die dadurch entstehende Zuordnung exakt derjenigen des Achsensystems (Beispiel 3).

Beispiel 3: Quintstieg als Funktionsfolge

Aus der distanziellen Teilung der Oktave (zur Erzielung ›tonal indifferenter Relationen‹[20]) in drei gleichgroße Intervalle gewinnt Lendvai die Grundtöne c, e und as, die er den drei Hauptfunktionen T, D und S zuordnet. Durch Hinzufügung der jeweiligen Gegenpole sowie durch weitere proportionale Teilungen erhält Lendvai die bekannten Kleinterzrelationen des Achsensystems.

Im Sinne einer auf akustische Verhältnisse gestützten Musiktheorie interpretiert Lendvai das Verhältnis der Grundtöne von Dominante und Tonika als Beziehung eines Obertons zu einem Grundton. Daraus leitet er ab, dass zu einer Tonika c nicht nur der Akkord auf g, sondern auch diejenigen auf e und b (fünfter und siebter Oberton) als dominantisch aufzufassen sind. Da die Verhältnisse T-S und S-D dem Verhältnis D-T entsprechen, bilden die Akkorde auf a und es/dis Teile der Tonika, und die Akkorde auf d und as/gis gehören zur Subdominante f. Um den noch fehlenden vierten Pol jeder Achse ableiten zu können, geht Lendvai vom neunten Oberton d aus, der zuvor als Teil der Subdominant-Achse definiert wurde. Da dieser Ton d wieder im Quintverhältnis zum Dominantgrundton g steht, setzt er nach dem oben beschriebenen Verfahren die Akkorde auf h und f in ein subdominantisches Verhältnis zu g. Mit h als Akkordgrundton ist die Subdominantachse vollständig. Auf diese Weise lassen sich auch die fehlenden Akkordgrundtöne cis (Dominantachse) und fis (Tonikaachse) ableiten.

In der Geschichte der Harmonik erblickt Lendvai eine klare Entwicklung: von der Klassischen Harmonik mit ihren Hauptfunktionen und den jeweiligen Mollparallelen als Vertretern (Lendvai spricht von ›Nebenklängen‹) hin zur romantischen Harmonik mit ihrer Erweiterung der Vertretungsmöglichkeiten durch ›obere‹ Parallelen (Parallelen bezogen auf die Mollvarianten der Hauptfunktionen). Die logische Weiterführung der Geschichte bestünde darin, zu den bereits etablierten Parallelen eine weitere Parallele zu konstruieren. Die durch die Parallelenbildungen initiierte Kleinterzfolge wird durch den neuen vierten Akkord zyklisch zu einem Kleinterzzirkel geschlossen.

Die aus Zoltán Gárdonyis Distanzprinzip als ›Modellskalen‹ bekannten Tonleitern erscheinen auch in Lendvais System. Sie werden dort allerdings nicht wie bei Gárdonyi als Addition von Halbtonschritten (1+2, 1+3, 1+5), sondern als periodische Folge von Proportionen (1:2, 1:3, 1:5) ausgedrückt. Die Proportion 1:2 definiert also das Prinzip für den Aufbau einer Skala, die der Modellskala 1+2 bei Gárdonyi entspricht. Der Unterschied zu Gárdonyi hängt damit zusammen, dass Lendvai das Bartóksche Formdenken insgesamt auf das Prinzip des goldenen Schnittes zurückführt. Die Proportionen des goldenen Schnittes lassen sich wiederum durch die Zahlen der Fibonacci-Reihe (2, 3, 5, 8, 13, 21 …) ausdrücken. Die Tatsache, dass im Nenner der Proportionen seiner ›Modelle‹ ausschließlich Fibonacci-Zahlen erscheinen, ist für Lendvai ein Beleg für die Konsistenz von Bartóks musikalischem Denken. Im Gegensatz zu Gárdonyi, dessen ›Modellskalen‹ empirisch hergeleitet werden, versteht Lendvai seine Modelle also als Ausdruck eines übergeordneten Prinzips.

Unter den drei genannten ›Modellen‹ nimmt das Modell 1:2 für Lendvai eine Vorrangstellung ein. Zum einen stellt das Modell die skalenförmige Anordnung der Töne einer Achse dar (Beispiel 4). Daher kann Lendvai die drei möglichen Erscheinungsformen des Modells den drei Achsen T, D und S zuordnen. Zum anderen kann Lendvai verschiedene für Bartók typische klangliche Erscheinungen auf dieses Modell zurückführen, indem er, vergleichbar mit Gárdonyi, die Zahlen der Fibonacci-Reihe als Anzahl von Halbtonschritten versteht. Dazu nimmt er einen achttönigen ›α-Akkord‹ an, der die Achsengrundtöne der D- und T-Achse als verminderte Vierklänge nebeneinanderstellt (Beispiel 4). Die von diesem α-Akkord abgeleiteten Varianten β, γ und δ repräsentieren für Lendvai typische Bártok-Klänge. Dass sich dieser α-Akkord durch Fibonacci-Zahlen ausdrücken lässt (3+3+3+2+3+3+3), belegt die Kohärenz des Systems. Dies gilt auch für den von Lendvai so bezeichneten ›Bartók-Akkord‹, den er ebenfalls als Fibonacci-Anordnung (3+5+3) deuten kann (Beispiel 4). Außerdem lässt sich das Modell 1:2 auch als Kombination zweier Modelle 1:5 deuten (Beispiel 4) – das letztere Modell ist also in ersterem enthalten, was für Lendvai ein weiteres Mal die Vorrangstellung des Modells 1:2 unterstreicht.

Beispiel 4: Typische Bartók-Klänge (nach Lendvai)

Die Notenbeispiele zeigen, dass Lendvai das Achsensystem überwiegend zur Beschreibung formaler Strukturen, die Modelle und die von ihnen abgeleiteten Erscheinungen hingegen zur Beschreibung von einzelnen Klängen oder Tonfolgen verwendet. Es fällt auf, dass nicht in jedem Fall überzeugend begründet wird, warum ein bestimmter Ton als Vertreter einer Achse fungieren soll, ein anderer hingegen nicht. In systematischer Hinsicht gelingt es Lendvai ebenso wenig wie Zoltán Gárdonyi, eine Hierarchie zwischen den von ihm beschriebenen Phänomenen herzustellen, beispielsweise zwischen Achsensystem, Modell 1:2 und α-Akkord.

4. Zur Problematik harmonielehreartiger Systeme

Mit bemerkenswerter Deutlichkeit zeigt sich an den Schriften der drei bisher besprochenen Autoren dieselbe Problematik: Das Verhältnis der ›Analysewerkzeuge‹ zueinander ist nicht eindeutig und kann auch nicht aus den impliziten Voraussetzungen der Analysen erschlossen werden. Bei Bárdos und Gárdonyi dürfte diese Problematik damit zusammenhängen, dass ihre Analysen in Denkweisen der traditionellen Harmonielehre, bei Bárdos eher in der Funktionstheorie, bei Gardony eher in der Stufen- bzw. Fundamentschritttheorie verwurzelt sind.[21] Ihre Ansätze schreiben das zentrale Problem jedweder Harmonielehre fort: Die reduktive Erklärung des musikalischen Zusammenhangs mit Hilfe allgemeiner, quasi ›a priorischer‹[22] Regeln vermag dem einzelnen Kunstwerk kaum gerecht zu werden.[23] Offenbar lässt sich dieses Problem auch durch die Ergänzung zusätzlicher Kriterien – und nicht anders ist beispielsweise Bárdos’ Differenzierung in funktionale und modale Klänge zu verstehen – nicht lösen. Es überträgt sich vielmehr auf die weiteren Bestandteile des jeweiligen Systems: Da bereits die Beziehung des Grundmaterials – gemeint ist in diesem Fall der einzelne Akkord – zum konkreten Tonsatz nicht eindeutig ist, kann auch die Frage, was zusätzliche Kriterien zur Beschreibung des musikalischen Zusammenhangs beitragen, nicht beantwortet werden. Ebenso fehlen deshalb Kriterien für das Zusammenspiel der einzelnen Theorieelemente. Die geradezu unvermeidbare Indifferenz ›normativer‹[24] Theorien zeigt sich in der Analyse als Unklarheit in der Deutung von Details des jeweiligen Tonsatzes.[25]

B. Die Tonfeldtheorie nach Albert Simon und Bernhard Haas

1. Ähnlichkeit

Die Ansätze von Lajos Bárdos, Zoltán Gárdonyi und Ernö Lendvai sollen nun mit der Tonfeldtheorie Simons verglichen werden, so weit sie uns durch Bernhard Haas bekannt ist. Simon geht von drei Tonfeldern aus: ›Konstrukt‹, ›Funktion‹ und ›Quintenreihe‹. Mit den Bezeichnungen ›Funktion‹ und ›Quintenreihe‹ knüpft Simon an bekannte Termini an: Der Begriff ›Funktion‹ verweist offensichtlich auf Riemann, und die Bezeichnung ›Quintenreihe‹ erinnert an Bárdos’ ›Quintensäule‹, aber auch im weiteren Sinne an den Quintenzirkel. Lediglich der Begriff ›Konstrukt‹ geht auf Simon selbst zurück. Auch für die Strukturen der Tonfelder finden sich unschwer Vorbilder bei den drei bisher besprochenen Autoren. So entspricht das Tonfeld ›Funktion‹ Zoltán Gárdonyis alternierender Achtstufigkeit und Lendvais distanzieller Oktavteilung 1:2, während der Aufbau und die Struktur des Tonfeldes ›Konstrukt‹ mit Gárdonyis alternierender Sechsstufigkeit bzw. Lendvais distanzieller Oktavteilung 1:3 gleichzusetzen ist. Unterschiede zeigen sich hingegen bei der Quintenreihe. Bei den bisher besprochenen Autoren erscheint die Quinte als Prinzip der Anordnung des Tonmaterials, ohne dass an den unterschiedlichen Anordnungen selbst wiederum Qualitäten beobachtet würden. Simon jedoch differenziert die (Klang-)Qualitäten der unterschiedlichen Quintenreihen nach der Anzahl der beteiligten Töne. Überdies gilt ihm als bemerkenswerte Eigenschaft bestimmter Quintenreihen, dass sie einander komplementär zur Zwölftönigkeit ergänzen können: so etwa das größte Quintenfeld, das Enneaton, mit dem kleinsten, dem Triton.

Das Tonfeld ›Funktion‹ weist weitere Gemeinsamkeiten mit dem Achsensystem Lendvais auf. Mit Lendvai teilt Simon nicht nur die Riemannsche Nomenklatur, sondern auch die Dreizahl der Erscheinungen: Wie es bei Lendvai drei Pole gibt, so gibt es bei Simon drei ›Funktionen‹. Auch das Begriffspaar ›authentisch-plagal‹ taucht bei Simon im Zusammenhang mit dem Tonfeld ›Funktion‹ auf, und es bezeichnet Verwandtes: Authentisch ist der Wechsel in eine quinttiefere ›Funktion‹, plagal derjenige in eine quinthöhere. Den Begriff der Polarität verwendet Simon nicht[26], jedoch denjenigen der Äquivalenz: Eine Funktion hat vier Grundtöne, nämlich die tiefen Töne der vier Quinten, in die sich der Tonvorrat gliedern lässt. Äquivalent sind die Grundtöne in dem Sinne, dass jeder von ihnen in gleicher Weise Grundton der Funktion ist[27] (es gibt also kein Verhältnis von Grundton und Vertreter wie in der Funktionstheorie).

Vor diesem Hintergrund stellt sich die Frage, in welcher Form Simons Tonfeldtheorie die ungarische Theorietradition, in der sie offenkundig wurzelt, weiterentwickelt, und welche Lösungen sie für die bereits angesprochenen Probleme bietet. Zwei Fragestellungen sollen dabei als Orientierung dienen: 1. Wie stellt Simon die Verhältnisse zwischen den Tonfeldern dar? 2. Wie geht Simon mit Problemen um, die sich in der Vergangenheit aus der Verquickung innovativer Ideen der ungarischen Musiktheorie mit Denkweisen traditioneller Harmonielehren ergeben haben?

2. Lösungen

Vereinfachung

Im Gegensatz zu den erwähnten anderen Autoren gelingt es Simon, seine Theorie auf geradezu elegante Weise zu vereinfachen, d.h. von überflüssigen Theoremen zu befreien, ohne die Möglichkeiten zur Darstellung komplexer Sachverhalte zu beschneiden. So verzichtet Simon bei der Vorstellung der drei Tonfelder etwa auf umständliche Herleitungen oder ergänzende Elemente wie die Terzwendung, an der Bárdos und Gárdonyi das Prinzip der authentischen oder plagalen Bewegung festgemacht hatten. Das Intervall der Terz findet dafür innerhalb des Systems als integraler Bestandteil der Tonfelder Funktion und Konstrukt seinen Platz. Das auf diese Weise freiwerdende Begriffspaar ›authentisch-plagal‹ bezeichnet bei Simon, wie oben gezeigt, das Verhältnis zwischen zwei ›Funktionen‹. Ebenso fällt auf, dass eine Reihe der von den anderen Autoren getroffenen Unterscheidungen bei Simon wegfällt. Am offensichtlichsten ist hier sicherlich das Fehlen des Modells 1:5, dessen Identität mit dem Tonvorrat des Modells 1:2 auch Lendvai bewusst gewesen ist. Hier ist Simon in systematischer Hinsicht konsequenter, insofern er den bereits von Lendvai artikulierten Gedanken der Vorrangstellung des Modells 1:2 zu Ende denkt und das Modell 1:5 suspendiert.

Ein weiteres Moment der Vereinfachung stellt der Wegfall der ›Modi‹ dar, die Gárdonyi als Unterscheidungsmerkmal seiner Modellskalen einführt. Offenbar ist für Simon der Unterschied zwischen einem Modus 1+2 und einem Modus 2+1 nicht wesentlich, da ja ein Modus 2+1, bezogen auf eine Tonika c, wieder einem Modus 1+2, bezogen auf eine Subdominante f, entspricht. Dies gilt ebenso für Gárdonyis Unterscheidung von Stufen, Zirkeln und Modellskalen, die in Simons System keine Rolle mehr spielt.

Die Unterschiede zwischen den Theoremen Simons und denjenigen der anderen ungarischen Autoren verweisen allesamt auf eine für die Tonfeldtheorie wesentliche Denkfigur: Es muss unterschieden werden zwischen dem Tonvorrat, der als Substrat dem jeweiligen Tonfeld zugrunde liegt, und der Gestalt, in der sich das Tonfeld im musikalischen Kunstwerk manifestiert. So ist Lendvais Modell 1:5 für Simon zunächst nur eine Möglichkeit, eine melodische Gestalt aus einem Tonfeld ›Funktion‹ herauszuschneiden. Ob sie in einer konkreten Komposition tatsächlich erscheint, ist eine empirische Frage. Damit erhebt sich die Frage, welche Kriterien ein Ereignis innerhalb eines musikalischen Kunstwerks als Ausdruck eines bestimmten Tonfeldes erlebbar machen.

Die Tonfelder Simons unterscheiden sich in einem wesentlichen Punkt von den Modellskalen Lendvais und Gárdonyis: Sie sind nicht in Gestalt eines bestimmten Tonvorrats definiert, sondern ein bestimmter Tonvorrat wird aufgrund bestimmter Eigenschaften als Ausdruck eines Tonfeldes interpretiert. Haas’ Beschreibung der verschiedenen Quintenreihen verdeutlicht das: So wird vom Triton gesagt, es sei »stabil«[28], vom Tetraton, es habe etwas »Fließendes«[29], das Heptaton habe den Charakter der »Vollständigkeit«[30] usw. Dasselbe lässt sich in Bezug auf die drei verschiedenen Arten der Tonfelder beobachten: Dem Tonfeld ›Funktion‹ wohne die »gleitende Kraft des Umdeutens«[31] inne, das Konstrukt beziehe Töne »hermetisch« aufeinander. Die Quintenreihe bringe einerseits nach und nach alle Töne und Intervalle hervor, andererseits verfüge sie nicht von vornherein über die Eigenschaft der Vollständigkeit, sondern habe latent das Ziel der Ergänzung zur Zwölftönigkeit.[32]

Die beschriebenen Eigenschaften eröffnen nun eine Perspektive zur Lösung des oben genannten Problems: War beispielsweise bei Lendvai die Frage, wann ein Ton einem bestimmten Pol angehört, nicht immer befriedigend zu lösen – vor allem gab es für Lendvai keine Möglichkeit einer Begründung –, so ist für die Tonfeldtheorie das Zustandekommen einer bestimmten Wirkung im musikalischen Kunstwerk das ausschlaggebende Kriterium. Die Begründung erfolgt dann auf der Basis von »Behauptungen […], die nur im jeweiligen Werk gelten«.[33]

Ausschließlichkeit

Ein bedeutender Unterschied zwischen Lendvai und Gárdonyi auf der einen Seite und Simon/Haas auf der anderen besteht darin, dass die Tonfelder als funktionale Einheiten verstanden werden und nicht als abstrakte Elemente, die innerhalb einer Komposition zur Anwendung kommen[34]:

Diese abstrakte Bestimmung ist noch nicht die Bestimmung der Wirkung bestimmter angebbarer Töne im Werk.[35]

Da sich der Sinn einer Tonfeldanalyse nur unmittelbar am Kunstwerk zeigen kann, verzichtet die Tonfeldtheorie auf eine ›wissenschaftliche‹ Begründung von der Art, dass die Realität von Phänomenen im Kunstwerk oder auch die Triftigkeit von Tonfeldern durch Herleitung aus an sich bestehenden Verhältnissen erwiesen wird. Umgekehrt beweist im Sinne der Tonfeldtheorie etwa das Gelingen der Ableitungen bei Lendvai nicht die Angemessenheit der Theorie für den musikalischen Zusammenhang. Man mag beispielsweise die Verhältnisse des goldenen Schnitts in der Komposition finden – den funktionalen Klangwirkungen gegenüber bleiben solche Beobachtungen äußerlich.[36]

Da Simon/Haas die Betrachtungen der Tonfelder nicht mehr mit Ansätzen der traditionellen Harmonielehre verbinden, vermeiden sie die Probleme, in die sich die eingangs besprochenen Autoren verstrickt hatten. Es ist schwer vorstellbar, wie ein Ansatz, der von der Erfahrung funktionaler Klangwirkungen ausgeht, mit einem traditionellen Ansatz vereinbar sein sollte, der Akkorde und Stufen als präexistente Grundelemente begreift: Im Kontext der Tonfeldtheorie »fällt der gewöhnliche Akkordbegriff; stets entscheidet nur der Zusammenhang des Werks, was auf welche Weise zusammengehört«.[37]

Im Gegensatz gerade zu Lendvai, der das Verhältnis der Grundtöne einer Achse noch als »Funktionsverwandtschaft von 4 verschiedenen, auf dem Grundriß des verminderten Vierklangs beruhenden Tonalitäten«[38] beschreibt, geht es der Tonfeldtheorie um die Wirkung einzelner ein Tonfeld konstituierender Töne im Werk.[39] Demnach sind auch Akkorde nur eine Möglichkeit, ein bestimmtes Tonfeld im Werk auszudrücken. Was in systematischer Hinsicht eine Vereinfachung darstellt, erweist sich bei der Analyse allerdings als spezielle Schwierigkeit: Die Frage, welcher Ton auf welcher Ebene des Tonsatzes ein Tonfeld repräsentiert, ist selten schnell und eindeutig zu lösen.

Die äußerst konzentriert wirkende Form der Tonfeldtheorie bei Haas ermöglicht einen ersten Blick auf die Beziehungen der Tonfelder zueinander, vor allem aber auf ihr Verhältnis zum Werk: Haas geht in seiner Einführung davon aus, dass das Ganze eines musikalischen Kunstwerks durch (meist) zwei Tonfelder ausgedrückt wird, den sogenannten ›Tonfeldern des Ganzen‹. Von diesen können dann gleichsam Schicht für Schicht die für das singuläre Kunstwerk charakteristischen Ereignisse abgeleitet werden. Haas Darstellung bietet also eine Lösung für das bei Bárdos und Gárdonyi noch ungeklärte Verhältnis der einzelnen ›Analysewerkzeuge‹. Darüber hinaus unterscheidet sich die Tonfeldtheorie gerade von Gárdonyis Ansatz durch die grundsätzliche Forderung Simons, jeden Ton eines Stückes zu erklären.[40]

2. Bedeutung der Analyse

Die Tonfeld-Theorie Simons unterscheidet sich von den Ansätzen der anderen hier behandelten ungarischen Autoren vor allem hinsichtlich der Bedeutung der Analyse innerhalb der Theorie.

Bárdos’ Aufsatz ist eine Spezialuntersuchung zur Modalität im Werk Franz Liszts, die auf harmonielehreartigen Prinzipien basiert. Diese thematische Beschränkung definiert die Bedeutung der Analysen: Sie dienen bei Bárdos dazu, das Werk Liszts im Hinblick auf modale Wendungen zu betrachten.[41]

In ähnlicher Weise hat die Analyse auch bei Zoltán Gárdonyi die Aufgabe, distanzielle Vorgänge in Kompositionen aufzuzeigen. Meist handelt es sich um Sequenzen aus Werken von Liszt und Chopin (dabei ist sich Gárdonyi der begrenzten Reichweite seiner Analysemethode durchaus bewusst[42]). Im Abschnitt ›Strukturzusammenhänge‹ fasst er das Distanzprinzips als eine historische Tatsache auf, indem er erläutert, wie durch distanzielle Vorgänge die auf den drei Hauptfunktionen basierende Dur-Moll-Tonalität ›aufgelockert‹ und ›umgewandelt‹ worden sei und wie die zunehmende Verwendung der Halboktave traditionelle Strukturen überflüssig gemacht habe.[43]

Das Ziel von Lendvai besteht darin, das der Musik Béla Bartóks zugrunde liegende Tonsystem darzustellen. Die Beschränkung auf einen einzigen Komponisten[44], wird durch den Anspruch kompensiert, »den Prozess der Schaffung seines Materials« nachvollziehen, und zwar »bis zu den Wurzeln der Musik«.[45] Dazu wird das Tonsystem Bartóks historisch eingeordnet, und zwar zwischen klassischer (funktionaler) Harmonielehre und dem von Lendvai so genannten ›Zwölftonsystem‹.[46] Der Zusammenhang mit beiden ›Systemen‹ ist für Lendvai durch das Gelingen der entsprechenden Ableitungen bewiesen. Trotz des Zusammenhangs muss nach Lendvai die Bartóksche Zwölfstufigkeit von Schönbergs Zwölftonmusik deutlich unterschieden werden: Erstere erscheint als logische Fortsetzung romantischer Harmonik und partizipiert noch an deren grundsätzlichen Gegebenheiten, während letzterer unterstellt wird, die Tonalität zu ›zertrümmern‹.[47] Angesichts solcher Überlegungen geht die Aufgabe der Analysen bei Lendvai weit darüber hinaus, die ›Anwendbarkeit‹ des Achsensystems auf die Musik Bartóks zu belegen. Der Unterschied zur Bedeutung der Analyse bei Albert Simon bleibt dennoch beträchtlich. Die Tatsache nämlich, dass Haas die Tonfeld-Analyse als eine Form der funktionalen Analyse begreift, hat zur Konsequenz, dass die Relevanz analytischer Einzelentscheidungen letztlich nur im Kontext einer vollständigen Werkanalyse glaubhaft gemacht werden kann (was nicht ausschließt, dass auch Analysen von Werkausschnitten instruktiv sein können).

Auf die Schwierigkeit, die Anteile von Haas und Simon an der Schrift Die neue Tonalität von Schubert bis Webern zu trennen, ist bereits hingewiesen worden.[48] Einige wenige Zuordnungen können dennoch getroffen werden. Bernhard Haas ist ein ausgewiesener Kenner der Schenker-Analyse. Wenn also in einer Analyse die Schenkersche mit der Simonschen Analysemethode verglichen wird, so darf man davon ausgehen, dass dabei Simons eigene Perspektive überschritten wird. Am deutlichsten wird das in der Analyse von Schuberts Lied Ihr Bild, die von einer Analyse Schenkers ausgeht und diese mit einer Tonfeld-Analyse kontrastiert. Ebenso enthält auch die Analyse von Francks Fantaisie A-Dur Elemente der Theorie Schenkers. Die Beobachtung, dass Züge im Sinne Schenkers bei Franck nur noch vordergründig in Erscheinung treten, ist bezeichnend für die historische Perspektive, die Haas in seiner Einführung eröffnet.[49] Haas deutet an, dass Simon auch Kompositionen von Purcell und Bach auf die Anwesenheit von Tonfeld-Effekten hin untersucht hat.[50] Wenn diese Aussage zutrifft, könnte sie als Indiz für ein unkritisches Verhältnis Simons zur historischen Dimension seiner Theorie angesehen werden. Bei Haas jedenfalls wird die Tonalität der Tonfelder als ein geschichtlich vorübergehendes Phänomen in eine allgemeine ›Geschichte der Tonalitäten‹ eingeordnet. Auf eine Epoche der Stimmführungstonalität im Sinne Schenkers folgt demnach eine Epoche der Tonfeld-Tonalität im Sinne Simons. Der Zeitraum zwischen 1730 und 1850 kann dabei als Übergangszeit betrachtet werden, in der beide ›Tonalitäten‹ gewissermaßen ›parallel‹ existieren.[51] Eine solche Perspektive geht freilich weit über die der erwähnten ungarischen Autoren hinaus.

C. Ausblick

In der jüngsten Vergangenheit nimmt das Interesse an den analytischen Möglichkeiten der Tonfeldtheorie offenbar zu. Das zeigt sich exemplarisch an zwei Veröffentlichungen, einer von Stefan Rohringer zur Tonalität in Schuberts Klaviertrio B-Dur und einer von Johannes Schild zum Wirken von Tonfeldern in Wagners Parsifal.[52] Beide Arbeiten versuchen, bekannte analytische Probleme mithilfe der Tonfeldtheorie zu lösen: Rohringer geht von der Problematik der Sonatenform bei Schubert aus, Schild beschäftigt sich mit dem Problem der Einheit des musikalischen Kunstwerks bei Richard Wagner. Auffällig ist, dass beide Arbeiten den Begriff der Tonalität in den Mittelpunkt stellen. So knüpft Rohringer an Haas’ Analyse von Schuberts Ihr Bild an und versucht, das Verhältnis der beiden Tonalitäten (nach Schenker und Simon) am konkreten Beispiel zu deuten. Schild hingegen setzt bei der seit Ernst Kurth so genannten ›Krise der romantischen Harmonik‹ an (die wohl weniger eine Krise des Komponierens als eine der Musiktheorie gewesen ist) und zeigt mit Hilfe der Tonfelder, dass die in der Vergangenheit konstatierte ›Formlosigkeit‹ der Musik Wagners in Wirklichkeit keine gewesen ist, sondern eine neue, auf Tonfeldern gegründete Art des musikalischen Zusammenhangs. Über solche aktuellen Arbeiten hinaus darf man natürlich auf die Veröffentlichung des erwähnten Manuskripts von Albert Simon gespannt sein, die neue Erkenntnisse zur Musik Béla Bartóks erwarten lässt. Ein weiteres interessantes Arbeitsfeld eröffnet zudem die Frage, wie sich die Tonfeldtheorie zu einem musiktheoretischen Denken verhält, das sich primär an historischen Quellen orientiert.