Die Zirkelsequenz in Mozarts Klaviersonaten
Rudolf Rasch
In diesem Beitrag wird für Quintfallsequenzen, die alle Stufen einer Tonart durchlaufen, der Terminus ›Quintfall-Zirkelsequenz‹ oder kurz ›Zirkelsequenz‹ vorgeschlagen. Steht die Tonika nicht am Anfang und Ende, sondern in der Mitte, lässt sich von einer ›verschobenen Zirkelsequenz‹ sprechen. In einem ersten Teil (»Zur Theorie der Zirkelsequenz«) werden die Grundstruktur des Modells, sein Ursprung in der Mehrstimmigkeit und die Varianten seiner Ausarbeitung dargestellt. So können im Zuge der Ausarbeitung Akkordumkehrungen, leitereigene und alterierte Akkorde, Dreiklänge und Septakkorde verwendet werden. Ein zweiter Teil untersucht das Vorkommen und die kompositorische Verwendung von Zirkelsequenzen in Mozarts Klaviersonaten. Dabei wird deutlich, dass Mozart kein kompositorisches Standardverfahren kennt: Die insgesamt sechzehn Zirkelsequenzen in Mozarts Klaviersonaten unterscheiden sich hinsichtlich Taktart, Stimmenzahl, Motivik sowie harmonischer und kontrapunktischer Ausgestaltung zum Teil erheblich. Doch lassen sich auch wiederkehrende Aspekte des Modellgebrauchs herausarbeiten. Charakteristisch ist beispielsweise die Verklammerung von Akkordprogressionen durch übergreifende Motive. Auch finden sich Zirkelsequenzen durchwegs in locker gefügten Partien, etwa im Anschluss an die Exposition eines Haupt- oder Seitenthemas oder in den Couplets von Rondosätzen. Sowohl die terminologische Erfassung der ›Zirkelsequenz‹ als auch Untersuchungen zu ihrem Gebrauch bei Mozart sind bislang Desiderat geblieben. Hier setzt der vorliegende Beitrag an.
Zirkelsequenzen im weiten Sinne werden hier definiert als sequentielle Fortschreitungen, die alle Stufen der Tonart in festgelegter Reihenfolge und (in aller Regel) unter Verwendung eines fixen rhythmischen Wiederholungsmusters durchmessen. Eine bestimmte Form ist die Quintfall-Sequenz I-IV-VII-III-VI-II-VI-II-V-I. In diesem Beitrag werde ich mich auf diese Sequenzform beschränken, die ich einfach Zirkelsequenz (im engeren Sinne) nennen werde. Derartige Sequenzen erscheinen in etwa der Hälfte der Klaviersonaten Mozarts, und zwar ausschließlich in den Ecksätzen. Sie zu untersuchen und zu beschreiben ist der Zweck dieses Beitrags.[1]
Zur Theorie der Zirkelsequenz
Bezeichnungsweisen
Eine Sequenz kann allgemein als melodische, harmonische oder polyphone Idee beschrieben werden, die »wiederholt […] auf verschiedenen Tonhöhen« gebraucht wird.[2] Als Beispiel einer so verstandenen Sequenz seien die folgenden Takte des Presto aus Mozarts Klaviersonate KV 310 angeführt:
Beispiel 1: W.A. Mozart, Klaviersonate a-Moll KV 310, III. Satz, T. 56–59
Der Ausschnitt zeigt eine Idee, die in den Takten 56–57 exponiert, dann wiederholt und in den Takten 58–59 eine große Sekunde aufwärts transponiert wird. Die wiederkehrende Idee einer Sequenz wird im Folgenden ihr Modul genannt. Im gegebenen Beispiel hat das Modul eine harmonische Innenbeziehung, die als V-I -Progression beschrieben werden kann. Das harmonische Verhältnis des zweiten Moduls zum ersten, die Transpositionsbeziehung, ist das einer steigenden Sekunde. Es gibt noch eine dritte harmonische Relation, nämlich die Grenzbeziehung zwischen beiden Modulen, die fallende Kleinterz D-H. Da der Kern der Struktur in der Transposition des Moduls besteht, können solche Sequenzen transponierende Sequenzen genannt werden. Die Transposition kann entweder ›tonal‹ sein (mit einander folgenden Darstellungen der Idee in einer einzigen Tonart), oder ›real‹ (mit einem neuen tonalen Zentrum in jeder neuen Darstellung). Das oben gegebene Beispiel ist ›real‹.
Die Zirkelsequenz kann modellhaft folgendermaßen dargestellt werden:
Beispiel 2: Zirkelsequenz in C-Dur mit Dreiklängen
Die Akkorde der Sequenz werden im Folgenden auf dreierlei Weise bezeichnet: mithilfe von Ordinalzahlen (über dem Diskantsystem), Tonbuchstaben und Stufenbezeichnungen (unter dem Basssystem). Die Stufenfolge der Akkorde ist bei allen Zirkelsequenzen dieselbe. Die ordinale Nummerierung der Akkorde ermöglicht es, zwischen ungeradzahligen (1, 3, 5, 7) und geradzahligen Akkorden einer Sequenz (2, 4, 6, 8) zu unterscheiden. In Beispiel 2 etwa ist zu erkennen, dass die ungeradzahligen Akkorde den Grundton in der Oberstimme wiederholen, während die geradzahligen Akkorde in Quintlage erscheinen. Geradzahlige und ungeradzahlige Akkorde erscheinen meist in unterschiedlicher Lage. In diesem Fall können unmittelbar aufeinander folgende Akkorde nicht mit denselben Motiven und Texturen ausgearbeitet werden.
Struktur
Die Zirkelsequenz umfasst in ihrer vollständigen Form acht Akkorde. In aller Regel werden jeweils zwei Akkorde zu einem Akkordpaar zusammengefasst. Jede Einheit aus zwei Akkorden ist analog zur vorangegangenen aufgebaut, setzt aber eine Sekunde tiefer an. Der harmonischen Wiederholungsstruktur pflegt eine rhythmisch-metrische zu entsprechen. In sich ist die Zirkelsequenz dreigeteilt: Sie beginnt mit der Fortschreitung I-IV, die wir den ›Kopf‹ nennen wollen. Die letzten drei Akkorde bilden eine reguläre II-V-I-Kadenz (deren Sequenzcharakter erst durch die vorangegangene harmonische Bewegung zur Gänze deutlich wird). Ihr gegenüber stehen die mittleren Akkorde der Sequenz (VII-III-VI). Dieses ›Mittelglied‹ entzieht sich einer kadenziellen Interpretation: Die dritte Stufe bleibt funktional mehrdeutig und der ›unharmonische‹ Fundamentschritt von der IV. zur VII. Stufe (übermäßige Quarte bzw. verminderte Quinte) ist sequenzieller Analogiebildung geschuldet. Zwar folgen der Kopf (I-IV) und die Verbindung zwischen Mittelglied und nachfolgenden Kadenzen (VI-II) einer kadenziellen Logik, doch erschließt sich diese erst aus dem Kontext des Ganzen.
In Moll hat die Zirkelsequenz folgende Form:
Beispiel 3: Zirkelsequenz in a-Moll mit Dreiklängen
Auf den Kopf I-IV folgt das ›Mittelglied‹. Die Fortschreitung VII-III entspricht einer V-I-Kadenz in C-Dur, der Paralleltonart. Eine Kadenz in der Grundtonart (VI-II-V-I) bildet den ›Abschluss‹.
Akkordformen
Die funktionellen Tendenzen, die der Zirkelsequenz mit Dreiklängen innewohnen, treten durch die Verwendung von Septakkorden stärker in den Vordergrund:
Beispiel 4: Zirkelsequenz in C-Dur mit Septakkorden
Die Zirkelsequenz in Dur enthält vier verschiedene Typen von Septakkorden: einen Dominantseptakkord (7), drei kleine Moll-Septakkorde (4, 5, 6), zwei große Dur-Septakkorde (1, 2) und einen halbverminderten Septakkord (3).
In Moll gewinnt die Zirkelsequenz mit Septakkorden folgende Erscheinung:
Beispiel 5: Zirkelsequenz in a-Moll mit Septakkorden
Auch diese Sequenz enthält vier verschiedene Akkordtypen: Zwei Dominantseptakkorde (3, 7), zwei kleine Septakkorde (1, 2), zwei große Septakkorde (4, 5) und einen verminderten Septakkord (6). Der Dominantseptakkord 3 verstärkt die interne Kadenz 3-4 zur Durparallele. Die Septimen werden jeweils durch die Terz des vorangehenden Akkords vorbereitet und in die Terz des folgenden Akkords aufgelöst. Indem die Auflösung einer Dissonanz zugleich die Vorbereitung der nächsten bedeutet, sind alle Akkorde eng miteinander verknüpft. Zwei lineare Vorhaltsketten prägen den Oberstimmensatz der Sequenz.
Beispiel 6: Zirkelsequenz in C-Dur mit Vorhaltsketten im Sopran und Alt
Der Sopran enthält eine Vorhaltskette, die über den Leitton zur Tonika führt; der Alt eine weitere, die über die Dominantseptime in der Terz der Tonika endet; die Quinte fehlt im Schlussakkord. Tritt in der fünfstimmigen Formulierung eine zweite Altstimme hinzu, so wird ein vollständiger Schlussakkord erreicht.
Beispiel 7: Fünfstimmige Zirkelsequenz in C-Dur mit Vorhalten
Wichtige Varianten zum Grundmodell der Zirkelsequenz können durch Alterationen gebildet werden, die Zwischendominant-Septakkorde oder verminderte Septakkorde entstehen lassen. Zwischendominant-Septakkorde werden gebildet durch Verwendung einer Großterz statt Kleinterz in einem Moll-Septakkord (möglich in Akkord 4, 5 und 6 der Dursequenz und Akkord 1 und 2 der Mollsequenz) oder einer kleinen Septime statt der großen in einem Dur-Septakkord (möglich in Akkord 1 der Dursequenz und Akkord 4 der Mollsequenz). Weiterhin können Zwischendominanten zu Septnonenakkorden oder verminderten Akkorden transformiert werden. Verminderte Septakkorde lassen sich durch Alteration bilden, wobei der tiefste Ton des verminderten Septakkordes (zum Beispiel cis in cis-e-g-b) zumeist eine Großterz über dem Grundton des Sequenzakkordes (a in diesem Beispiel) steht.
Maximal können fünf Zwischendominanten verwendet werden, wie die nachfolgenden Beispiele (in C-Dur und a-Moll) zeigen. Ausgenommen sind lediglich die Klänge vor den Tritonusschritten (Dur: IV. Stufe, Moll: VI. Stufe):
Beispiel 8: Zirkelsequenz in C-Dur mit Zwischendominanten[3]
Beispiel 9: Zirkelsequenz in a-Moll mit Zwischendominanten
In der musikalischen Praxis ist eine solche Häufung von Zwischendominanten freilich selten, und einige der Akkordfolgen in den oben modellhaft skizzierten Beispielen sind ungebräuchlich.
Eine Zirkelsequenz enthält in der Regel eine oder mehrere transponierte Wiederholungen eines Moduls aus zwei Akkorden. Bezüglich der Zirkelsequenz ist der Begriff des Sequenzmoduls jedoch zweideutig. Das Modul kann definiert werden als die Folge der Akkorde 1-2 und wird dann wiederholt als 3-4, 5-6 und 7-8. Eine alternative Definition jedoch könnte auch die Akkordfolge 2-3 als Modul auffassen, die Akkordfolgen 4-5 und 6-7 als Wiederholungen sowie 1 und 8 als Halbmodule. Mitunter sind beide Definitionen gleichermaßen sinnvoll, da die Überschneidung von Phrasen und Motiven in der kompositorischen Ausarbeitung die Absetzung von Modulen verschleiern kann.
Stimmführung
Die Beschreibung der Zirkelsequenz als Akkordfortschreitung oder Stufenfolge könnte den Eindruck erwecken, es handle sich um ein primär harmonisches Modell. Unter Berücksichtigung ihres Ursprungs in der Musik des siebzehnten Jahrhunderts kann sie jedoch ebenso gut als eine mehrstimmige Struktur beschrieben werden, als ein Zusammengehen von vier melodischen Linien. Der Stimmverlauf im folgenden Beispiel ist derart gewählt, dass sich am Ende des Soprans eine ›clausula-cantizans‹-Formel zeigt, am Ende des Alts eine ›clausula altizans‹, des Tenors eine ›clausula tenorizans‹ und des Basses eine ›clausula basizans‹.
Beispiel 10: Zirkelsequenz in C-Dur als vierstimmiger mehrstimmiger Satz[4]
Es gibt verschiedene Möglichkeiten, eine Zirkelsequenz vierstimmig zu setzen. Eine glattere Form lässt sich durch Austausch der Tenor- und Bassnoten bei den geradzahligen Akkorden herstellen. Das Ergebnis ist ein Wechsel von Grund- und Sextakkorden.
Beispiel 11: Zirkelsequenz in C-Dur, vierstimmig, mit geradzahligen Akkorden in erster Umkehrung
Alt und Tenor verlaufen in fallenden Sekunden, Sopran und Bass im Wechsel von steigenden Sekunden und fallenden Terzen. Bei schematischer Beibehaltung des Stimmführungsmusters würde ein terzloser Schlussakkord erreicht. Es wäre möglich, die Terz in die Tenorstimme zu legen oder aber den Satz durch eine zweite Altstimme zur Fünfstimmigkeit zu ergänzen:
Beispiel 12: Fünfstimmige Zirkelsequenz in C-Dur
Die in den Beispielen 2–12 gezeigten Sequenzen sind ›Modelle‹ oder (im Sinne Schenkers) ›Mittelgrundstrukturen‹. In der musikalischen Wirklichkeit begegnen sie in vielfältig ausgearbeiteter Form.
Exkurs: Die Zirkelsequenz im musiktheoretischen Schrifttum seit 1900
Ungeachtet der großen Verbreitung jeglicher Art von Sequenzen im musikalischen Repertoire ist das einschlägige Schrifttum recht knapp bemessen. Natürlich widmet jede Harmonielehre einige Seiten Sequenzen verschiedener Art, und jedes große Musiklexikon hat einen Artikel zur ›Sequenz‹ (im hier gemeinten Sinne).[5] Offensichtlich aber gibt es bislang keine allgemein akzeptierte Art, Sequenzen zu klassifizieren. Die benutzten Termini sind uneinheitlich, und das Repertoire besprochener Sequenzen variiert stark. Spezialliteratur zur Sequenz ist rar.[6] Eine umfassende Darstellung, die auch systematischen Ansprüchen genügt, fehlt bis heute.
Das New Grove Dictionary (2001) widmet der Sequenz im Sinne eines wiederholten Moduls einen nicht mehr als siebzehnzeiligen Artikel.[7] Der aus der Ausgabe von 1980[8] identisch übernommene Text differenziert nicht zwischen verschiedenen Sequenztypen. Zwei kurze Musikbeispiele (von Beethoven und Chopin) stellen Zirkelsequenzen dar, ohne dass dieser Sonderaspekt zur Sprache käme. Das Stichwort »Sequence« im Sinne einer Gattung des gregorianischen Gesangs hingegen wird mit einem Artikel von fünfzehn Seiten, vielen ausführlichen Musikbeispielen und Hunderten von Literaturhinweisen bedient.[9] In Die Musik in Geschichte und Gegenwart (21998) wird die Sequenz mit einem Artikel von zweieinhalb Spalten Länge etwas ausführlicher dargestellt.[10] Der größere Teil des Textes widmet sich terminologischen Unterschieden, die jedoch nicht an Notenbeispielen erläutert sind, so dass unklar bleibt, ob die Zirkelsequenz mitgemeint ist oder nicht. Bemerkenswert ist der Schlusssatz des Artikels: »Um 1600 ist das Prinzip der Sequenz praktisch erschlossen und als Element der kompositorischen Gestaltung bis in die Gegenwart allgegenwärtig.« Der jüngste Literaturhinweis stammt aus dem Jahr 1836. Auch hier ist der Artikel über die gleichnamige Gattung des gregorianischen Gesangs um ein Mehrfaches länger.[11]
Musiktheoretische Lehrbücher behandeln die Sequenz in der Regel als einen Aspekt der Harmonik. Rudolf Louis und Ludwig Thuille beispielsweise diskutieren die Zirkelsequenz in ihrer Harmonielehre (1908) im Zuge der Besprechung von Nebenakkorden.[12] Analytische Beispiele in Dur und äolischem Moll sind beigefügt.[13] Die Zirkelsequenz wird umschrieben als eine »Sequenz von Dreiklängen oder Septakkorden mit quintweise fallendem (bzw. quartweise steigendem) Grundton«.
Ernest W. Mulder bespricht in seiner Harmonie Teil I (1947) die Zirkelsequenz als ein Beispiel für die Verwendung von Septakkorden in einer »Sequenz«, jedoch ohne Bezug auf Literaturbeispiele und ohne weitere terminologische Präzisierung.[14]
Allen Forte widmet der Zirkelsequenz (»circular progression by sequence«) eine Seite seiner Publikation Tonal Harmony in Concept and Practice (1962).[15] An anderer Stelle desselben Buches bespricht Forte auch die Variante mit Septakkorden.[16]
Walter Pistons Harmony (1976) ist vermutlich die erste Harmonielehre, die ein ganzes Kapitel allein der Sequenz widmet. Der größte Teil des Textes befasst sich freilich mit der transponierenden Sequenz.[17] Die Zirkelsequenz wird nur beiläufig erwähnt und durch ein Beispiel aus einer Klaviersonate von Dominico Paradies.
Carl Dahlhaus bezeichnet die Zirkelsequenz in seinen Untersuchungen über die Entstehung der harmonischen Tonalität (1967) als »geschlossene Sequenz«, deren zentrales Merkmal die Rückkehr zur Tonika sei.[18] In der Praxis, Sequenzen tonikal zu schließen, spiegele sich die im siebzehnten Jahrhundert neu entstehende harmonische Tonalität. Die Zirkelsequenz gehört für Dahlhaus zu einer größeren Klasse von Sequenzen mit fallenden Quinten (»Quintschrittsequenzen«), zusammen mit anderen Typen wie der modulierenden Sequenz (bei der die fallenden Quinten eine Modulation bewirken) und der »offenen Sequenz« (bei der die fallenden Quinten kein tonales Zentrum definieren).[19]
Edward Aldwells und Carl Schachters Harmony and Voice Leading (1978) enthält ein Kapitel über »Diatonic Sequences«, worin vier Sequenzkategorien besprochen werden: Sequenzen mit fallenden Quinten, mit steigenden Quinten, mit steigender 5-6-Technik und mit fallenden Terzen.[20] Der erste Typus entspricht dem, was hier Zirkelsequenz genannt wird. Beispiele aus Werken Händels und Mozarts sind angefügt.[21] Sequenzen werden außerdem im Zusammenhang mit Zwischendominanten behandelt.[22] Alles in allem schenken Aldwell und Schachter der Sequenz in der Mannigfaltigkeit ihrer Formen die gebotene Aufmerksamkeit.[23]
William Caplin trennt in Classical Form (1998) zwischen Kadenzfortschreitungen und Sequenzfortschreitungen.[24] Er unterscheidet sechs Sequenztypen, die sämtlich als Zirkelfolgen beschrieben sind, nämlich als Akkordfortschreitungen, die mit der Tonika beginnen und enden: »Quintfall« (unsere Zirkelsequenz), »Quintstieg« (I-V-II-VI-III-VII-IV-I), »Terzfall« (I-VI-IV-II-VII-V-III-I), »Terzstieg« (I-III-V-VII-II-IV-VII-I), »Sekundfall« (I-VII-VI-V-IV-III-II-I) und »Sekundstieg« (I-II-III-IV-V-VI-VII-I). Alle sechs Typen werden durch vierstimmige Notenbeispiele illustriert. Allerdings behandelt Caplin im analytischen Hauptteil seines Buchs lediglich vollständige Quintfallsequenzen. Die anderen Typen bleiben Theorie, wenigstens in ihrer vollständigen Form (obwohl sich Beispiele für Sekundfall-Sequenzen angeboten hätten). Caplin sichtet und bespricht viele Beispiele in den Werken Haydns, Mozarts und Beethovens, doch, von einigen zirkelförmigen Quintfallsequenzen abgesehen, bestehen diese nur aus einfachen Wiederholungen der ursprünglichen Idee, repräsentieren also das, was oben transponierende Sequenz genannt wurde. Die zitierten Sequenzen durchlaufen unterschiedlich viele harmonische Stufen, meistens zwei oder drei. Dadurch wird der Bezug zu den sechs zirkelförmig ausgearbeiteten Grundtypen problematisch, und Caplin analysiert diese transponierenden Sequenzen tatsächlich ohne Bezug auf die Zirkelformen. Stattdessen bezeichnet er das erste Auftreten der wiederholten Idee als »Modell«, seine Wiederholung als »Sequenz« und die transponierende Sequenz im Ganzen als »Modell-Sequenz-Technik«. Dadurch weicht Caplins Gebrauch des Terminus’ ›Sequenz‹ vom allgemeinen Usus ab, demzufolge unter Sequenz alle Erscheinungen der wiederholten Idee und nicht nur die zweite sowie die ihr folgenden zu verstehen sind. Caplin verwendet den Terminus Sequenzfortschreitung (»sequential progression«) auch, um transponierende Sequenzen zu beschreiben.
Die Zirkelsequenz spielt auch in Richard Taruskins Oxford History of Western Music (2005) eine Rolle.[25] Nach Taruskins Auffassung – wie zuvor bei Dahlhaus – gibt es einen engen Zusammenhang zwischen der Verwendung der Zirkelsequenz (die Taruskin den »diatonischen Quintenzirkel« nennt) in der italienischen Musik des ausgehenden siebzehnten Jahrhunderts und dem Aufstieg der harmonischen Tonalität zur selben Zeit. In Taruskins Worten: »When the diatonic circle of fifths became the basis of harmonic practice, the major-minor tonal system (or ›key system‹) can be said to have achieved its full elaboration.«[26] Es ist zu bezweifeln, dass die Zirkelsequenz die Grundlage der harmonischen Tonalität bildet – Kadenzfortschreitungen haben in dieser Hinsicht eine wichtigere Rolle gespielt. Sicher ist jedoch, dass die Verwendung von Zirkelsequenzen zu dieser Zeit beginnt. Das früheste Beispiel Taruskins entstammt Alessandro Scarlattis Oper Aldimiro (1683). Eine Durchsicht von Corellis Sonata a tre […] Opera prima (1681) hätte ebenfalls Beispiele geliefert.[27]
Die Zirkelsequenz in Mozarts Klaviersonaten
In neun der achtzehn Klaviersonaten Mozarts können insgesamt sechzehn Zirkelsequenzen nachgewiesen werden. Chronologisch sind die Sequenzen über das gesamte Corpus verbreitet, von der zweiten Sonate (KV 280) bis zur letzten (KV 576). Meist findet sich innerhalb einer Sonate nur eine Zirkelsequenz; die Sonaten KV 332, KV 545 und KV 570 enthalten jeweils zwei, die a-Moll Sonate KV 310 vier. Die folgende, chronologisch nummerierte Übersicht dient zugleich allen weiteren Verweisen als Legende.
Nr. 1: Sonate F-Dur KV 280, I. Satz, T. 18–22.
Nr. 2: Sonate B-Dur KV 281, I. Satz, T. 22–26.
Nr. 3: Sonate a-Moll KV 310, I. Satz, T. 5–8.
Nr. 4: Sonate a-Moll KV 310, I. Satz, T. 58–61, 62–65, 66–69.
Nr. 5: Sonate a-Moll KV 310, I. Satz, T. 70–73.
Nr. 6: Sonate a-Moll KV 310, III. Satz, T. 88–95.
Nr. 7: Sonate D-Dur KV 311, III. Satz, T. 133–136.
Nr. 8: Sonate F-Dur KV 332, I. Satz, T. 60–65.
Nr. 9: Sonate F-Dur KV 332, III. Satz, T. 46–48.
Nr. 10: Sonate B-Dur KV 333, I. Satz, T. 143–146.
Nr. 11: Sonate B-Dur KV 333, III. Satz, T. 189–193.
Nr. 12: Sonate C-Dur KV 545, I. Satz, T. 18–21.
Nr. 13: Sonate C-Dur KV 545, I. Satz, T. 37–40.
Nr. 14: Sonate B-Dur KV 570, I. Satz, T. 117–123.
Nr. 15: Sonate B-Dur KV 570, III. Satz, T. 59.
Nr. 16: Sonate B-Dur KV 576, III. Satz, T. 46–48.
Im Folgenden sollen diese Zirkelsequenzen unter verschiedenen Aspekten untersucht werden: Ausarbeitung und Textur, Akkorde und Module, Mehrstimmigkeit, Vollständigkeit etc. Abschließend wird ihre formale Einbettung im Kontext des jeweiligen Werkes beleuchtet.
Satzformen. Grundsätzlich tauchen Zirkelsequenzen nur in den schnellen Sätzen von Mozarts Klaviersonaten auf, bevorzugt bei Kopfsätzen in Sonatenhauptsatzform. Nur eine Sequenz begegnet in einem Schlusssatz in Sonatenhauptsatzform (KV 332: Nr. 9); drei finden sich in Schlusssätzen in Rondoform (Nr. 6: KV 310, Nr. 7: KV 311, Nr. 16: KV 576) und eine (Nr. 15: KV 570) in einem Schlusssatz ohne eindeutig klassifizierbare Form.
Taktarten. Die Sequenzen erscheinen in den verschiedensten Taktarten. Mit acht von sechzehn Beispielen ist der 4/4-Takt der häufigste. Der Akkordwechsel folgt fast immer mit einer Häufigkeit von zwei Akkorden pro Takt (Nr. 3–5 und 11–13) oder einem Akkord pro Takt im 2/4-Takt (Nr. 2, 6). Die Sequenz im dritten Satz von Sonate KV 576 (Nr. 16) zeigt vier Akkorde pro 2/4-Takt, also einen Akkordwechsel in Achteln. Gleiches gilt für die Sequenz im dritten Satz der Sonate KV 570 (Nr. 15), wo der gesamte Durchlauf aller acht Akkorde nur einen Takt beansprucht.
Ein 3/4-Takt kann entweder einen Sequenzakkord (Nr. 8) oder zwei enthalten (Nr. 14 und 1), ein 6/8-Takt entweder zwei Akkorde (Nr. 9) oder vier (Nr. 7). Die üblichste Lösung ist, dem ersten Akkord zwei Achtel, dem zweiten ein Achtel zuzumessen, wie in der Sequenz Nr. 7 beispielhaft durchgeführt. Die Sequenz Nr. 1 zeigt das komplementäre Verfahren mit einem Schlag für den ersten Akkord und zwei Schlägen für den zweiten. Es ist bemerkenswert, dass die Sequenz im ersten Satz der Sonate KV 332 (Nr. 8) mit einer Art von harmonischem accelerando endet: Nach mehreren Takten mit jeweils nur einem Akkord sind die letzten drei Akkorde (VI-II-V) hemiolisch rhythmisiert, mit drei Akkorden in zwei Takten. Die Sequenz im dritten Satz derselben Sonate (Nr. 9) enthält ebenfalls eine Beschleunigung am Ende, mit zwei Akkorden pro Halbtakt statt einem.[28]
Texturen. Schon ein flüchtiger Blick genügt, um zu erkennen, dass die Ausarbeitung der Sequenzen in satztechnischer Hinsicht außerordentlich vielfältig ist. Mehrere Zirkelsequenzen sind in Achtelnoten ausfiguriert (Nr. 8, 10, 11, 14, 15), eine in Achteltriolen (Nr. 1), einige in Sechzehntelnoten (Nr. 4, 5, 9, 12, 13), eine in Sechzehnteltriolen (Nr. 16) und eine in Zweiunddreißigstelnoten (Nr. 2). Meistens gibt es einen kleinsten Notenwert, der die Sequenz durchgehend strukturiert. Die Sequenz Nr. 3 bewegt sich in Achtel und Viertelnoten; ein ›Contre-temps‹-Rhythmus ist zu finden in den Sequenzen Nr. 8 und 11.
Figurale Varianten umfassen gebrochene und ungebrochene Akkorde, Tonleiterfiguren (steigend und fallend), Tonwiederholungen, diatonische Figuren, Oktavverdopplungen und Pausen zwischen einzelnen Noten. Auch die satztechnische Erscheinung ist sehr unterschiedlich. Zweistimmigkeit (mit einer Stimme pro Hand) ist am häufigsten (Nr. 1, 2, 7, 9, 12, 13, 15); Dreistimmigkeit (Nr. 5, 6, 8, 16) und Vierstimmigkeit (Nr. 4, 10, 11, 14) sind jeweils etwas seltener. Akkordsatz begegnet in den Sequenzen Nr. 3 und 10 (linke Hand) sowie Nr. 11 (rechte Hand). Die Satzweise der rechten Hand in den Sequenzen Nr. 3 (T. 6–7) und 8 kann auch als zweistimmige Mehrstimmigkeit gelesen werden, ebenso wie die ›gebrochenen Intervalle‹ der Sequenzen Nr. 7 und 10.
Motive. Die Verwendung von Motiven in Zirkelsequenzen weicht beträchtlich ab von jener in transponierenden Sequenzen. Bei letzteren ist ein Motiveinsatz in der Regel mit dem Sequenzmodul abgeschlossen, so dass Motiv und Modul zusammenfallen. In Zirkelsequenzen hingegen ist es die Regel, dass Motiveinsätze die Modulgrenzen übergreifen. Bei Mozart finden sich vor allem zwei Verfahrensweisen. Die erste zeigt zwei alternierende Motive, eines für die geradzahligen Akkorde der Sequenz und eines für die ungeradzahligen. Die Motive beginnen stets auf dem schwachen Taktteil eines Akkordes und enden auf dem starken Taktteil des nächsten Akkords. Es handelt sich also um akkordübergreifende Motive, die wir ›gerades‹ und ›ungerades‹ Motiv nennen wollen. Sie treten meist nur in der rechten Hand auf, während die linke Hand entweder Akkorde oder zumindest eine Textur hinzufügt, die dem metrischen Schema des Akkordwechsels entspricht. Hierdurch überlappen sich Motive in der rechten und linken Hand, was zu einem durchgängigen Bewegungsverlauf beiträgt. Deutlich zu erkennen ist dieses Verfahren in der Sequenz Nr. 9:
Beispiel 13: ›Gerade‹ und ›ungerade‹ Motive in Sequenz Nr. 9; W.A. Mozart, Klaviersonate F-Dur KV 332, III. Satz, T. 45–47
Analoge Verfahren lassen sich in den Sequenzen Nr. 2, 5, 8, 11 und 12 beobachten.
Bei der zweiten Verfahrensweise gibt es ebenfalls zwei Motive innerhalb eines Moduls mit zwei Akkorden, die jedoch auf beide Hände verteilt sind und somit eine Art ›Phasenverschiebung‹ bewirken: Das erste Motiv endet auf dem starken Taktteil, während das zweite auf dem schwachen Taktteil beginnt. Das zweite Motiv wiederum endet auf dem starken Taktteil, während das erste auf dem schwachen Taktteil neu beginnt. Für dieses Verfahren gibt die Sequenz Nr. 3 ein Beispiel:
Beispiel 14: ›Gerade‹ und ›ungerade‹ Motive in Sequenz Nr. 3; W.A. Mozart, Klaviersonate a-Moll KV 310, I. Satz, T. 5–7
Dasselbe Verfahren findet sich in den Sequenzen Nr. 4 (zwischen den obersten zwei Stimmen), Nr. 6, 13 und 14, jeweils in unterschiedlicher Ausprägung.
Die Sequenzen Nr. 7 und Nr. 15 (und letztlich auch Sequenz Nr. 1) enthalten nur Akkordtöne in einer ununterbrochenen Reihe von Sechzehntelnoten, Achtelnoten beziehungsweise Achteltriolen. Daher kann man hier keine Motive im eigentlichen Sinne abgrenzen. Dasselbe gilt für die Sequenz Nr. 16 mit ihren Vorhaltslinien in der rechten Hand und der ununterbrochenen Reihe von Sechzehnteltriolen in der linken. In der Sequenz Nr. 10 schließlich fallen die Motive ausnahmsweise mit den Akkord und Modulgrenzen zusammen.
Dichte. Sequenz Nr. 15 ist die kompakteste in unserer Sammlung: Nur zwei Noten pro Akkord reichen aus, um die gesamte Fortschreitung zu durchlaufen. Sequenz Nr. 7 ist die mit drei Noten pro Akkord etwas weniger kompakt. Zumeist benötigt eine Sequenz acht bis zwölf Noten pro Akkord. Die größte Notenzahl findet sich in der Sequenz Nr. 2, mit 14 und 17 Noten (meist Zweiunddreißigstel) für die zwei Akkordtypen.
Vollständigkeit. Grundsätzlich besteht eine Zirkelsequenz aus acht Akkorden. In der musikalischen Praxis umfasst sie jedoch nicht immer die gesamte Reihe von Tonika zu Tonika. Die zwei Sequenzen in der Sonate KV 545 (Nr. 12, 13) zeigen modellhaft die vollständige Reihe von acht Akkorden, in vier Takten und mit vier Durchführungen des Sequenzmoduls. Eben dort jedoch ist der Schlussakkord in seiner Ausarbeitung von den vorangehenden Akkorden unterschieden. Die Sequenzen Nr. 6 und 9 zeigen ebenfalls kleine Änderungen im Schlussakkord. In anderen Sequenzen (Nr. 2, 3, 8) sind die letzten Akkorde mit Texturen belegt, die nicht mehr als Varianten des Sequenzmoduls aufgefasst werden können und sich mitunter über mehrere Takte verbreitern. Gelegentlich sind auch die Anfangsakkorde einer Sequenz anders texturiert als der eigentliche Korpus (Nr. 2, 9, 14). Einige Sequenzen schließlich sind ›übervollständig‹, das heißt, sie umfassen noch einige zusätzliche Akkorde über die reguläre Reihe von Tonika zu Tonika hinaus. Sequenz Nr. 1 und 16, die erste und letzte unseres Katalogs, enthalten Akkorde, die der zentralen Folge vorangehen, Sequenz Nr. 7 geht zweimal durch den ganzen Zirkel.
Mehrstimmigkeit. Viele Sequenzen lassen ihren Ursprung in der Mehrstimmigkeit erkennen. Regelmäßig stößt man auf individuelle Linien, die mit den Stimmverläufen in unseren Beispielen 2 und 3 (mit Dreiklängen) oder 6 und 7 (mit Septakkorden) übereinstimmen. So kann die Oberstimme der Sequenz Nr. 6 als Entsprechung der zweiten Altstimme aus Beispiel 7 gedeutet werden. Die zwei Stimmen in der rechten Hand von Sequenz Nr. 16 folgen dem Sopran und Tenor aus Beispiel 6. Die Intervalle der rechten Hand in der Sequenz Nr. 8 können in längeren Notenwerten ausgeschrieben werden und entsprechen dann Sopran und Alt des Beispiels 6 (in vertauschten Lagen):
Beispiel 15: Reduktion der Mehrstimmigkeit in Sequenz Nr. 8; W.A. Mozart, Klaviersonate F-Dur KV 332, I. Satz, T. 60–64
Die Stimmen der rechten Hand in Sequenz Nr. 5 entsprechen dem Tenor und zweiten Alt in Beispiel 7. Werden die gebrochenen Intervalle der rechten Hand in Sequenz Nr. 7 in mehreren Linien ausgeschrieben, stellt die oberste Linie den zweiten Alt und die unterste den ersten Alt aus Beispiel 7 dar.
Die Bassstimme des Sequenzmodells erscheint zuweilen als ein Alternieren von fallenden Quinten und steigenden Quarten (Nr. 2, 6, 8, 9, 14). In Nr. 8 ist dieses Alternieren durch die satztechnische Ausarbeitung besonders hervorgehoben. In anderen Fällen wechselt die Bassstimme zwischen Grundtönen und Terzen (Nr. 3, 5, 10, 11, 12, 13, 15, 16). So lässt sich die Sequenz Nr. 11 auf folgendes Gerüst reduzieren:
Beispiel 16: Gerüstsatz von Sequenz Nr. 11; W.A. Mozart, Klaviersonate B-Dur KV 333, III. Satz, T. 189–193
Die letzte Viertelnote in der Bassstimme eines jeden Taktes ist gleichzeitig eine Durchgangsnote zur Ausfüllung der fallenden Terz, wie die Septime in jeder zweiten Takthälfte zur Terz des nachfolgenden Akkords.
Die drei Stimmen der rechten Hand in Sequenz Nr. 4 können für die ersten Akkorde (von oben nach unten) als erster Alt, zweiter Alt und Sopran aus Beispiel 7 beschrieben werden, für die weiteren Akkorde als Tenor, Sopran und erster Alt. Sie bilden eine dreistimmige Struktur über dem Dominantorgelpunkt im Bass, so dass folgende Reduktion möglich ist:
Beispiel 17: Reduktion der Mehrstimmigkeit in Sequenz Nr. 4; W.A. Mozart, Klaviersonate a-Moll KV 310, I. Satz, T. 59–61
Akkorde. Im Abschnitt »Zur Theorie der Zirkelsequenz« wurde bereits auf die verschiedenen Harmonisierungsmöglichkeiten hingewiesen: Dreiklänge oder Septakkorde, leitereigene oder leiterfremde Akkorde, letztere üblicherweise in der Funktion von Zwischendominanten. Die von Mozart verwendeten Akkorde sind in Tafel 1 am Ende dieses Beitrags aufgelistet. Die schlichteste Lösung zeigen die beiden Sequenzen des ersten Satzes der C-Dur- Sonate KV 545 (Nr. 12–13): Sie sind durchgängig mit einer einfachen Reihe leitereigener Dreiklänge realisiert, wobei Grundstellung und erste Umkehrung einander ablösen.
Durch Reduktion der Akkorde auf Terzen kann eine Sequenz abermals einfacher realisiert werden. Dieses Verfahren begegnet in den Sequenzen Nr. 5 (geradzahlige Akkorde), 6 (geradzahlige Akkorde), 9 (alle Akkorde), 14 (geradzahlige Akkorde) und 15 (alle Akkorde). In der Sequenz Nr. 2 erscheinen die Akkorde zunächst ebenfalls auf Terzen reduziert, werden jedoch mit der zweiten Viertelnote jedes Taktes zu Dreiklängen vervollständigt.
Die Verwendung von Septimen für jeden Akkord der Sequenz (den ersten und letzten Akkord ausgenommen) ist relativ selten und beschränkt sich auf die Sequenzen Nr. 4 und 8. Das gewöhnliche Verfahren besteht im regelmäßigen Wechsel von Dreiklängen und Septakkorden (Nr. 1, 3, 5, 7, 10 und 14).
Viele Sequenzen enthalten Alterationen, die der Herstellung von Zwischendominanten dienen, beispielsweise durch Duraufhellung, Hinzufügung der kleinen Septime oder Anwendung verminderter Akkorde. Zwischendominanten scheinen vor allem für Sequenzen in Dur-Tonarten charakteristisch zu sein. Das Extrem ist wohl Sequenz Nr. 1: Jeder Akkord kann als eine Zwischendominante gelesen werden, abgesehen vom zweiten Akkord und dem Kadenzschluss. Selbst die eröffnende Tonika (T. 19,1) ist als verminderter Zwischendominantakkord zur darauf folgenden vierten Stufe funktionalisiert.
Die Satzweise der Akkorde in Sequenz Nr. 1 resultiert aus ihrer metrischen Platzierung. Die Akkorde auf der ersten Zählzeit sind jeweils verminderte Septakkorde, diejenigen auf der zweiten Dur-Dreiklänge. Die Akkorde auf der jeweils dritten Zählzeit nehmen mehrfach Alterationen des nach dem Taktstrich folgenden Septakkords vorweg.
Andere Sequenzen sind weniger stark durch Zwischenfunktionen angereichert. Die Sequenzen Nr. 10, 12 und 15 beginnen mit Akkord 5 unseres Modells, der als Zwischendominante zu Akkord 6 fungiert, und enthalten am Ende Akkord 4, realisiert als Zwischendominante zu Akkord 5. Sequenz Nr. 7 zeigt gleichfalls viele Zwischendominanten: Nach den Anfangsakkorden ist jeder weitere Akkord entweder eine einfache Dominante (Akkord 7) oder eine Zwischendominante.
Es ist bemerkenswert, dass in den Moll-Sequenzen nur selten alterierte Akkorde vorkommen. Als Beispiel mag allenfalls die Sequenz Nr. 4 aus der Durchführung des ersten Satzes von KV 310 gelten, wo Alterationen teils als Leittöne, teils als Durchgänge eingefügt sind.
Wiederholung des Sequenzmoduls. Damit von einer Sequenz überhaupt gesprochen werden kann, sollte das Sequenzmodul im betreffenden Passus wenigstens zweimal durchgeführt werden. Obwohl ein Sequenzmodul bei einer Zirkelsequenz schwerer definiert werden kann als bei transponierenden Sequenzen, sind die Wiederholungen doch deutlich wahrnehmbar. In den Zirkelsequenzen der Klaviersonaten Mozarts ist das Sequenzmodul zuweilen nur zweimal unverändert zu finden (Nr. 2, 3, 8, 9), häufiger dreimal (Nr. 4, 5, 6, 10, 14) und in einigen Fällen auch viermal (Nr. 11, 12, 13, 15). Vier Sequenzmodule implizieren acht Akkorde, so dass in diesen Fällen die gesamte Sequenz durchgeführt ist. Liegen drei Sequenzmodule vor, bedeutet dies, dass ein oder zwei Akkorde am Anfang oder am Ende abweichend figuriert oder motivisch eingebunden sind. Sequenzen mit nur zwei Modulen zeigen ein hinzugefügtes Halbmodul oder ein verwandtes Modul, das den eigentlichen Modulen vorausgeht oder ihnen folgt.
Das Modul der Sequenz Nr. 1 ist in mehrfacher Hinsicht bemerkenswert. Hier werden zwei Akkorde innerhalb eines 3/4-Takts berührt, wobei die Oktaven auf dem ersten und zweiten Schlag der linken Hand den Akkordwechsel anzeigen. Die rechte Hand jedoch setzt dem ein Alternieren von steigenden und fallenden Achteltriolen entgegen, so dass sich faktisch eine Zwei-Viertel-Figur ergibt, die dreimal innerhalb von zwei Takten auftaucht: Das Modul der rechten Hand wiederholt sich erst nach vier Akkorden. Insofern ist diese Sequenz die komplizierteste der hier behandelten.
Verschobene Zirkelsequenzen. Bisher wurden Sequenzen als Akkordfortschreitungen beschrieben, die mit der Tonika beginnen und enden (auch wenn in einigen Fällen der Tonikaakkord nicht selbst Teil eines Sequenzmoduls ist). Es gibt jedoch auch eine Anzahl von Sequenzen, bei denen die Tonika in der Mitte der Akkordprogression steht. Mit vier Beispielen (Nr. 4, 10, 11, 15) in drei Sonaten (KV 310, KV 333, KV 570) ist diese Gestalt nicht eben selten. Alle diese Sequenzen beginnen mit Akkord 5 unseres Sequenzmodells, also der VI. Stufe, erreichen über II und V die Tonika und setzen sich dann mit der ›ersten Hälfte‹ des Modells fort. Die Sequenzen Nr. 10, 11 und 15 bringen nach der Tonika die Stufen IV (2), VII (3), III (4) und VI (5); die Sequenz Nr. 4 (dreimal durchgeführt, in e-Moll, a-Moll und d-Moll) endet mit der VII. Stufe. Diese Art von Sequenz – gespielt von Millionen Klavierspielern, doch meines Wissens in der musiktheoretischen Literatur bislang nicht beschrieben – verdient eine Bezeichnung für sich. In Erwartung eines besseren Vorschlags wird sie hier vorläufig ›verschobene Zirkelsequenz‹ getauft.
Zur Lokalisierung der Zirkelsequenzen in den Sonatensätzen Mozarts
Die Mehrzahl der Zirkelsequenzen findet sich in Sätzen, die der Sonatenhauptsatzform folgen.[29] In Anlehnung an William Caplins Classical Form werden wir einzelne Abschnitte des musikalischen Verlaufs (Phrasen) anhand ihrer Funktion innerhalb der jeweiligen Formteile wie Hauptsatz, Seitensatz, Schlussgruppe bzw. Exposition, Durchführung und Reprise beschreiben.[30]
Oft zeigen Formabschnitte selbst eine satzähnliche Binnenstruktur (»sentence«), sofern sie aus einer ersten Phrase mit der Funktion ›thematische Präsentation‹ (»thematic presentation«), weiteren Phrasen als ›Fortsetzung‹ (»continuation«) und einer ›Kadenz‹ (»cadence«) bestehen.[31] Phrasen mit Präsentationsfunktion sind melodisch geprägt und bestehen entweder aus einer (oft zweitaktigen) Grundidee, der eine Wiederholung oder Variation folgt, oder sie zeigen eine Vordersatz-Nachsatz-Beziehung (oft mit zweimal acht Takten). Fortsetzungsphrasen bestehen üblicherweise aus kleineren Fragmenten und können zu Kadenzphrasen führen.
Durchführungen können nach Caplin in einen Eingangsbereich (»pre-core«) und einen Kernbereich (»core«) gegliedert werden. Der Eingangsbereich kann eine satzähnliche Struktur mit eigenen Darstellungs, Fortsetzungs und Kadenzphrasen zeigen. Der Kernbereich besteht nach Caplins Worten aus »einem verhältnismäßig großen Modell (4 bis 8 Takte), einer oder mehreren sequenziellen Wiederholungen, Fragmentation, einer abschließenden Halbkadenz (oder ›Ankunft bei der Dominante‹) und einem postkadenziellen ›Stehen auf der Dominante‹.«[32]
Von hier aus können wir nun der Frage nachgehen, wo und wie die Zirkelsequenzen in den verschiedenen Formteilen der Sonatensätze Mozarts platziert worden sind. Vorausgeschickt sei, dass Zirkelsequenzen wenigstens einmal in jedem Formteil zu finden sind. Am häufigsten kommen sie in Seitensätzen (viermal) und Durchführungen (dreimal) vor, seltener in Überleitungen (zweimal) und Hauptsätzen (einmal).
Zirkelsequenzen in Exposition und Reprise
Der Hauptsatz im Allegro maestoso der a-Moll-Sonate KV 310 entspricht beispielhaft dem von Caplin konstruierten Formmodell. Er besteht aus acht Takten, deren erste vier eine wiederholte zweitaktige Idee enthalten (Darstellungsphrase), während die letzten vier eine Fortsetzungsphrase bilden, die durch eine vollkommene Kadenz abgeschlossen wird. Die Sequenz Nr. 3 hat hier Fortsetzungsfunktion:
KV 310, I. Satz | ||
Takte | 1–4 | 5–8 |
Funktion | Darstellung | Fortsetzung |
Phrasen | Idee + Wiederholung 2+2 | Sequenz Nr. 3 |
Zwei Sonaten zeigen eine Sequenz in der Überleitung zum Seitensatz. Die Überleitung im ersten Satz der F-Dur-Sonate KV 280 kann wiederum als Formteil mit satzähnlicher Binnenstruktur beschrieben werden:
KV 280, I. Satz | |||
Takte | 13–17 | 18–22 | 23–26 |
Funktion | Darstellung | Fortsetzung | Kadenz |
Phrasen | neue Idee | Sequenz Nr. 1 | Halbschluss |
Die Überleitung enthält keine Modulation; sie verweilt in der Haupttonart F-Dur und kadenziert halbschlüssig in einen C-Dur-Dreiklang. Die Sequenz fungiert also auch hier als Fortsetzungsphrase.
Der dritte Satz der F-Dur-Sonate KV 332 hat eine ziemlich kurze Überleitung. Setzt man den Hauptsatz bis T. 35 und den Seitensatz ab T. 50 an, stellt sie sich wie folgt dar:
KV 332, III. Satz | |||
Takte | 36–45 | 46–48 | 49 |
Funktion | Darstellung | Fortsetzung | Kadenz |
Phrasen | Idee + Wiederholung (3+2)+(3+2) d-Moll, C-Dur | Sequenz Nr. 9 C-Dur | Halbschluss C Dur |
Auch mehrere Seitensätze in Mozarts Klaviersonaten enthalten eine Sequenz. Der Seitensatz des ersten Satzes der B-Dur-Sonate KV 281 steht in F-Dur und kann folgendermaßen analysiert werden:
KV 281, I. Satz | |||||
Takte | 18–21 | 22–26 | 27–34 | 34–37 | 38–40 |
Funktion | Seitenthema 1 Darstellung | Fortsetzung | Seitenthema 2 Darstellung | Fortsetzung/ Kadenz | Schluss |
Phrasen | Idee + Wiederholung 2+2 | Sequenz Nr. 2 | Idee + Wiederholung 4+4 | Idee + Wiederholung 2+2 | ›Codetta‹[33] zweimal, dann Schlussakorde |
Die Sequenz, die wiederum in einer Fortsetzungsphrase platziert ist, verbindet die beiden Seitenthemen derart, dass die Schluss-Tonika des ersten Seitenthemas als Akkord 1 der Sequenz fungiert, während das zweite Seitenthema die Akkorde 7 und 8 beinhaltet.
Der Seitensatz des ersten Satzes der F-Dur-Sonate KV 332 folgt einem ähnlichen Schema:
KV 332, I. Satz | |||||||
Takte | 41–56 | 56–59 | 60–65 | 66–69 | 70–82 | 82–85 | 86–93 |
Funktion | Seitenthema 1 Darstellung |
| Fortsetzung | Kadenz | Seitenthema 2 Darstellung | Fortsetzung / Kadenz | Schluss |
Phrasen | Vorder + Nachsatz 8+8 | Ein-leitung | Sequenz Nr. 8 c-Moll | Halbschluss | Idee + Wiederholung 6+6 | Idee + Wiederholung 2+2 | zweimal ›Codetta‹ + Schlussakkorde |
Die Sequenz wird durch vier Takte (zwei Dominant-Tonika-Paare) eingeleitet, die der Modulation in die Variante (c-Moll) dienen und zugleich das Texturmotiv der Sequenz vorführen. Die Sequenz endet mit Akkord 7 in T. 65 auf der Dominante, die noch um vier Takte verlängert wird. Die abschließende Tonika (Akkord 8) wird erst mit der neuen Idee des zweiten Seitenthemas in T. 76 erreicht.
Der erste Satz der B-Dur-Sonate KV 333 enthält eine Sequenz im Seitensatzbereich der Reprise:
KV 333, I. Satz | ||||||
Takte | 119–134 | 135–142 | 143–146 | 147–152 | 152–160 | 161–165 |
Funktion | Seitenthema 1 Darstellung | Fortsetzung |
| Kadenz | Seitenthema 2 Darstellung | Schluss |
Phrasen | Vorder + Nachsatz 8+8 | Idee + Wiederholung + Kadenz 2+2+4 | Sequenz Nr. 10 | Kadenz | Idee + Wiederholung 4+5 | zweimal Codetta + Schlussakkorde |
Wiederum gibt es zwei Seitenthemen. Dem ersten folgt eine ziemlich lange Fortsetzungsphrase, dem zweiten unmittelbar eine Schlussphrase. Die Sequenz ist ungefähr in der Mitte der Fortsetzungsphrase nach dem ersten Seitenthema platziert. Diesmal handelt es sich um eine ›verschobene Sequenz‹, eine Sequenz also, die weder mit der Tonika beginnt noch endet. Die vorangehende und die nachfolgende Phrase (T. 135–142 bzw. 147–152) zeigen jeweils die Tonika als Abschluss einer vollkommenen authentischen Kadenz. Die Sequenz beginnt mit Akkord 5 (Vi. Stufe). Der erste Akkord eines jeden Taktes ist dominantisch. Die jeweils zweiten Akkorde bauen sich auf den Basstönen c, b, a und g auf, die eine fallende Linie bilden. Sie führen zur F-Dur-Harmonie, welche die nächsten Takte beherrscht, bevor eine doppelte vollkommene Kadenz den Passus abschließt. In dieser Interpretation ist die Sequenz eine Einleitung zur kadenziellen Phrase in den Takten 147–152.
Der Seitensatz des ersten Satzes der C-Dur-Sonate KV 545 hat nur ein Thema:
KV 545, I. Satz | |||||
Takte | 13 | 14–17 | 18–21 | 22–25 | 26–28 |
Funktion |
| Seitenthema Darstellung | Fortsetzung | Kadenz | Schluss |
Phrasen | Einleitung | Idee + Wiederholung 2+2 | Sequenz Nr. 12 | Kadenz | zweimal Codetta + Schlussakkorde |
Die Sequenz fungiert als Fortsetzungsphrase des Seitenthemas. Die oben betrachteten Beispiele lassen die Folgerung zu, dass Zirkelsequenzen fast immer in Fortsetzungsphrasen platziert sind, die auf fester gefügte thematische Komplexe folgen. Ein solcher thematischer Komplex kann sowohl der Hauptsatz oder Seitensatz als auch eine neue Idee innerhalb einer Überleitung sein.
In welchem Umfang werden nun die Sequenzen, die in der Exposition eines sonatenförmigen Satzes begegnen, in der Reprise wiederholt bzw. harmonisch transformiert? Gewöhnlich geschieht dies relativ schematisch und in der erwarteten Tonart, doch gibt es Ausnahmen. Die Sequenz in der Überleitung der F-Dur-Sonate KV 280 (Nr. 1) beispielsweise wird in der Reprise auf ungewöhnliche Weise wiederholt. Die Überleitung hat keine modulierende Funktion, so dass es eigentlich möglich gewesen wäre, sie ohne Änderung zu übernehmen. Vielleicht hat Mozart die Sequenz aus eben diesem Grund variiert. Die Takte 18, 20 und 22 der Exposition werden in den Takten 100, 102 und 104 der Reprise nahezu unverändert rekapituliert, die dazwischen liegenden Takte 20 und 22 hingegen nicht. Die Takte 101 und 103 sind vielmehr gleichsam gespiegelte Fassungen der Takte 20 und 22: Die fallenden kleinen Sekunden der linken Hand sind durch steigende kleine Sekunden der rechten Hand ersetzt. Der Akkordverlauf ist ebenfalls verändert: Die originale Fortschreitung in der Exposition kann als G C F B E A D G C F abstrahiert werden; in der Reprise dagegen lautet sie G C A D E A F B C F.
Beispiel 18: Unterbrochene Sequenz in der Überleitung der Reprise; W.A. Mozart, Klaviersonate F-Dur KV 280, I. Satz, T. 100–104
Die neue Form der Sequenz erlaubt jedoch noch eine alternative Deutung. So können die Takte 100–104 als eine Folge von fünf Akkorden auf dem jeweils zweiten Taktschlag gelesen werden, und zwar mit den Grundtönen c, d, a, b und f. Jeder Akkord wird von einer Zwischendominante in Gestalt eines verminderten Septakkords angezielt. Zusammen mit dem F-Dur-Akkord in T. 99 entsteht so eine Fortschreitung I-V-VI-III-IV-I, die auch als ›Dur-Moll-Parallelismus‹ bekannt ist.[34] Die Akkordpaare I-V, VI-III und IV-I können als drei aufeinander folgende zweitaktige Sequenzmodule beschrieben werden, mit einem Quartfall innerhalb des Moduls und einer fallenden Terz als Transpositionsintervall.[35] Die Sequenzfassung der Reprise unterscheidet sich von jener der Exposition dadurch, dass die Noten des dritten Taktschlags nicht den ersten Akkorden des Folgetaktes angepasst werden, sondern den Akkorden des vorangehenden zweiten Taktschlags.
Diese alternative Deutung nun lässt sich auch auf das Erscheinen der gleichen Sequenz in der Exposition anwenden. Analog zu den Takten 100–105 können die Takte 19–23 als eine Folge von Dreiklängen beschrieben werden, die jeweils durch verminderte Zwischendominantakkorde einkadenziert werden. Die fünf Akkorde bilden hier die einfache Reihe C-Dur (T. 18), B-Dur (T. 19), A-Dur (T. 20), G-Dur (T. 21) und F-Dur (T. 22), die eine diatonisch fallende Quinte von der Dominante bis zur Tonika umschließt.
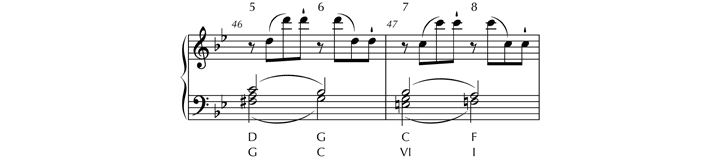
Der erste Satz der B-Dur-Sonate KV 333 zeigt das umgekehrte Verfahren: Die Sequenz im Bereich des Seitenthemas ist nur in der Reprise (Nr. 10), nicht in der Exposition aufzuweisen. In der Exposition findet sich in entsprechender Position lediglich eine rudimentär sequenzähnliche Erscheinung: Die der Sequenz vorangehenden Takte 43–46 ähneln der Parallelstelle in der Reprise zwar, doch findet sich anstelle der Zirkelsequenz lediglich eine zweitaktige transponierende Sequenz mit der Grundtonfortschreitung D G C F und einem wiederholten eintaktigen Sequenzmodul (Nr. 9, T. 46–47). Dasselbe Modul ist in der Reprise zur vollständigen Sequenz ausgebaut.
Beispiel 19: Rudimentäre (transponierende) Sequenz im Seitensatz der Exposition; W.A. Mozart, Klaviersonate B-Dur KV 333. I. Satz, T. 46–47
Normalerweise wird das Material von Sequenzen aus dem Expositionsteil nicht in die Durchführung integriert. Eine Ausnahme bildet der erste Satz der F-Dur-Sonate KV 332: Die auffällige Textur der Sequenz Nr. 8 mit dem ›contre-temps‹ in der rechten Hand spielt hier eine wichtige Rolle in der Durchführung. Diese beginnt mit einer wiederholten achttaktigen Phrase, teilbar in zwei viertaktige Phrasen, die den Eindruck einer Vordersatz-Nachsatz-Beziehung erwecken. Hierauf folgt eine Wiederkehr der Einleitung zur Sequenz wie in der Exposition. Diese neunzehn Takte können im Sinne Caplins als unvollständiger Eingangsbereich betrachtet werden. Ihnen folgt der Kernbereich mit einer Phrase, welche die Figuren der Sequenz Nr. 8 übernimmt, ohne jedoch eine Zirkelsequenz zu bilden. Stattdessen entwickelt sich eine Akkordfolge in Dominant-Tonika-Beziehungen, je zweimal in C-Dur, g-Moll und d-Moll.
Zirkelsequenzen in der Durchführung
Sequenzen begegnen bei Mozart auch in den Durchführungen sonatenförmiger Sätze. Die Durchführung der a-Moll-Sonate KV 310 soll hier als erstes Beispiel dienen. Die folgende Analyse zeigt die Abfolge in Phrasen:
KV 310, I. Satz | |||||||
Takte | 50–53 | 54–57 | 58–61 | 62–65 | 66–69 | 70–73 | 73–79 |
Bereich | Eingangsbereich (pre-core) | Kernbereich (core) | |||||
Phrase | Idee + Wiederholung 2+2 | Fortsetzung | Sequenz Nr. 4 | Sequenz Nr. 4 | Sequenz Nr. 4 | Sequenz Nr. 5 | Halbschluss |
Tonart | C-Dur | modulierend | e-Moll | a-Moll | d-Moll | a-Moll | a-Moll |
Diese Durchführung ist in der Tat von Sequenzen beherrscht: Die Sequenz Nr. 4 erscheint dreimal nacheinander in e-Moll, a-Moll und d-Moll. Sie wird jeweils durch Akkord 5 im Sinne unseres Modells eröffnet und schließt mit Akkord 3 (der hier zugleich als Dominante für den folgenden Sequenzabschnitt fungiert). Es handelt sich also um eine verschobene Sequenz, die schon aufgrund des Dominantorgelpunkts im Bass nicht leicht herauszuhören ist. Trotzdem gibt es zur Deutung der Akkordfolge als Zirkelsequenz keine Alternative: Die Überlappung der Motive in den beiden Oberstimmen und die mehrstimmige Gesamtstruktur belegen ihren sequenzierenden Charakter. Dem dritten Auftreten von Sequenz Nr. 4 (in d-Moll) folgt unmittelbar eine weitere Zirkelsequenz (Nr. 5 in a-Moll), deren Erscheinung im Vergleich zur vorangegangenen relativ schlicht und modellhaft ist.
Die Durchführung des ersten Satzes der C-Dur-Sonate KV 545 ist mit nur dreizehn Takten von rudimentärer Kürze. Sie kann als eine Durchführung beschrieben werden, die entweder nur aus einem Kernbereich mit transponierenden Sequenzen oder gar nur aus einem Eingangsbereich (im Sinne Caplins) besteht. Letztere Auffassung liegt der folgenden Analyse zugrunde:
KV 545, I. Satz | ||||||
Takte | 29–30 | 31–32 | 33–34 | 35–36 | 37–40 | 41 |
Funktion | Darstellung | Fortsetzung | Darstellung | Fortsetzung |
| Kadenz |
Phrase | Idee + Wiederholung | Überleitung | Idee + Wiederholung | Überleitung | Sequenz Nr. 13 | Halbschluss |
Tonart | g-Moll | d-Moll | a-Moll | F-Dur | ||
Die Durchführung des ersten Satzes der B-Dur-Sonate KV 570 enthält eine größere Breite differenzierbarer Phrasen und kann in einen Eingangs- und einen Kernbereich geteilt werden:
KV 570, I. Satz | |||||||
Takte | 80–87 | 88–94 | 95–100 | 101–108 | 109–116 | 117–123 | 124–130 |
Bereich | Eingangsbereich (pre-core) | Kernbereich (core) | |||||
Phrase | Idee + Wiederholung Einl. +4+3 | Fortsetzung | Kadenz Halbschluss | Idee + Wiederholung 4+4 | Idee + Wiederholung 4+4 | Sequenz Nr. 14 | Kadenz Halbschluss |
Tonart | Des-Dur | f-Moll c-Moll g-Moll | g-Moll | c-Moll | c-Moll C-Dur (als Zwischendominante zu f-Moll) | c-Moll | b-Moll B-Dur |
Die Durchführung verarbeitet einen großen Teil des Expositionsmaterials. Die Phrasen des Eingangsbereichs (T. 80–87, 88–94 und 95–100) entsprechen Abschnitten aus der Überleitung in der Exposition (T. 23–29, 30–34 und 35–40). Das Motiv, das den Kernbereich einleitet (T. 101–108), entspricht einer Phrase des Seitensatzes (T. 41–48), bestehend aus einem Dreiklangsmotiv in der linken Hand und einer Gegenbewegung aus diatonisch fallenden Achteln im Bass. In den Takten 101–116 der Durchführung erscheint dieses Motiv zweimal, jeweils mit der Dreiklangsfigur in der rechten Hand und der Achtelfigur in der linken. Zusammen bilden sie das zweitaktige Motiv, das schließlich als Sequenzmodul fungiert.
Zirkelsequenzen in rondoförmigen Sätzen
Drei Sequenzen finden sich in den rondoförmigen Finalsätzen der Sonaten in a-Moll KV 310, D-Dur KV 311 und D-Dur KV 576. Das Rondo des dritten Satzes der a-Moll-Sonate KV 310 enthält dreimal den Refrain, zwei Couplets und eine abschließende Coda. Sequenz Nr. 6 findet sich im ersten Couplet (T. 21–106), das die Funktion des Seitensatzes übernimmt:
KV 310, III. Satz | |||||||||||
Takte | 21–28 | 29–36 | 37–44 | 45–49 | 50–59 | 60–63 | |||||
Funktion | Überleitung | Seitensatz Darstellung | Fortsetzung |
|
|
| |||||
Phrase | Phrase | Idee + Wiederholung 4+4 | Linearsequenz + Kadenz | Linearsequenz + Kadenz | Idee + Wiederholung (2+2)+(2+2+2) | Linearsequenz | |||||
Tonart | C-Dur | c-Moll C-Dur | a-Moll C-Dur | a-Moll C-Dur | C-Dur, d-Moll, C-Dur, d-Moll, e-Moll | a-Moll e-Moll | |||||
KV 310, III. Satz | |||||||||||
Takte | 64–71 | 72–79 | 80–87 | 88–95 | 96–106 | ||||||
Funktion | Seitensatz Darstellung | Fortsetzung |
|
| Kadenz | ||||||
Phrase | Idee + Wiederholung | Linearsequenz | Linearsequenz | Sequenz Nr. 6 | Halbschluss | ||||||
Tonart | e-Moll | e-Moll | e-Moll | a-Moll | a-Moll | ||||||
Der Seitensatz, eine wiederholte viertaktige Idee, erscheint zunächst in c-Moll, dann in C-Dur (T. 29–36) und schließlich in e-Moll (T. 64–71). Ihm folgen jeweils längere Fortsetzungsphrasen, die von fallenden Linearsequenzen dominiert sind. Die Zirkelsequenz Nr. 6 läuft in einen kadenzierenden Passus aus, der das Couplet beendet. Im zweiten Couplet dieses Rondos und in der Coda begegnen viele Teile aus dem ersten Couplet erneut, nicht jedoch die Zirkelsequenz: Während sie in Couplet 1 (= Seitensatz) der Rückführung von e-Moll nach a-Moll dient, ist sie nun, da Haupt- und Seitensatz gleichermaßen in a-Moll stehen, unnötig.
Das Rondo der D-Dur-Sonate KV 311 enthält vier Refrains und drei Couplets. Das erste und dritte Couplet fungieren als Seitensätze (analog zu Exposition und Reprise einer Sonatenform); das zweite Couplet entspricht einer Durchführung, so dass man von einem Sonaten-Rondo sprechen kann. Die Zirkelsequenz findet sich im Durchführungscouplet, das folgendermaßen beschrieben werden kann:
KV 311, III. Satz | |||||||
Takte | 102–110 | 110–118 | 119–132 | 133–136 | 137–154 | 158–172 | 173 |
Bereich | Eingangsbereich (pre-core) | Kernbereich (core) | |||||
Phrase | Idee + Wiederholung | Wiederholung Kadenz | Vorder + Nachsatz | Sequenz Nr. 7 | Vorder + Nachsatz | Idee + Wiederholung | Cadenza Halbschluss |
Tonart | G-Dur | G-Dur e-Moll D-Dur h-Moll | h-Moll | D-Dur | G-Dur | e-Moll d-Moll A-Dur D-Dur | D-Dur |
Die Sequenz findet sich etwa in der Mitte des Couplets, umgeben von zwei Phrasen, die jeweils in Vorder- und Nachsatz gegliedert werden können (T. 119–132 und 137–154). Der ersten dieser Phrasen (mit sequenzierend wiederholten Motiven) geht eine Kadenz voran; der zweiten folgt ein dreimal wiederholtes Motiv (T. 158–172), das auf den Anfang des Couplets (T. 102–110) zurückgreift. Dadurch erhält der Mittelteil des Couplets (T. 102–173) eine symmetrische Struktur, in deren Zentrum die Sequenz steht.
Der dritte Rondo-Satz mit einer Zirkelsequenz ist der Schlusssatz der D-Dur-Sonate KV 576. Dieses Rondo enthält drei Refrains (T. 1–20, 54–84, 163–184) und zwei Couplets, die als Seitensätze beschrieben werden können. Das erste Couplet (T. 20–64) steht erwartungsgemäß in der Dominante A-Dur. Das zweite Couplet (T. 84–182) ist fast zweimal so lang wie das erste und enthält einen durchführungsähnlichen Abschnitt, bevor das Seitenthema in D-Dur wiederkehrt (T. 117). Von hier an folgt das zweite Couplet im Großen und Ganzen dem Verlauf des ersten. Sequenz Nr. 16 kommt in beiden Couplets vor, im ersten in A-Dur, im zweiten in D-Dur. Das erste Couplet ist folgendermaßen gebaut:
KV 576, III. Satz | |||||||||||
Takte | 16–20 | 20–23 | 23–25 | 26–29 | 30–33 | 34–39 | 40–46 | ||||
Funktion | Überleitung Darstellung | Fortsetzung | Kadenz | Seitenthema 1 Darstellung | Fortsetzung | Fortsetzung | Kadenz | ||||
Phrase | Idee + Wiederholung |
| Halbschluss | Idee + Wiederholung 2+2 | gleiche Idee | gleiche Idee Halbschluss | Ganzschluss | ||||
Tonart | D-Dur | D-Dur | D-Dur | A-Dur | A-Dur | A-Dur | A-Dur | ||||
Takte | 46–48 | 49–50 | 50–58 | 58–64 | |||||||
Funktion |
|
| Seitenthema 2 Darstellung | Überl. | |||||||
Phrase | Sequenz Nr. 16 | Kadenz | Vorder + Nachsatz | Halbschluss | |||||||
Tonart | A-Dur | A-Dur | A-Dur | D-Dur | |||||||
Die Sequenz steht am Ende einer längeren Reihe von Fortsetzungsphrasen hinter dem ersten Seitenthema. Die Sechzehnteltriolen im Bass der Sequenz setzen den Bewegungsablauf fort, der in T. 40 beginnt. Die Sequenz Nr. 16 erscheint ein weiteres Mal im zweiten Couplet, das der Seitensatz-Reprise entspricht, nunmehr als recht getreue Transposition in die Tonika D-Dur.[36]
Schlussbemerkungen
Was hat die Untersuchung der Zirkelsequenzen in Mozarts Klaviersonaten erbracht? Zunächst einmal wurde deutlich, wie vielfältig Zirkelsequenzen in der musikalischen Praxis erscheinen können. Für Mozart gab es kein Standardverfahren für die Ausarbeitung einer Zirkelsequenz. Stattdessen zeigen sich große Varianzen in der Behandlung fast jedes Aspekts (wie der Wahl der Textur, der Akkorde, der Stimmführung, der Motive, der Verbindung mit vorausgegangenen und nachfolgenden Phrasen). Die Untersuchung hat außerdem gezeigt, wie sehr sich Zirkelsequenzen von transponierenden Sequenzen unterscheiden. Charakteristisch für die Zirkelsequenz sind Akkordprogressionen in fallenden Quinten, der zyklische Verlauf (beginnend und endend mit der Tonika), die Figuration mit akkordübergreifenden Motiven und die häufig lineare Satzweise, die auf den Ursprung des Modells in der mehrstimmigen Musik des siebzehnten Jahrhunderts verweist. Die Technik der Zirkelsequenz kann auch für Fortschreitungen benutzt werden, welche die Tonika in der Mitte zeigen, wofür hier der Terminus ›verschobene Zirkelsequenz‹ vorgeschlagen wurde. Die Analyse von Zirkelsequenzen mit Hilfe von Kategorien, die für transponierende Sequenzen entwickelt wurden, wird dem Phänomen letztlich nicht gerecht.
Die Untersuchung der formalen Disposition von Zirkelsequenzen in den Sonaten Mozarts erwies vor allem ihre bevorzugte Eignung für Fortsetzungsphrasen nach der Einführung thematischen Materials. Dass sie häufiger in Seitensatz- als in Hauptsatzbereichen vorkommen, ist kein Zufall: Als zyklische Gestalten haben Zirkelsequenzen eine die Tonart bestätigende Eigenschaft, die im Bereich der Sekundärtonart hilfreicher als im Bereich der Haupttonart zu sein scheint. Wenn ein sonatenförmiger Satz zwei Seitenthemen aufweist, findet sich die Zirkelsequenz stets nach dem ersten, niemals nach dem zweiten. Das erste Couplet eines Rondos, das so oft dem Seitensatz der Sonatenhauptsatzform entspricht, enthält daher gleichfalls oft eine Zirkelsequenz. Anders als in den Seitensatzbereichen von Sonatensätzen platziert Mozart sie freilich meist am Ende des Couplets. Niemals indes begegnen Zirkelsequenzen, zumindest in Mozarts Klaviersonaten, in den Schlussabschnitten einer Exposition oder Reprise, ebenso wenig in einer Coda. Der Kernbereich einer Durchführung enthält gewissermaßen per definitionem sequenzartige Verläufe, die jedoch nicht notwendigerweise Zirkelsequenzen bilden müssen.
Natürlich finden sich Zirkelsequenzen auch in anderen Werken Mozarts. Es muss vorläufig offen bleiben, ob eine Untersuchung der Sequenzen in anderen Werkgattungen prinzipiell andere Ergebnisse erbrächte als die vorliegende Studie.
| Akkord | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Stufe | I | IV | VII | III | VI | II | V | I |
| Leitereigene Dreiklänge | Dur | Dur | Verm. | Moll | Moll | Moll | Dur | Dur |
| Leitereigene Septakkorde | Dur7 | Dur7 | Verm.7 | Moll7 | Moll7 | Moll7 | Dom7 |
|
Sequenz |
|
|
|
|
|
|
|
|
|
Nr. 1 | F-Dur | Verm.7 | Dur | Verm.7 | Dur | Verm.7 | Verm.7 Dur | Dom7 Verm.7 | Verm.7 Dur |
Nr. 2 | F-Dur (B-Dur) |
| Dur | Verm. | Moll | Moll | Moll |
|
|
Nr. 7 | D-Dur | Dur7 Dur | Dur Dom7 | Verm.7 Verm. | Moll Dom7 | Dom7 Moll | Moll Dom7 | Dom7 Moll | Dur Dom7 |
Nr. 9 | C-Dur | Dur | Dur | Verm. | Moll | Moll | Moll | Dur | Dur |
Nr. 10 (verschoben) | B-Dur | Dur | Dur7 | Verm. | Dom7 | Dom7 Moll | Moll | Dom7 | Dur |
Nr. 11 (verschoben) | B-Dur | Dur(7) | Dur7 | Verm.(7) | Dom7 | Dom7 Moll(7) | Moll(7) Moll7 | Dom7 | Dur(7) |
Nr. 12 | G-Dur | Dur | Dur | Verm. | Moll | Moll | Moll | Dur | Dur |
Nr. 15 (verschoben) | B Dur | Dur | Dur | Verm. | Dur | Dur Moll | Moll | Dur | Dur |
Nr. 16 | A-Dur (D-Dur) | Dur7 | Dur7 | Verm. | Dom7 | Dom7 Moll | Moll Dom7 | Dom7 Dom7 | Dur Dur |
Tafel 1a: Die Akkorde in den Zirkelsequenzen der Klaviersonaten Mozarts: Dursequenzen
| Akkord | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Stufe | I | IV | VII | III | VI | II | V | I |
| Leitereigene Dreiklänge | Moll | Moll (Dur) | Dur (Verm.) | Dur (Überm.) | Dur | Verm. | Dur | Moll |
| Leitereigene Septakkorde | Moll7 | Moll7 (Dom7) | Dom7 (Verm.7) | Dur7 (Überm.7) | Dur7 | Verm.7 | Dom7 |
|
Sequenz |
|
|
|
|
|
|
|
|
|
Nr. 3 | a-Moll | Moll | Moll7 | Dur | Dur7 | Dur |
|
|
|
Nr. 4 (verschoben) | e-Moll (a-Moll) (d-Moll) | Moll | Dom7 | Verm.7 |
| Dur7 | Hverm.7 | Dom7 | Moll |
Nr. 5 | a-Moll |
| Moll | Dom7 | Dur | Dur7 | Verm. | Dom7 | Moll |
Nr. 6 | a-Moll | Moll | Moll(7) | Dom7 | Dur(7) | Dur7 | Verm.(7) | Dom7 |
|
Nr. 8 | c-Moll (f-Moll) | Moll | Moll7 | Dom7 | Dur7 | Dur7 | Verm.7 | Dom7 |
|
Nr. 13 | a-Moll | Moll | Moll | Dur | Dur | Dur | Verm. | Dur | Moll |
Nr. 14 | c-Moll |
| Moll | Dom7 | Dur | Dur7 | Verm. | Dom7 | Moll |
Tafel 1b: Die Akkorde in den Zirkelsequenzen der Klaviersonaten Mozarts: Mollsequenzen
Bei den leitereigenen Dreiklängen und Septakkorden der Mollsequenzen sind die Akkorde, die durch Alteration von Sexte oder Septime der Grundtonart entstehen würden, in Klammern angegeben. Steht eine (7) in Klammern hinter dem Akkord, bedeutet dies, dass ihm die Septime erst später hinzugefügt wird.
Dur = Durdreiklang; Dur7 = Großer Septakkord;
Moll = Molldreiklang; Moll7 = Kleiner Septakkord;
Verm. = Verminderter Dreiklang; Verm.7 = Verminderter Septakkord;
Überm. = Übermäßiger Dreiklang; Überm.7 = Übermäßiger Septakkord;
Dom7 = Dominantseptakkord.
KV | Satz | Tonart | Sequenz | Exposition | Durchführung | Reprise | ||||
Hauptsatz | Überleitung | Seitensatz | Durchführung | Hauptsatz | Überleitung | Seitensatz | ||||
280 | I. | F-Dur | Nr. 1 |
| 18–23: F-Dur |
|
|
|
|
|
281 | I. | B-Dur | Nr. 2 |
|
| 21–30: F-Dur |
|
|
| 91–99: B-Dur |
310 | I. | a-Moll | Nr. 3 | 5–9: a-Moll |
|
|
| 84–88: a-Moll |
|
|
Nr. 4 |
|
|
| 59–61: e-Moll 63–65: a-Moll 67–69: d-Moll |
|
|
| |||
Nr. 5 |
|
|
| 70–72: a-Moll |
|
|
| |||
332 | I. | F-Dur | Nr. 8 |
|
| 60–65: c-Moll |
|
|
| 194–201: f-Moll |
III. | F-Dur | Nr. 9 |
| 46–48: C-Dur |
|
|
| 179–183: F-Dur |
| |
333 | I. | B-Dur | Nr. 10 |
|
|
|
|
|
| 142–146: B-Dur |
545 | I. | C-Dur | Nr. 12 |
|
| 81–21: G-Dur |
|
|
| 63–66: C-Dur |
Nr. 13 |
|
|
| 37–40: a-Moll |
|
|
| |||
570 | I. | B-Dur | Nr. 14 |
|
|
| 117–123: c-Moll |
|
|
|
Tafel 2: Zirkelsequenzen in Sätzen aus Mozarts Klaviersonaten in Sonatenhauptsatzform
Anmerkungen
Dieser Beitrag ist in kürzerer Form auf Englisch erschienen in Dutch Journal of Music Theory 11/3 (November 2005), 178–202. Ich danke Michiel Schuijer (Den Haag) und Thomas Christensen (Chicago) für ihre hilfreichen Bemerkungen bezüglich einer früheren Fassung, ebenso den Herausgebern dieser Ausgabe der ZGMTH für die sprachliche Bearbeitung des deutschen Textes. | |
Drabkin 2001. | |
Siehe Caplins Beispiele 2.11.f (mit Durdreiklängen) und 2.11.g (mit Septakkorden). | |
Dieses Beispiel entspricht Caplin 1998, Beispiel 2.11.a. | |
Der Terminus »Sequence« fehlt jedoch im Register von Christensen 2002. | |
Thomas Christensen gab mir Hinweise zu zwei amerikanischen Dissertationen zum Thema »Sequenz« (Moreno 1993 und Ricci 2004). Leider konnte ich diese Dissertationen nicht einsehen; vgl. auch Moreno 2000, Ricci 2002. Moreno bespricht hauptsächlich transponierende Sequenzen aus dem Musikschrifttum des frühen neunzehnten Jahrhunderts; Ricci enthält eine formale Beschreibung der transponierenden Sequenz mit Methoden der pitch-class set theory. Ich danke Adam Ricci für die Zusendung einer Kopie seiner Artikel (die in einer außerhalb der USA schwer zugänglichen Zeitschrift erschienen sind). Nach Abschluss dieses Beitrags wurde ich durch Harmuth Kinzler (Osnabrück) freundlicherweise auf einige relevante deutsche Beiträge über Quintfallsequenzen bzw. Zirkelsequenzen aufmerksam gemacht, insbesondere Troschke 1995, Holtmeier 2000 und Kinzler 2003. | |
Drabkin 2001. | |
Drabkin 1980. | |
Crocker/Caldwell/Planchart 2001. | |
Pfannkuch 1998. | |
Kruckenberg 1998. | |
Louis/Thuille 1912, 108: »Nebenharmonien in Dur«, 130: »in Moll«, 141: »im äolischen Moll«. | |
Anton Bruckner, Fünfte Symphonie, Adagio, Takte 174–175, und J.S. Bach, Toccata d-Moll, BWV 538, T. 31–32. | |
Mulder 1952, 29–30. Das einzige Musikbeispiel mit einer Zirkelsequenz ist ein Fragment aus dem Offertorium von Mozarts Requiem (»Ne absorbeat«), aber dieses Beispiel dient lediglich zur Erläuterung der Dur-Moll-Sexte (55). | |
Forte 1962, 101–102. | |
Ebd., 94, 149–151 bzw. 140, 225. | |
Piston 1976, 212–224. | |
Dahlhaus 1967, 133. | |
Ebd., 133. | |
Aldwell/Schachter 1989, 246–269. | |
G.F. Händel, Royal Fireworks Music, Bourée, und Concerto grosso, op. 6,6, Musette. W.A. Mozart, Sonate KV 545, I. Satz, T. 20–28. | |
Aldwell/Schachter 1978, 410–417. | |
Im französischen Musikschrifttum werden Sequenzen ›marches d’harmonie‹ genannt, vgl. Koechlin 1927, Bd. 1, 46–47. | |
Caplin 1998, 28–31. | |
Taruskin 2005, Bd. 2, 185–192. | |
Ebd., 185. | |
Zum Beispiel in Sonata IV, Allegro, T. 25–26; Presto, T. 26–29; Sonata VI, letztes Allegro, T. 60–63; Sonata IX, Allegro, T. 12–13 und 28–30. | |
Vgl. die analoge ›Beschleunigung‹ am Ende der Sequenz in Beethovens Hammerklavier-Sonate, I. Satz, T. 70–74. | |
Zwei Sequenzen werden im Folgenden nicht behandelt: Sequenz Nr. 11, die in der Cadenza des dritten Satzes der B-Dur-Sonate KV 333 zu finden ist, und Nr. 15 aus dem dritten Satz der B-Dur-Sonate KV 570, einem Satz mit einzigartiger Form, die nicht nach einem einfachen Schema beschrieben werden kann. | |
Caplin 1998. | |
Ebd., 35–45. | |
Ebd., 254 (Glossary). | |
»Codetta« bezeichnet bei Caplin den Schlussabschnitt eines Binnenformteils; vgl. weiter oben. | |
Dieser würde genau genommen allerdings den d-Moll-, nicht den D-Dur-Dreiklang einschließen, der modulierend wirkt. | |
Vgl. dazu die Analyse von Ludwig Holtmeier (2000). | |
Das zweite Couplet dieses Satzes enthält von T. 87 (letzte Achtelnote) bis 89 (erste Achtelnote) eine modulierende Quintfallsequenz (mit den Grundtönen e-a-d-g-c-f, deren Ziel eine Modulation von a-Moll zu F-Dur ist) und in den Takten 108–111 eine unvollständige Zirkelsequenz in h-Moll mit den Stufen I (H)-IV (E)-VII (A)-IV (D)-G (VI), deren letzter Akkord als Subdominante nach D-Dur zurückführt. |
Literatur
Aldwell, Edward / Carl Schachter (1978), Harmony and Voice Leading, San Diego: Harcourt, Brace, Jovanovich.
Caplin, William E. (1998), Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven, New York: Oxford University Press.
Christensen, Thomas (Hg.) (2002), Cambridge History of Western Music Theory, Cambridge: Cambridge University Press.
Crocker, R.L. / J. Caldwell / A.E. Planchart (2001), Art. »Sequence (I)«, in: New Grove Dictionary of Music and Musicians, 2. Aufl. London: MacMillan, Bd. 23, 91–107.
Dahlhaus, Carl (1967), Untersuchungen über die Entstehung der harmonischen Tonalität, Kassel u.a.: Bärenreiter.
Drabkin, William (1980), Art. »Sequence (II)«, in: New Grove Dictionary of Music and Musicians, London: MacMillan, Bd. 17, 156.
––– (2001), Art. »Sequence (II)«, in: New Grove Dictionary of Music and Musicians, 2. Aufl. London: MacMillan, Bd. 23, 107–108.
Forte, Allen (1962), Tonal Harmony in Concept and Practice, New York: Holt, Rinehart & Winston.
Holtmeier, Ludwig (2000), »Zur Komplexität Mozarts. Analytischer Versuch über eine Sequenz«, Musik & Ästhetik 4/16, 5–23.
Kinzler, Hartmuth (2000), »Vier Quintfallsequenzfälle und ein Beinahe-Quintparallelenfall: Notizen aus der musiktheoretischen Provinz zu Chopin, Bach, Brahms, Beethoven und Mozart«, in: Musik und Leben: Freundesgabe für Sabine Giesbrecht zur Emeritierung, hg. von Hartmuth Kinzler, Osnabrück: Universität Osnabrück, 258–302.
Koechlin, Charles (1927), Traité de l’harmonie, 3 Bde., Paris: Eschig 1947/58.
Louis, Rudolf / Ludwig Thuille (1908), Harmonielehre, Stuttgart: Carl Grünger.
Kruckenberg, Lori (1998), Art. »Sequenz«, in: Die Musik in Geschichte und Gegenwart, 2. Aufl. Kassel u.a. und Stuttgart: Bärenreiter und Metzler, Sachteil, Bd. 8, 1254–1286.
Moreno, Jaime (1993), Theoretical Reception of the Sequence and its Conceptual Implications, Ph.D. diss., Yale University 1993.
––– (2000), »Views of Sequential Repetition: From ›Satzlehre‹ to ›Melodielehre‹«, Journal of Music Theory 44, 127–169.
Mulder, Ernest W. (1947) Harmonie deel I: Theorie / Analyse, Utrecht: De Haan.
Piston, Walter (1940), Harmony, London: Gollancz.
Pfannkuch, Wilhelm (1998), Art. »Sequenz. (Satztechnischer Begriff)«, in: Die Musik in Geschichte und Gegenwart, 2. Aufl. Kassel u.a. und Stuttgart: Bärenreiter und Metzler, Sachteil, Bd. 8, 1286–1288.
Ricci, Adam (2002), »A Classification Scheme for Harmonic Sequences«, Theory and Practice 27, 1–36.
––– (2004), A Theory of the Harmonic Sequence, Ph.D. diss., University of Rochester, Eastman School of Music.
Taruskin, Richard (2005), The Oxford History of Western Music, Bd. 2: »The Seventeenth and Eighteenth Centuries«, Oxford: Oxford University Press.
Troschke, Michael von (1995), »Die Vernachlässigung von Sequenzmodellen in der traditionellen Harmonielehre«, in: Musica - Scientia et Ars: Eine Festgabe für Peter Förtig zum 60. Geburtstag, hg. von Günter Metz, Frankfurt am Main: Peter Lang, 29–37.
Dieser Text erscheint im Open Access und ist lizenziert unter einer Creative Commons Namensnennung 4.0 International Lizenz.
This is an open access article licensed under a Creative Commons Attribution 4.0 International License.